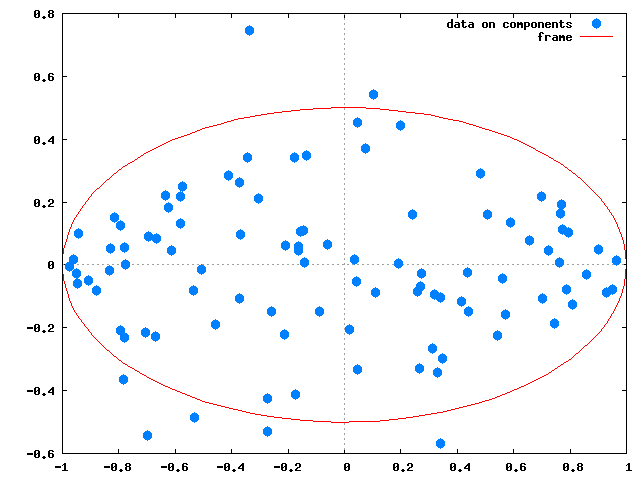
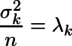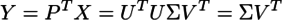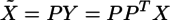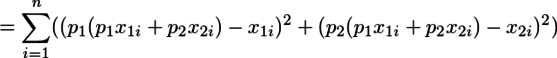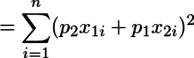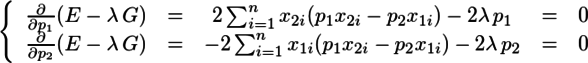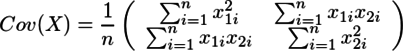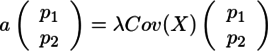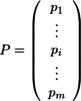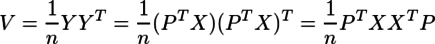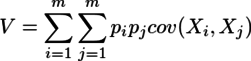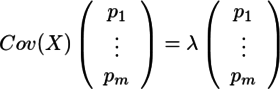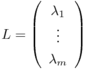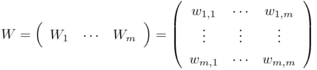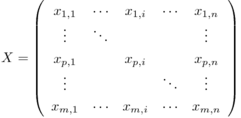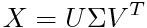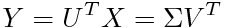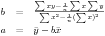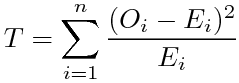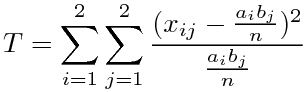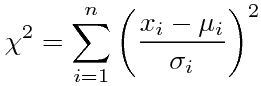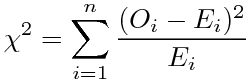分散分析というと、その名前自体によく「一元配置」「二元配置」とか「対応あり」「対応なし」とか「繰り返しのある」とか「繰り返しのない」とかいう言葉がついて回る。統計学の書籍でも、「一元配置分散分析」と「二元配置分散分析」は項目を分けて説明されることが多い。さらにそれぞれが「対応あり/なし」「繰り返しあり/なし」等で分けられると、目次に「分散分析」がたくさん並ぶことになる。Excelの「分析ツール」のメニューにも分散分析の項目があるが、
- 分散分析: 一元配置
- 分散分析: 繰り返しのある二元配置
- 分散分析: 繰り返しのない二元配置
などと分かれており、試しにやってみようと思っても、それらの違いがわからないとどうしようもない。同じ分散分析でも、それらの選択によっては、結果が的外れな意味を為さないものになる可能性があるのだ。その「分散分析」に付加される言葉の種類の多さに圧倒されて、分散分析は覚えることが多いと思って勉強する気を失ったのは、筆者だけであろうか。
筆者は未だに、どういう時にどの種類の分散分析を使うべきなのかよくわかっていない。
頭の中を整理するために、いつものように体当たり的に、
- 一元配置(対応なし)
- 一元配置(対応あり)
- 二元配置(繰り返しなし)
- 二元配置(繰り返しあり、対応なし)
- 二元配置(繰り返しあり、1要因対応あり)
- 二元配置(繰り返しあり、2要因対応あり)
のそれぞれの適用例を、筆者の職業に関係のあるソフトウェア開発を題材にして、考えてみることにした。
以下のデータは、全て架空のものである。
筆者はExcelを持っていないので、分散分析の計算にはRを使う。Rにも分散分析の関数はoneway.test(), aov(), anova(), lme()など色々あるが、今回は上記の全てをカバーできるaov()を使う。
最もシンプルな、一元配置(対応なし)の例として、次のようなデータを考える。
一元配置(対応なし)の例(1)
| 要因:モジュールの階層 |
|---|
| アプリ | ミドル | ドライバ |
|---|
生産性
(steps/人月) |
490
410
590
500
460
690
750
500
770
720
730
|
480
650
310
450
530
550
350
|
460
370
610
240
500
|
この生産性はモジュールの階層によって差があると言えるかどうか(差が無いなら滅多にこうはならないこと)を、分散分析で調べる。
> sample1 <- read.table("anova01.dat", header=TRUE)
> summary(aov(productivity ~ module, data=sample1))
Df Sum Sq Mean Sq F value Pr(>F)
module 2 120939 60470 3.5656 0.04738 *
Residuals 20 339182 16959
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
>
"Df"が自由度、"module"の行の"Sum Sq"が群間平方和(ここではモジュールの階層の違いによる効果)、"Mean Sq"が群間の不偏分散(モジュールの階層の違いによるばらつきの分散値)、Residuals(残差=群内のばらつき=全体に共通するはずのばらつき)の行のMean Sqが群内(全群共通)の不偏分散、"F value"が(群間/群内)の分散比、"Pr"(P値、そのF値以上が起こる確率)の右の'*'が有意水準0.05で有意であることを表す。
分散分析の帰無仮説は「全ての標本は同じ分布に従う母集団から得られたもの」→「各群の分布が同じであること」→「群間にばらつきがないこと」なので、分散比が有意であれば、「全体のばらつきに対して群間にばらつきがないとは言えない」、細かいことを言わなければ、群間にばらつきが認められ、各群の分布は同じでないことになる。
この例では、生産性はモジュールの階層によって違いがありそうということになる。
次の例は、同じ観測値を別の要因(観点)で分けたものである。
一元配置(対応なし)の例(2)
| 要因:所属 |
|---|
| A社 | B社 | C社 |
|---|
生産性
(steps/人月) |
490
410
460
590
500
370
460
690
|
750
480
500
650
770
|
610
310
720
450
530
240
550
350
730
500
|
> summary(aov(productivity ~ company, data=sample1))
Df Sum Sq Mean Sq F value Pr(>F)
company 2 68444 34222 1.7475 0.1998
Residuals 20 391677 19584
>
測定値が同じであることを明確にする為に、データファイルを同じsample1にしている。'*'のマークとその説明が出力されていないので、所属別では群間に有意な差が無く、このデータでは所属によって生産性にばらつきがあるとは言えないことになる。
もう1つ例を考えた。
一元配置(対応なし)の例(3)
| 要因:仕様書のファイル形式 |
|---|
| .doc | .txt | .xls | .ppt |
|---|
システムテスト
不具合数(/kstep) |
3
10
8
2
2
5
4
4
6
0
11
|
11
7
1
3
|
7
5
10
4
10
11
|
12
5
10
14
11
|
> sample2 <- read.table("anova02.dat", header=TRUE)
> summary(aov(error ~ format, data=sample2))
Df Sum Sq Mean Sq F value Pr(>F)
format 3 113.58 37.861 3.1192 0.04672 *
Residuals 22 267.03 12.138
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
このデータでは、システムテストで見つかったバグ数は、仕様書のファイル形式によって違いがありそうということになる。
測定データを一元配置分散分析(対応なし)する時のポイントを整理する。
- 測定値は正規分布することを仮定できるものであること
- 差があることを調べる群は、3群以上あること
(2群しか無いなら、その差をt検定するのと変わらない)
つまり、要因(群の分け方)はその水準(標本が属する群を決めるもの、値やID)が3つ以上あるように選ぶこと
- 各水準のデータ数は同じでなくても良い
- 水準はなるべく定量的な数値でないこと、数値であれば、なるべく測定値の従属変数でないことが明確であること
(要因と測定値に明確な関係があっても、群間のばらつきが十分に大きくないと有意差が検出できないため。また、水準(値の範囲)の取り方によって結果が変わってしまうため。例えば測定値と線形の関係にあるなら、無相関の検定をする方が良い)
最後の1点は、この記事を書くにあたって色々な例を考えてみた上での筆者の感想であり、そういうことを何かで読んだ記憶も無く、必ずしもそうではないかも知れない(温度の範囲などを水準に取る例も見かける)。
一元配置(対応あり)の例として、次のようなデータを考える。
各開発者がその4種類の開発プロセス(作業手順)を経験した時の、それぞれの開発プロセスにおける成績が、次のように得られたとする。
一元配置(対応あり)の例(1)
生産性
(steps/人月) | 要因:開発プロセス |
|---|
| Waterfall | Spiral | Incremental | TDD |
|---|
対
応
要
因
|
開発者A | 490 | 750 | 450 | 610 |
|---|
| 開発者B | 410 | 480 | 530 | 780 |
|---|
| 開発者C | 460 | 500 | 240 | 680 |
|---|
| 開発者D | 590 | 650 | 550 | 880 |
|---|
| 開発者E | 500 | 770 | 350 | 520 |
|---|
| 開発者F | 370 | 610 | 730 | 600 |
|---|
| 開発者G | 460 | 310 | 500 | 400 |
|---|
| 開発者H | 690 | 720 | 640 | 1030 |
|---|
Waterfallは要求分析、設計、実装、テストをこの順で1回ずつ行うやり方、Spiralは設計以降の作業を何回かに分けて設計、実装、テストを繰り返して積み上げ式に開発する方式、Incrementalは要求分析も含めて全体を繰り返す、1サイクル毎に一通り動くものができる機能追加方式、TDDは要求分析や設計をテストプログラム作成に代え、以降の作業はそのプログラムがOKを返すことだけを目的に行う、結果良ければ全て良し方式のことである。
開発者の能力や向き不向きには個人差があることを前提とし、それを計算に入れて、開発プロセスは生産性に影響するかどうかを、分散分析で調べる。
> sample3 <- read.table("anova03.dat", header=TRUE)
> summary(aov(productivity ~ process + Error(developer), data=sample3))
Error: developer
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 7 337872 48267
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
process 3 201184 67061 3.8348 0.02464 *
Residuals 21 367241 17488
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
"Error: developer"の部分は開発者の個人差による(開発者の違いを誤差要因とする)ばらつきに関するものであり、以降の計算はそれが除外されていることを示す。"Error: Within"の部分が、群内変動を誤差と見なして群間変動を検定するものである。
このデータでは、個人差の影響を差し引くと、開発プロセスは生産性に影響する要因と言えることになる。
もし、同じデータを「対応なし」として計算する(開発者の個人差を差し引かない)と、次のように、開発プロセス間に同じ有意差が出ない。
> summary(aov(productivity ~ process, data=sample3))
Df Sum Sq Mean Sq F value Pr(>F)
process 3 201184 67061 2.663 0.06729 .
Residuals 28 705112 25183
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
実際には各開発プロセスを短期間に経験することは難しく、開発者の経年変化や学習効果もあるので、こういうデータは取りにくいが、例えば開発者がソフトハウスのことであり、ソフトハウス内ではばらつきが無いと仮定すれば、各プロセスを同時に行うことも可能であるし、何より、筆者がこれ以上単純明快な例を思い付かないので、これで良しとする。
次の例は、会社による差(観測対象の個体差)はあるものとして、業務分野の違いが生産性に影響すると言えるかどうかを調べる。
一元配置(対応あり)の例(2)
生産性
(steps/人月) | 要因:開発分野 |
|---|
| 組み込み | 汎用 | 業務システム | ゲーム |
|---|
対
応
要
因
|
M社 | 330 | 470 | 450 | 320 |
|---|
| N社 | 290 | 440 | 370 | 630 |
|---|
| O社 | 450 | 550 | 580 | 750 |
|---|
| P社 | 320 | 360 | 470 | 460 |
|---|
| Q社 | 370 | 320 | 430 | 480 |
|---|
> sample4 <- read.table("anova04.dat", header=TRUE)
> summary(aov(performance ~ product + Error(company), data=sample4))
Error: company
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 4 102420 25605
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
product 3 80080 26693.3 4.0332 0.03379 *
Residuals 12 79420 6618.3
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
summary(aov(performance ~ product, data=sample4))
Df Sum Sq Mean Sq F value Pr(>F)
product 3 80080 26693 2.3487 0.1111
Residuals 16 181840 11365
1つ目のaov()が会社間に「対応あり」として計算した例、2つ目のaov()が「対応なし」として計算した例である。このデータだと、会社間の個体差を考慮に入れると、開発分野は生産性に影響する要因だったと言えることになる。
測定データを一元配置(対応あり)にする時のポイントを整理する。
- 群内の各測定値が、どの個体から得られた標本であるか(または、誤差要因のどの水準に属する標本であるか)がわかること
- 個体差によるばらつきはあるものとし、差し引いて考えるものであること
- 個体に有意差があるかどうかを調べる必要は無いこと
- 一部のデータが抜けていても計算可能
- 同水準、同個体のデータは1つでなく複数あっても計算可能(但し全てのセルのデータ数が同じであることが望ましい)
つまり、「対応あり」とは、異なる水準間(上の表の列間)でどれとどれが同じ個体から採取された(一般化すると、同じ誤差要因を持つ)標本であるかの対応が取れることである。
二元配置(繰り返しなし)の例として、次のようなデータを考える。
二元配置(繰り返しなし)の例(1)
生産性
(steps/人月) | 要因1:開発プロセス |
|---|
| Waterfall | Spiral | Incremental | TDD |
|---|
要因2:
座席の形態
| 大部屋 | 490 | 700 | 450 | 560 |
|---|
| 自由席 | 410 | 430 | 530 | 730 |
|---|
| パーティション | 460 | 450 | 240 | 630 |
|---|
| 小部屋 | 590 | 720 | 550 | 830 |
|---|
| 自宅 | 500 | 600 | 350 | 470 |
|---|
開発プロセスの違いも作業空間(座席の形態)の違いも生産性に影響し、それらの影響が足し合わせれていると仮定して、それぞれの組み合わせについて1つずつデータを採取し、2要因について同時に、その仮定が正しそうかどうかを調べる。
> sample5 <- read.table("anova05.dat", header=TRUE)
> summary(aov(productivity ~ process + workspace, data=sample5))
Df Sum Sq Mean Sq F value Pr(>F)
process 3 141255 47085 4.8533 0.01951 *
workspace 4 121420 30355 3.1288 0.05589 .
Residuals 12 116420 9702
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
よって、このデータでは、開発プロセスの違いによる効果は有意水準0.05で有意差あり、作業空間の違いによる効果は有意差なし(有意水準が0.1だと有意差あり)となる。
ちなみに、開発プロセスと作業空間についてそれぞれ、同じデータを一元配置とみなして計算すると、次のように、同じ水準の有意差は出ない。
> summary(aov(productivity ~ process, data=sample5))
Df Sum Sq Mean Sq F value Pr(>F)
process 3 141255 47085 3.1675 0.05318 .
Residuals 16 237840 14865
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> summary(aov(productivity ~ workspace, data=sample5))
Df Sum Sq Mean Sq F value Pr(>F)
workspace 4 121420 30355 1.7671 0.188
Residuals 15 257675 17178
このデータの特徴は、全体のばらつきを、2つの要因のばらつきと共通のばらつきの3つに分解するからこそ、明確になるのである。
次の例は、何らかの開発成果物の欠陥数を、作業期間と納入した曜日との組み合わせのそれぞれについて1つずつ、データを採取したとするものである。
二元配置(繰り返しなし)の例(2)
欠陥数
/kstep |
要因1:開発期間 |
| 1週間 | 2週間 | 1ヶ月 |
|---|
要因2:
曜日
| 月曜 | 10 | 6 | 4 |
|---|
| 火曜 | 6 | 9 | 6 |
|---|
| 水曜 | 8 | 6 | 4 |
|---|
| 木曜 | 4 | 9 | 4 |
|---|
| 金曜 | 8 | 6 | 4 |
|---|
| 土曜 | 10 | 9 | 9 |
|---|
| 日曜 | N/A | 6 | 9 |
|---|
> sample6 <- read.table("anova06.dat", header=TRUE)
> summary(aov(error ~ time_limit + delivery, data=sample6))
Df Sum Sq Mean Sq F value Pr(>F)
time_limit 2 14.360 7.1798 2.8898 0.09803 .
delivery 6 48.861 8.1435 3.2777 0.04224 *
Residuals 11 27.329 2.4845
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1 observation deleted due to missingness
> summary(aov(error ~ delivery, data=sample6))
Df Sum Sq Mean Sq F value Pr(>F)
delivery 6 51.217 8.5361 2.8213 0.05523 .
Residuals 13 39.333 3.0256
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1 observation deleted due to missingness
よって、このデータでは、開発期間の違いによる差も考慮すると、納品日の曜日によって有意水準0.05で有意な差があるという結果になる。
2つ目のaov()は、上の例と同様、一元配置では同じ有意差が出ないことを確認したものである。
二元配置(繰り返しなし)にする時のポイントを整理する。
- 2つの要因の全ての水準の組み合わせについて、データは1つ
- どちらの要因も何らか影響していると思われ、それぞれの影響を分離して調べようとしていること
- 一部のデータが抜けていても計算可能
- 一元配置(対応あり、繰り返しなし)の代用として行うことも可能
表の形が同じことからもわかるように、一元配置(対応あり)と二元配置は計算方法が同じであり、一元配置の対応を決める要因についてのF検定を省くかどうかが異なるだけである。
Excelの分析ツールに「対応のある一元配置」が無いのは、二元配置で代用できるからだろう。
二元配置(繰り返しあり、対応なし)は、表の形としては、繰り返しのない二元配置の各セルに複数のデータが含まれるだけの違いなので、同じような要因のペアが使える。
二元配置(繰り返しあり、対応なし)の例(1)
生産性
(steps/人月) | 要因1:開発プロセス |
|---|
| Waterfall | Spiral | Incremental | TDD |
|---|
要因2:
座席の形態
| 大部屋 |
570
660
450 |
710
480
570 |
570
450
620 |
520
540
740 |
|---|
| 自由席 |
570
500
270 |
590
460
670 |
510
450
410 |
620
350
350 |
|---|
| パーティション |
300
480
580 |
670
500
710 |
610
540
540 |
430
650
600 |
|---|
| 小部屋 |
510
530
530 |
660
620
510 |
310
550
780 |
760
400
590 |
|---|
| 自宅 |
510
560
530 |
570
750
590 |
400
380
520 |
600
610
580 |
|---|
繰り返しがある(同じセルに複数のデータがある)と、行の効果、列の効果に加えて、交互作用の効果を分離して計算することが可能で、交互作用を分けるか分けないかで計算結果が変わる。
交互作用とは、2要因の水準の特定の組み合わせにだけに影響する効果のことで、例えばその行とその列は大体高い値なのにそのセルだけやたら低い値が多いということを起こす要因である。
aov()で交互作用を分離して分散分析するには、引数において2つの要因を'*'で繋ぐ。
> sample7 <- read.table("anova07.dat", header=TRUE)
> summary(aov(productivity ~ process * workspace, data=sample7));
Df Sum Sq Mean Sq F value Pr(>F)
process 3 98952 32984 2.4676 0.07599 .
workspace 4 65823 16456 1.2311 0.31308
process:workspace 12 69657 5805 0.4343 0.93963
Residuals 40 534667 13367
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
"process:workspace"の行が交互作用に関する行で、このデータでは有意差は出なかった。また、交互作用を分離すると、開発プロセスにも作業空間にも有意水準0.05の有意差はなしである。
交互作用を分離せずに計算するには、aov()の引数において、2つの要因を'+'で繋ぐ。
> summary(aov(productivity ~ process + workspace, data=sample7));
Df Sum Sq Mean Sq F value Pr(>F)
process 3 98952 32984 2.8382 0.04686 *
workspace 4 65823 16456 1.4160 0.24170
Residuals 52 604323 11622
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
このデータでは、交互作用を分離しなければ、開発プロセスには有意差が認められる(交互作用の効果を分離しない方が有意差が出る)ことがわかる。
ちなみに、繰り返しがないと、'+'でも'*'でも結果は変わらない。
もう1つ例を作る。
二元配置(繰り返しあり、対応なし)の例(2)
結合テストエラー数
/kstep |
要因1:仕様書の配布形態 |
|---|
| Word | Excel | PDF | HTML |
|---|
要因2:
設計書の
フォーマット
| Word |
8
6
2
1
7 |
5
7
3
9
10 |
4
11
5
6
3 |
11
7
14
7
9 |
|---|
| Excel |
11
5
8
13
8 |
4
10
6
3
6 |
5
9
13
6
10 |
17
12
11
5
10 |
|---|
| Text |
5
6
6
10
11 |
6
12
7
9
8 |
5
12
8
9
6 |
9
8
13
11
3 |
|---|
| HTML |
12
14
7
13
12 |
10
15
6
13
13 |
12
7
5
13
7 |
4
10
3
8
9 |
|---|
> sample8 <- read.table("anova08.dat", header=TRUE)
> summary(aov(error ~ given_spec * design_desc, data=sample8))
Df Sum Sq Mean Sq F value Pr(>F)
given_spec 3 86.5 28.8333 2.9254 0.04043 *
design_desc 3 17.1 5.7000 0.5783 0.63137
given_spec:design_desc 9 198.4 22.0444 2.2366 0.03056 *
Residuals 64 630.8 9.8562
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
> summary(aov(error ~ given_spec + design_desc, data=sample8))
Df Sum Sq Mean Sq F value Pr(>F)
given_spec 3 86.5 28.833 2.5384 0.06314 .
design_desc 3 17.1 5.700 0.5018 0.68221
Residuals 73 829.2 11.359
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
1つ目のaov()の結果より、このデータでは仕様書のフォーマットが欠陥数に影響しており、また設計書のフォーマットとの交互作用もある結果となった。
2つ目のaov()の結果は、交互作用を分離しないと、仕様書のフォーマットについても同じ有意差は出ない(1つ前のデータ例とは逆に、交互作用を分離する方が有意差が出る)ことを示している。
二元配置(繰り返しあり、対応なし)にする時のポイントを整理する。
- 2つの要因の全ての水準の組み合わせについて、複数のデータがある
- それにより、2つの要因の交互作用が混入する
- 交互作用によるばらつきを分離して計算するかどうかは場合による
- 一元配置(対応あり、繰り返しあり)の代用として行うことも可能
一元配置(対応あり)を代用する時に交互作用をどう扱うかが問題になるが、誤差要因と何かの交互作用というのはやはり誤差要因だと考えるなら、交互作用を分離して、誤差要因も交互作用も検定から除外する(aov()なら'*'を使った上で検定中の要因そのもの以外の行を無視する)のが好ましいと思う。
「二元配置(1要因対応あり)」は、「対応のある要因と対応のない要因の二元配置」と書かれることが多いようだが、そう書かれると余計にややこしく見えるのは、筆者だけだろうか。
「対応あり」とは、一元配置の場合と同様、繰り返しのある(セル内に複数ある)データのそれぞれが、他の水準(セル)のどのデータに対応するかがわかる、という意味であり、対応を取るからには、個体差の影響を取り除いて計算する必要があると考えていることになる。
1要因についてのみ対応が取れる状況として、次のような例を考える。
二元配置(繰り返しあり、1要因対応あり)の例(1)
生産性
(steps/人月) | 要因1:開発プロセス |
|---|
| Waterfall | Spiral | Incremental | TDD |
|---|
要因2:
座席の形態
+ 人
| 作業場 | 開発者 |
|---|
| 大部屋 |
A | 630 | 660 | 570 | 340 |
|---|
| B | 530 | 430 | 430 | 400 |
|---|
| C | 390 | 640 | 520 | 530 |
|---|
| パーティション |
D | 400 | 760 | 500 | 680 |
|---|
| E | 550 | 670 | 290 | 890 |
|---|
| F | 650 | 620 | 280 | 820 |
|---|
| 小部屋 |
G | 470 | 680 | 760 | 410 |
|---|
| H | 530 | 580 | 670 | 930 |
|---|
| I | 850 | 980 | 790 | 980 |
|---|
| 自宅 |
J | 610 | 850 | 530 | 310 |
|---|
| K | 400 | 640 | 230 | 400 |
|---|
| L | 530 | 430 | 470 | 330 |
|---|
開発者間には能力の個人差があるのは普通だから、開発者の違いは、標本の対応を取ってその影響を除外して計算するにふさわしい、誤差要因であろう。
前記のように同じ人が4つの開発プロセスを経験するというのは現実的に多少無理があるが、それはなされたとする。
全ての開発者がこれらの全ての作業空間を経験するのは現実的に不可能であろう。と思うので、そういう席替えはなされず、作業場毎に別の人を選んでデータを採取したとする。
つまり、開発プロセスについては、水準間でどれとどれが同じ人のデータであるかの対応があり、作業空間に関しては、水準間でそういう対応がない、というデータである。
> sample9 <- read.table("anova09.dat", header=TRUE)
> summary(aov(productivity ~ process * workspace + Error(developer), data=sample9))
Error: developer
Df Sum Sq Mean Sq F value Pr(>F)
workspace 3 424492 141497 3.8251 0.05734 .
Residuals 8 295933 36992
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
process 3 163692 54564 3.0262 0.04914 *
process:workspace 9 391275 43475 2.4112 0.04123 *
Residuals 24 432733 18031
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
このように、開発プロセスの違いによる影響には有意差があり、また開発プロセスと作業空間の間には何らかの交互作用があるという結果になった。
もし同じデータを対応なしの二元配置として計算すると、次のように全く異なる結果になる。
> summary(aov(productivity ~ process * workspace, data=sample9))
Df Sum Sq Mean Sq F value Pr(>F)
process 3 163692 54564 2.3962 0.086440 .
workspace 3 424492 141497 6.2140 0.001898 **
process:workspace 9 391275 43475 1.9092 0.086483 .
Residuals 32 728667 22771
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
これは、データをよく見るとわかるのだが、小部屋に飛び抜けて成績が良い人が居ることに起因しており、作業空間の違いによる効果だと言うにはかなり不適切であろう。
1要因にのみ対応がある例としてもう1つ、次のようなデータを考える。
開発者A〜Fで構成されるグループが、6つの分野の業務を行った時の生産性を測ったという例である。
二元配置(繰り返しあり、1要因対応あり)の例(2)
生産性
(steps/人月) |
要因1:性別 + 人 |
|---|
| 性別 | 男性 | 女性 |
|---|
| 開発者 | A | B | C | D | E | F |
|---|
要因2:
業務分野
| 組み込み(アプリ) |
470 | 720 | 550 | 610 | 580 | 550 |
|---|
| 業務システム |
490 | 530 | 530 | 570 | 310 | 380 |
|---|
| 生産システム |
530 | 520 | 570 | 600 | 520 | 490 |
|---|
| PCアプリ |
530 | 310 | 460 | 420 | 690 | 650 |
|---|
| Javaアプリ |
600 | 530 | 500 | 450 | 790 | 590 |
|---|
| ゲーム機ソフト |
450 | 530 | 400 | 530 | 350 | 530 |
|---|
上の例では対応を決める要因を縦に並べたが、今度は横に並べた。
開発者の能力には当然個人差がある。
全開発者が6つの分野にて仕事をしたので、分野間ではどれとどれが同じ人のデータであるかの対応が取れる。
1人の開発者は男性と女性の両方を経験できないので、男性群と女性群のデータには対応が取れない。
> sample10 <- read.table("anova10.dat", header=TRUE)
> summary(aov(productivity ~ sex * area - Error(developer), data=sample10))
Error: developer
Df Sum Sq Mean Sq F value Pr(>F)
sex 1 4225.0 4225.0 9.6266 0.03613 *
Residuals 4 1755.6 438.9
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: Within
Df Sum Sq Mean Sq F value Pr(>F)
area 5 77314 15463 1.2919 0.3066
sex:area 5 51892 10378 0.8671 0.5202
Residuals 20 239378 11969
> summary(aov(productivity ~ sex * area, data=sample10))
Df Sum Sq Mean Sq F value Pr(>F)
sex 1 4225 4225 0.4205 0.5228
area 5 77314 15463 1.5390 0.2153
sex:area 5 51892 10378 1.0330 0.4209
Residuals 24 241133 10047
1つ目のaov()の出力より、このデータでは、性別による影響に有意差が見られるという結果になる。
2つ目のaov()の出力は、2要因とも対応なしとして計算すると、どの要因、交互作用にも有意差が見られないことを示すものである。
二元配置(1要因のみ対応あり)にする時のポイントを整理する。
- 標本には個体差があることを前提とする
- 1つの要因については、複数の水準に同じ個体からの標本があり、水準間でデータの対応が取れる
例えば、同じ被験者から、各水準の条件下でデータが取られている
- もう1つの要因については、1つの個体からの標本は1つの水準にしかなく、水準間でデータに対応がない
例えば、水準を決める条件は同時に発生するので、水準毎に異なる被験者を選ぶ
もちろん、対応を決める要因は、個人や個体に限らず、標本に影響があることが既にわかっている条件であれば何でも良い。
二元配置(2要因対応あり)の標本のデータ構造は、1要因のみ対応ありのものよりも単純である。
二元配置(繰り返しあり、2要因対応あり)の例(1)
欠陥数
(steps/人月) | 要因1:開発プロセス |
|---|
| Waterfall | Spiral | Incremental | TDD |
|---|
要因2:
座席の形態
+ フェーズ
|
作業空間 | 開発フェーズ |
|---|
| 大部屋 |
仕様作成 | 6 | 6 | 7 | 3 |
|---|
| 全体設計 | 4 | 7 | 8 | 7 |
|---|
| 個別設計 | 6 | 8 | 10 | 5 |
|---|
| テスト設計 | 3 | 2 | 6 | 4 |
|---|
| 実装 | 6 | 5 | 8 | 8 |
|---|
| 小部屋 |
仕様作成 | 2 | 6 | 3 | 5 |
|---|
| 全体設計 | 5 | 7 | 4 | 6 |
|---|
| 個別設計 | 6 | 3 | 10 | 4 |
|---|
| テスト設計 | 7 | 5 | 6 | 4 |
|---|
| 実装 | 12 | 5 | 6 | 7 |
|---|
| 自宅 |
仕様作成 | 5 | 4 | 9 | 4 |
|---|
| 全体設計 | 9 | 2 | 9 | 6 |
|---|
| 個別設計 | 7 | 9 | 9 | 7 |
|---|
| テスト設計 | 5 | 3 | 3 | 2 |
|---|
| 実装 | 4 | 9 | 10 | 11 |
|---|
要するに3次元なのである。ここでは表を立体的に書けないので、対応を決める「開発フェーズ」については列方向に展開している。
開発フェーズが違うと仕事の性質が全く違うので、フェーズの違いは当然ミスの数に影響する。
どんな開発プロセスにも、これくらいのフェーズは存在するので、各フェーズのデータはあり得る。また、どんな作業空間でも、一通りの開発をすれば全てのフェーズを経るので、各フェーズのデータが得られる。従って、異なる開発プロセスのデータ間でも異なる作業空間のデータ間でも、フェーズの違いによる対応が取れる。
> sample11 <- read.table("anova11.dat", header=TRUE)
> summary(aov(error ~ process * workspace - Error(phase/(process*workspace)), data=sample11))
Error: phase
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 4 94.733 23.683
Error: phase:process
Df Sum Sq Mean Sq F value Pr(>F)
process 3 30.850 10.2833 3.8482 0.03852 *
Residuals 12 32.067 2.6722
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: phase:workspace
Df Sum Sq Mean Sq F value Pr(>F)
workspace 2 4.9333 2.4667 0.6251 0.5594
Residuals 8 31.5667 3.9458
Error: phase:process:workspace
Df Sum Sq Mean Sq F value Pr(>F)
process:workspace 6 17.20 2.8667 0.5148 0.7912
Residuals 24 133.63 5.5681
2要因対応ありのデータ構造は単純だが、その計算は、コンピューター任せでも複雑である。対応を決める要因の違いによる影響が、要因1との交互作用、要因2との交互作用、要因1と要因2と対応要因との交互作用と多岐に渡って分離して計算されるからである。
上記のaov()の構造式のError()の部分は、その構造がわかりやすいように
- Error(phase + phase/process + phase/workspace)
- Error(phase + phase:process + phase:workspace)
- Error(phase + phase:process + phase:workspace + phase:process:workspace)
といった形で書かれることも多いようだが、ここではシンプルで入力ミスも避けられる
- Error(phase / (process * workspace))
を採用している。
上の計算結果では開発プロセス間に有意差が出たが、同じデータを対応なしとして計算すると、次のようにどこにも有意差が出ない。
> summary(aov(error ~ process * workspace, data=sample11))
Df Sum Sq Mean Sq F value Pr(>F)
process 3 30.850 10.2833 1.6904 0.1816
workspace 2 4.933 2.4667 0.4055 0.6689
process:workspace 6 17.200 2.8667 0.4712 0.8262
Residuals 48 292.000 6.0833
もう1つ例を考える。新規に参入した人がそこの設計業務をマスターするのに何ヶ月かかったかというデータが、次のように得られたとする。
二元配置(繰り返しあり、2要因対応あり)の例(2)
定着期間
(ヶ月) | 要因1:設計手法 |
|---|
| 構造化設計 | データ指向 | オブジェクト指向 | コンポーネント指向 |
|---|
要因2:
開発内容
+ 性別
|
開発内容 | 性別 |
|---|
| プラットフォーム |
男性 | 8 | 9 | 7 | 11 |
|---|
| 女性 | 3 | 6 | 7 | 7 |
|---|
| ミドルウェア |
男性 | 2 | 4 | 3 | 6 |
|---|
| 女性 | 9 | 5 | 9 | 8 |
|---|
| フレームワーク |
男性 | 10 | 9 | 10 | 9 |
|---|
| 女性 | 9 | 10 | 5 | 11 |
|---|
| アプリケーション |
男性 | 11 | 9 | 5 | 5 |
|---|
| 女性 | 12 | 10 | 1 | 5 |
|---|
男性と女性とでは元々差があるはずだという前提で、対応ありの分散分析を行う。
> sample12 <- read.table("anova12.dat", header=TRUE)
> summary(aov(takes_month ~ design_policy * target - Error(gender/(design_policy*target)), data=sample12))
Error: gender
Df Sum Sq Mean Sq F value Pr(>F)
Residuals 1 0.03125 0.03125
Error: gender:design_policy
Df Sum Sq Mean Sq F value Pr(>F)
design_policy 3 23.3438 7.7813 14.647 0.0269 *
Residuals 3 1.5938 0.5313
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Error: gender:target
Df Sum Sq Mean Sq F value Pr(>F)
target 3 45.844 15.281 0.8886 0.5375
Residuals 3 51.594 17.198
Error: gender:design_policy:target
Df Sum Sq Mean Sq F value Pr(>F)
design_policy:target 9 95.531 10.6146 2.3142 0.1136
Residuals 9 41.281 4.5868
> summary(aov(takes_month ~ design_policy, data=sample12))
Df Sum Sq Mean Sq F value Pr(>F)
design_policy 3 23.344 7.7812 0.9237 0.4422
Residuals 28 235.875 8.4241
このデータでは、男女の違いによる対応ありとすると、設計手法の違いによる有意差が見られ、対応なしとすると、設計手法にも開発内容にもその違いによる差が見られないという結果になった。



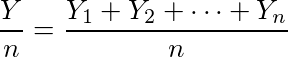
![\lim_{n\to\infty} \frac{Y}{n} = E[Y_1] = 1](/archives/images/ftochi2-08.png)

 ...(1)
...(1)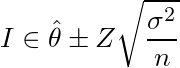
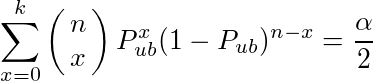

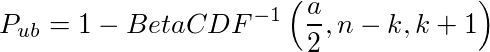
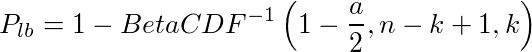
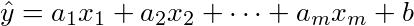
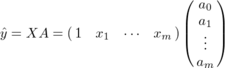





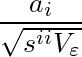




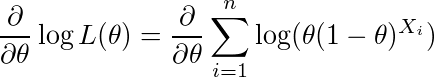
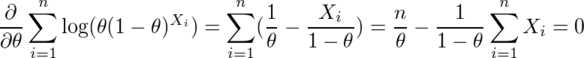
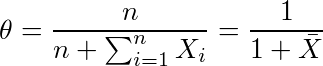
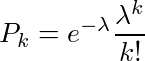
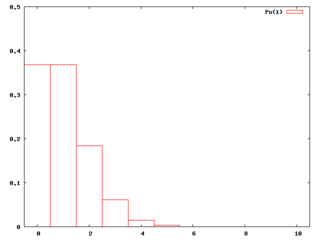

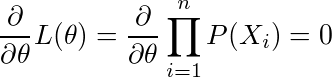
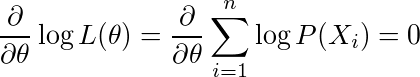


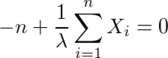
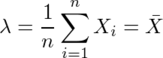
 (または不等号を逆にして=1)
(または不等号を逆にして=1)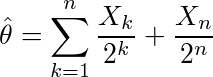
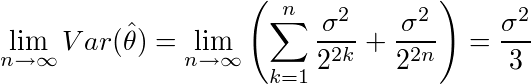
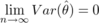 となり、θ^はθに限りなく近づく)
となり、θ^はθに限りなく近づく)![Var(¥hat{¥theta}) ¥geq ¥frac{1}{n E¥left¥{¥left[¥frac{¥partial}{¥partial¥theta}¥log P(X)¥right]^2¥right¥}} ¥equiv ¥sigma_0^2](/archives/images/cramer-rao1.png)

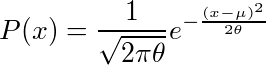
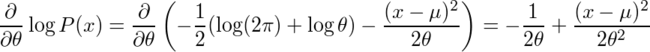


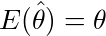 ...(1)
...(1) 。学生時代にこのθの上の屋根の意味が理解できなかったことが、私が推定・検定の1手目でつまずいた原因の1つであることは間違いない。そもそもなぜ統計学では推定するパラメーターをθと書くのか。高校の三角関数の授業で習って以来、私にとってはθといえば角度に違いないのであり、パラメーターをθと表すのは、円周率をxと表すとか、y=ax+bのxとyが定数でaとbがグラフの縦軸・横軸であるくらいの混乱の元である。
。学生時代にこのθの上の屋根の意味が理解できなかったことが、私が推定・検定の1手目でつまずいた原因の1つであることは間違いない。そもそもなぜ統計学では推定するパラメーターをθと書くのか。高校の三角関数の授業で習って以来、私にとってはθといえば角度に違いないのであり、パラメーターをθと表すのは、円周率をxと表すとか、y=ax+bのxとyが定数でaとbがグラフの縦軸・横軸であるくらいの混乱の元である。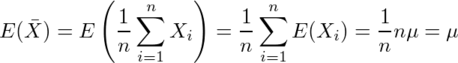
 、不偏分散
、不偏分散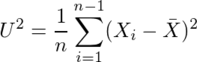 がσ2の不偏推定量かどうかを考える。
がσ2の不偏推定量かどうかを考える。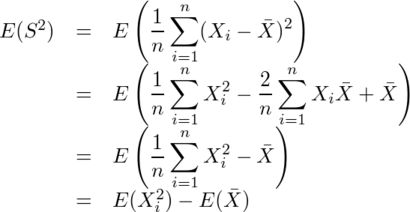
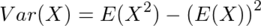 の公式と
の公式と の公式を用いると、
の公式を用いると、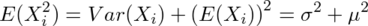


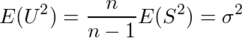



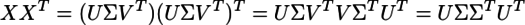 ...(1)
...(1)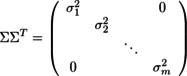 ...(2)
...(2)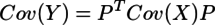
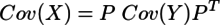
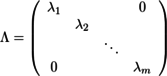
 ...(3)
...(3)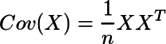
 ...(4)
...(4) すなわち
すなわち