統計学復習メモ17: 重回帰分析の計算結果の検定

以前に回帰直線を求めることと主成分分析は似ていると書いたが、ちょっと無理があり過ぎたかも知れない。なぜか主成分分析が因子分析より知名度が低いのが気に入らなくて、メジャーなものと結びつけたくて書いたのだが、やっぱり回帰分析と主成分分析は全然違う。回帰分析は目的変数を説明変数で説明しようとするものであり、主成分分析はデータの傾向を見るものである。通常、回帰直線を求める際に最小にする誤差は目的変数軸上の誤差であるが、第一主成分を求める為に最小にする誤差は全変数が構成する空間での誤差である。
筆者は、主成分分析は多変量解析の基本かつ最も重要であると考えており、学生時代には趣味のプログラミングのネタにするほど惚れ込んだが、因子分析はあまり好みでないのである。暴走ついでにさらに暴走すると、筆者の中では、

A群B群C群
因子分析主成分分析回帰分析
LinuxFreeBSDOpenBSD
RubyPythonPerl
WindowsMacUNIX
SleipnirLunascapeFirefox
秀丸サクラエディタEmacs
のような関係があり、因子分析は軟派で軽薄でチャラいのである。


閑話休題。今回は重回帰分析を復習する。一次回帰直線が、xを説明変数、yを目的変数とし、直線y^=a x+bの係数aと切片bをデータから求めたものだとすると、重回帰分析はそのxを複数次元にしたもの、
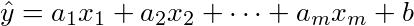
¥hat{y}=a_1x_1+a_2x_2+¥cdots+a_mx_m+b
の係数aiとy切片bを求めるものである。
便宜上、上のbをa0と書き、
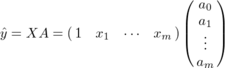
¥hat{y}=XA=¥pmatrix{1 & x_1 & ¥cdots & x_m}¥pmatrix{a_0 ¥cr a_1 ¥cr ¥vdots ¥cr a_m}
と行列の積で表すことにする。

n個のデータの組(yi, x1i, x2i, x3i, ...)(1<=i<=m)が得られた時、誤差をeiとすると、

である。以下、これをY=XA+Eと書く。
yの誤差eiの２乗和が最小になるようにAを求めるとすると、
¥sum_{i=1}^{n}e_i^2=E^TE=(Y-XA)^T(Y-XA)
であり、これはaiの２次関数なので、これを偏微分して0になるAが答であるから、
¥frac{¥partial}{¥partial A}(E^TE)=¥frac{¥partial}{¥partial A}(Y^TY-2(XA)^TY-(XA)^TXA)=-2X^TY+2X^TXA=0
なので
A=(X^TX)^{-1}X^TY
という計算で求められることがわかる。(XTX)が正則でないと逆行列が存在しないという問題はあるが、異なるデータの個数が説明変数の数より少ないとか、中身が0だらけのぜろりとしたデータでない限りは正則だろうから、とりあえず気にしないことにする。

試しに次のサンプルデータのバグ数について計算してみる。

部品バグ数開発規模関係者数疲労度
A70.935
B152.118
C101.249
D71.217
E60.359
F50.693
G70.922
H50.363
I60.358
J70.634
これを"bugs.dat"というタブ区切りのテキストファイルにして、Maximaで 
dat:read_matrix("bugs.dat");
n:10$ /*標本数*/
p:3$ /*説明変数の数*/
Y:submatrix(dat,2,3,4); /*1列目を取り出す（2-4列目を除去）*/
X1:submatrix(dat,1); /*2列目以降を取り出す（1列目を除去）*/
X:map(lambda([x],append([1],x)),X1); /*X1の左端に要素が全て1の列を追加*/
A:invert(transpose(X).X).transpose(X).Y; /*回帰係数*/
fpprintprec:4$
float(A);
を実行すると、次の結果が得られる。
a02.1
a14.612
a20.02896
a30.2436
バグ数=2.1 + 4.612*開発規模 + 0.02896*関係者数 + 0.2436*疲労度、という意味である。
この結果がどれくらい元データに合ってるかを、Yの値で見てみる。 
/*元データ、回帰式による推定値、誤差*/
[Y, X.A, Y-X.A];
元データYYの推定値Y^Y-Y^
77.556-.5558
1513.761.237
109.943.05743
79.369-2.369
65.8210.179
55.859-.8589
76.7960.204
54.388.6115
65.577.4226
75.9291.071

YとY^が十分近いので、これでも満足なのだが、統計学にはこの回帰分析結果をきちんと検定する方法が存在するようである。
その前に一応、よくある指標を計算する。以下、データ数をn、説明変数の数をpとする。

load(descriptive)
load(distrib)
n:10$
p:3$
/*重相関*/
R:cor(addcol(Y,X.A)),numer;
/*決定係数（寄与率）*/
R^2;
/*自由度補正済み決定係数*/
1-(1-R[1,2]^2)*(n-1)/(n-p-1);
重相関0.9361
決定係数0.8762
自由度修正決定係数0.8143
相関係数の類は、値の解釈が難しいので、相関係数同士を比較する以外には使いづらい。一応、自由度修正済み決定係数が0.8以上というのがよく使われる基準であるらしい。
これは置いといて、まず、回帰式全体の有効性を検定する。これには、回帰分散÷残差分散、
¥frac{V_{¥hat{y}}}{V_¥varepsilon}=¥frac{¥frac{1}{p}¥sum_{i=1}^{n}(¥hat{y}_i-¥bar{y})^2}{¥frac{1}{n-p-1}¥sum_{i=1}^{n}(¥hat{y}_i-y_i)^2}
という値が自由度p,n-p-1のF分布に従う、というのが使えるらしい。YとY^の誤差の分散が十分に小さいかどうかを調べようとするものと言えるだろう。 
E: Y-X.A$
/*回帰分散*/
Y_hat: X.A-mean(Y)[1]$
Vy: transpose(Y_hat).Y_hat/p,numer;
/*残差分散*/
Ve: transpose(E).E/(n-p-1);
/*回帰方程式のF値*/
f:Vy/Ve;
/*そのF値以上の発生確率*/
1-cdf_f(f,p,n-p-1);
結果
F値14.16
P(F(3,6)>14.16)0.03951
有意水準を0.05とすると、回帰分散＝残差分散という仮説は棄却されるので、この回帰式は有効ということになる。

次に、回帰係数aiそれぞれの有効性を検定する。これには、回帰係数÷標準誤差＝
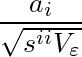
¥frac{a_i}{¥sqrt{s^{ii}V_{¥varepsilon}}}
（sijは共変動行列（＝ｎ×共分散行列）の逆行列の要素）
という値が自由度n-p-1のｔ分布に従う、というのを使う。定数項a0については、siiの部分は次のような式になるが、同じようにｔ値が求められる。
s^{00}=¥frac{1}{n}+¥sum_{i=1}^{p}¥sum_{j=1}^{p}¥bar{X_i}¥bar{X_j}s^{ij}

/*共変動行列の逆行列*/
Sinv: invert(cov(X1)*n);
/*標準誤差（係数項）*/
Se[i]:=sqrt(Sinv[i,i]*Ve);
/*標準誤差（定数項）*/
Se[0]:sqrt((1/n + sum(sum(mean(X1)[i]*mean(X1)[j]*Sinv[i,j],j,1,p),i,1,p))*Ve);
for i:0 thru 3 do print(Se[i])$
iaiの標準誤差
01.863
11.023
20.2303
30.1661
/*回帰係数のt値、|t|値がそれより大きい確率*/
t[i]:=A[i+1,1]/Se[i]$
for i:0 thru 3 do print(t[i], 2*(1-cdf_student_t(t[i],n-p-1)))$
iｔ値確率
01.1280.3025
14.5070.004074
20.12570.904
31.4670.1928
有意水準を0.05とすると、a1についてのみ、本当は0である（係数に意味が無い）という仮説が棄却され、有効ということになる。

もちろん、以上のような計算は、R（フリーの統計処理ソフト）やExcelを使うと一発である。
Rで計算すると、次のようになる。（先頭が">"の行が入力部分）
> data1 <- read.table("bugs.dat")
> X <- data.frame(data1[2:4])
> Y <- data1[,1,drop=TRUE]
> summary(lm(Y~.,X))

Call:
lm(formula = Y ~ ., data = X)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.3685 -0.4025  0.1915  0.5643  1.2374 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept)  2.10044    1.86263   1.128  0.30252   
V2           4.61167    1.02326   4.507  0.00407 **
V3           0.02896    0.23034   0.126  0.90404   
V4           0.24358    0.16607   1.467  0.19281   
---

Residual standard error: 1.289 on 6 degrees of freedom
Multiple R-squared: 0.8762,	Adjusted R-squared: 0.8143 
F-statistic: 14.16 on 3 and 6 DF,  p-value: 0.003951

もちろん、今回のMaximaによる計算は、先にRによる結果があって、同じものが得られるようにがんばったものである。こんなに大変だとは思わなかった。

どうでもいいが、筆者はA群に書いたLinuxやWindowsを使わない訳ではない。どちらかというと硬派で右翼なB群の方が好きというだけのことで、筆者もA群の方にはるかに恩恵を受けている。A群とB群の棲み分けは必要だと思うし、筆者のような人間のために、ぜひそういう特徴は損なわれないで頂きたいものである。
因子分析は、主成分分析と同じ計算方法を用いることもあるなど、手段を選ばない所があると思うので、筆者としてはA群なのである。


（2010/10/24追記）s00の導出方法
標本の説明変数側が

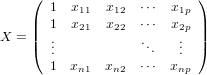
の時（xijのiとjを上記のものと逆に書いているが同じ意味）、定数項以外の平均が0になるように平行移動して
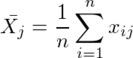
\bar{X_j}=\frac{1}{n}\sum_{i=1}^{n}x_{ij}

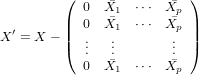
とすると、X'と共変動行列Sijとの間に
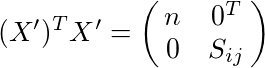(X')^TX'=\pmatrix{n & 0^T \cr 0 & S_{ij}}...(1)
((X')^TX')^{-1}=\pmatrix{n^{-1} & 0^T \cr 0 & S_{ij}^{-1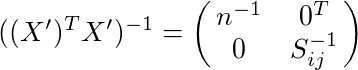}}...(1')
というのが成り立つようになる。これを使って、Var(A)を計算する。
上記と同様に、YとX'A'との誤差の２乗和が最小になるような回帰係数A'について、「正規方程式」
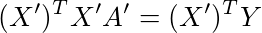(X')^TX'A'=(X')^TY...(2)
が成り立つ。このA'は定数項以外の成分はAと同じなので、
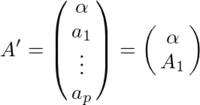
A'=\pmatrix{\alpha \cr a_1 \cr \vdots \cr a_p}=\pmatrix{\alpha \cr A_1}
と書くことにすると、(2)は(1)を使って
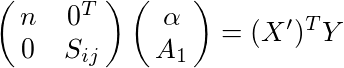
\pmatrix{n & 0^T \cr 0 & S_{ij}}A'=(X')^TY
と書き換えることができ、
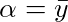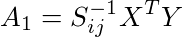
\alpha=\bar{y}と A_1=S_{ij}^{-1}X^TY
がわかる。

これ以降、推定量を表す変数には^を付ける。これまでのAはA^であり、以降のAは母集団の回帰係数である。
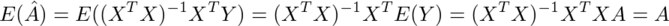
E(\hat{A})=E((X^TX)^{-1}X^TY)=(X^TX)^{-1}X^TE(Y)=(X^TX)^{-1}X^TXA=A
であることからA^がAの不偏推定量であることがわかり、
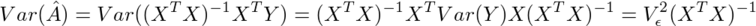
Var(\hat{A})=Var((X^TX)^{-1}X^TY)=(X^TX)^{-1}X^TVar(Y)X(X^TX)^{-1}=V_\epsilon^2(X^TX)^{-1}
である。これと(1')から、
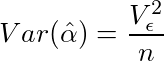
Var(\hat{\alpha})=\frac{V_\epsilon^2}{n}
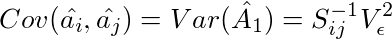
Cov(\hat{a_i},\hat{a_j})=Var(\hat{A_1})=S_{ij}^{-1}V_\epsilon^2
がわかる。

問題のVar(a0)については、
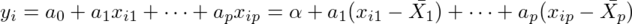
y_i=a_0+a_1x_{i1}+\cdots+a_px_{ip}=\alpha+a_1(x_{i1}-\bar{X_1})+\cdots+a_p(x_{ip}-\bar{X_p})
の関係より
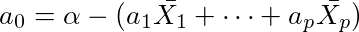
a_0=\alpha-(a_1\bar{X_1}+\cdots+a_p\bar{X_p})
であるから、

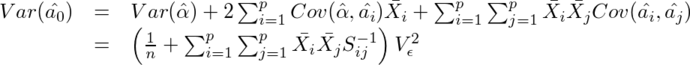
となる。