統計学復習メモ8: 回帰直線と主成分分析

高校生の時に、必要も無いのに関数電卓を買った覚えがある。物理の先生に、理系ならずっと使うから早目に買っといて損は無いとか言われたからだと思うが、結局大学で物理実験をやるまでは遊びでしか使わなかった。それでも、元々電卓が好きだった私は、毎日毎日、関数電卓のプラスチックのボタンをカチャカチャと押して遊んでいた。
その電卓には、「一次回帰直線」の係数を求める機能があった。学校では習わなかったが、説明書にy=a+bxのaとbを求める機能と書いてあったので、意味は分かった。来る日も来る日も自室に逃げ込んで電卓と戯れてる内に、「一次回帰直線」がとても身近なものになった。

そんなに一次回帰直線に慣れ親しんだから、主成分分析には敏感に反応した。というのも、主成分分析は繰り返し回帰直線を求めることに似ていると思うからである。

一次回帰直線とは、パラメトリックな２変量の関係を直線で近似するものなので、２次元のデータを１次元で近似することに相当する。２変量をx,yとすると、標本(x1,y1)〜(xn,yn)の関係を直線y=a+bx（a,bは定数）で近似するので、その直線との誤差を無視して(x,y)=(0,a)+(1,b)tと置くと、２変量の標本(xi,yi)が１変量tiで表せるのである。
主成分分析の第一主成分だけを使うことを考えると、多変量の関係を１次元で近似することになるから、k次元の標本(x1i,x2i,...,xki)を(C1,C2,...,Ck)+(p1,p2,...,pk)tiに近似すると、k個の変量を持つ標本(x1i,x2i,...,xki)が１変量tiだけで表せる。(C1,C2,...,Ck)は定数ベクトルで、(p1,p2,...,pk)が第一主成分の単位ベクトルである。第二主成分の単位ベクトルを(q1,q2,...,qk)としてこれも使うとすると、(x1i,x2i,...,xki)≒(C1,C2,...,Ck)+(p1,p2,...,pk)si+(q1,q2,...,qk)tiという感じに、k変量の標本を２変量で近似することになる。

一次回帰直線の最小２乗法による求め方をおさらいする。標本(xi,yi)と直線y=a+bxとの誤差はyi-a-bxiであるが、この誤差の２乗和を最小にするようにa,bを決めたい。誤差の２乗和をEとすると、E=Σ(yi-a-bxi)2で、このEはaの２次関数であり、bの２次関数でもあるから、Eをaで偏微分したものが0になるaと、Eをbで偏微分したものが0になるbを求めれば良い。
\frac{\partial E}{\partial a}=0, \frac{\partial E}{\partial b}=0
これを解くと、
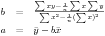
b\frac{\sum xy - \frac{1}{n}\sum x\sum y}{\sum x^2-\frac{1}{n}(\sum x)^2},a=\bar{y} - b\bar{x}
が得られる。bの分子はxとyの共分散、分母はxの分散なので、xの分散をVar(X)、xとyの共分散をCov(X,Y)と表すと、b=Cov(X,Y)/Var(X)とも書ける。実はシンプルである。

念のため、試しにやってみて確認する。例によってMaximaを使う。サンプルデータをdata1とし、

data1: read_nested_list("data1");
datam: read_matrix("data1");
load(descriptive);
b: cov(datam)[1][2] / var(datam)[1];
a: mean(datam)[2] - b * mean(datam)[1];
とすると、b=-.8338664607943058、a=5.848350705139143と求まる。そこで
plot2d([[discrete, data1], a+b*x],[x,0,2],[style,[points],[lines]]);
とすると、次のグラフが作られる。

主成分分析についても、詳細を省いて、とりあえずサンプルデータ(data2)を使って図示してみる。
下のように、標本が原点を中心に楕円盤状に散らばっているとする。（どれかの画像をクリックするとgifアニメが開きます）



少しずつ回転させてみたが、わかりづらいので、大体の分布の形を枠線で表示する。


第一主成分の単位ベクトルは最も誤差の和を小さくする直線の方向、すなわち楕円の長径方向の長さ１のベクトルになる。次の図の青線が第一主成分（をスカラー倍したもの）である。


標本から第一主成分を抜く（第一主成分を0にする）と、下の図のようになる。（回転方向は変更）


つまり、第一主成分と垂直な平面への射影である。元が楕円盤状だったのでこれも楕円状であり、この楕円を最も近似した直線、すなわち長径方向が第二主成分の向きになる。（下図緑線）


３次元なので、第二主成分も抜くと、直線状になる。その直線は第一主成分、第二主成分と直交し、その直線上に第三主成分がある。

空間が何次元でも同様である。最も誤差が小さくなる近似直線の方向の大きさ１のベクトルが第一主成分の単位ベクトルであり、その方向のベクトル成分を抜いた（超平面に射影した）ものの近似直線の方向の大きさ１のベクトルが第二主成分の単位ベクトルであり、その方向のベクトル成分も抜いて...を繰り返すと、全ての主成分が出てくる。

そんな反復計算をせずに主成分分析する方法は、次回まとめる。

上で書いた以外の、今回使ったMaximaへの入力をメモする。
共通ヘッダ
load(descriptive);
load(distrib);
２次元サンプルデータ作成用（パターン１：行列形式）
data0: map(lambda([x],[x,random_normal(0,1)*sqrt(1-x^2)]/3),
makelist(random(2.0)-1,x,1,100)),numer$
rotate(x) := matrix([cos(x),-sin(x)],[sin(x),cos(x)])$ /* 回転行列 */
kill(f);f[i,j]:=data0[i][j]$ /* なぜかf[]は上書きされない */
tmp: genmatrix(f,100,2)$ /* ２次元配列→行列への変換 */
datam: tmp.rotate(-%pi/4),numer$
write_data(datam,"data1");
２次元サンプルデータ作成用（パターン２：配列形式）
data0: map(lambda([x],[x,random_normal(0,1)*sqrt(1-x^2)/5]),
makelist(random(2.0)-1,x,1,100)),numer$
th: -%pi/4$
data1: map(lambda([z],float([
cos(th)*z[1] - sin(th)*z[2] + 1,
sin(th)*z[1] + cos(th)*z[2] + 5
])), data0)$ /* 行列形式と違って、このままplot2dできる */
plot2d([discrete,data1],[style,points]);
write_data(data1, "data1");
一次回帰分析の組み込みモジュール使用（MaximaのHelpを参照）
load("stats");
z:simple_linear_regression(data1);
３次元サンプルデータ作成用
data0:map(lambda([x],[x, random_normal(0,0.5)*sqrt(1-x^2)/2,
random_normal(0,1)*sqrt(1-x^2)*sqrt(3/4)/10
]), makelist(random(2.0)-1,x,1,100)),numer$
write_data(data0,"data0"); /* 回転前 */
data1: read_matrix("/tmp/data0")$
trZ(x):= matrix([cos(x),sin(x),0],[-sin(x),cos(x),0],[0,0,1]);
trX(x):=matrix([1,0,0],[0,cos(x),sin(x)],[0,-sin(x),cos(x)]);
data2: data1.trZ(%pi/4).trX(%pi/4),numer$
write_data(data2,"data2"); /* 回転後 */
data3: data2 - data2.matrix([0.714],[0.488],[0.5]).matrix([0.714,0.488,0.5])$
write_data(data3, "data3"); /* 第一主成分と直交する平面への射影 */
/* Maxima 5.17のplot3dがdiscrete plotに対応していないため、グラフはgnuplotのコマンドで表示する */
楕円盤ワイヤーフレーム作成用
frame0: [cos(x)*cos(y), sin(x)*cos(y)/2, sin(y)/10];
frame1: transpose(trX(-%pi/4).trZ(-%pi/4).frame0);
plot3d(frame1[1], [x,0,2*%pi], [y,0,2*%pi]);
frame2: frame1 - frame1.matrix([0.714],[0.488],[0.5]).matrix([0.714,0.488,0.5]);
plot3d(frame2[1], [x,0,2*%pi], [y,0,2*%pi])$

３次元グラフ作成用(gnuplot)
共通ヘッダ

set term x11 font "Helvetica,16"
set xyplane at 0
set ticslevel -0.5
set zeroaxis
set zzeroaxis
set ztics axis
set border 15

set xlabel "x"
set ylabel "y"
set zlabel "z"
set xrange [-1:1]
set yrange [-1:1]
set zrange [-1:1]

set parametric
サンプルデータのみのグラフ
splot "data2" title "sample"
サンプルデータとワイヤーフレーム
splot "data2" title "sample", "frame" title "frame" with lines
サンプルデータと第一主成分
splot "data2" title "sample", 0.714*u,0.488*u,0.5*u title "component1"
超平面への射影と第一主成分と第二主成分
splot "data2" title "sample", 0.714*u,0.488*u,0.5*u title "component1", "data3" title "projection", -0.7*u,0.55*u,0.457*u title "component2"
GIFアニメは、3Dのview pointを少しずつ動かすgnuplotの入力をPerlで作って、できた画像をImageMagickで合成して作った。（Perlスクリプトの例はこちら）
ImageMagickのコマンドの例
convert -delay 10 ??.png anim.gif


今回は統計の勉強というよりはMaximaとgnuplotの勉強になってしまった。
燃え尽きた。


大学に入ってすぐ「最小２乗法」による直線への近似を学んだが、それが関数電卓が言う「一次回帰直線」を求めることだとは、１年くらい気付かなかった。自宅で実験レポートを書いてる時にそれが同一であることを知った時の驚きは、人生最大のアハ体験だった。なぜか大学の先生が誰も「一次回帰」という言葉を使わなかったから、わからなかったのである。先生方に対してその言葉を口にしたら100%通じたのだが、なぜ誰も「一次回帰」と言わなかったのかが、未だに不思議で仕方が無い。

上の一次回帰直線求め方で、標本と回帰直線との誤差をY軸方向の距離としているが、その距離は直線に対して垂直に取らないとまずいのではないか、と疑問に思うことがあるが、２次元だと直線に対して垂直方向の距離は必ずY軸方向の距離の定数倍（正確にはcos(Y軸と回帰直線がなす角度)倍、もちろん回帰直線がY軸に一致する(Var(X)=0)場合を除いて）になるので、距離の合計を最小にする目的では問題ない。（３次元以上だと別である。例えば、XYZ空間の回帰直線がXY平面上にあるとして、Z=0の標本でも回帰直線との距離は0とは限らないことが容易に想像できる）