平日、子供を毎朝7:30までに起こす為に、「めざましテレビ」の7:30〜7:59の間に2回ある「めざましじゃんけん」をさせている。勝ったら20pt、引き分けなら10pt、負けたら5ptで、週内100ptでクリアである。
5日×2回/日=10回の点数の期待値は10*(20+10+5)/3 > 116なので、まあまあの確率でクリアできそうであるが、今週は負けまくって、月〜金で無事に10回やり切ったのに、10回やった中では初めてクリアできなかった。
そこで、10回でクリアできる確率はどれくらいだろうかと思って考え始めたら、場合の数を数え上げる以外の方法が思い付かなかった。
クリアできない方が少ないので、クリアできない方を数え上げる。
4勝以上だと全敗でもクリアなので、0
3勝だと7敗のみなので、10C3 = 120
2勝だと3分以下なので、10C2 * (8C3 + 8C2 + 8C1 + 8C0) = 4185
1勝だと6分以下=2敗以下以外なので、10C1 * (29 - 9C2 - 9C1 - 9C0) = 4660
0勝だと9分以下=0敗以外なので、210 - 1 = 1023
全ての場合の数は310 = 59049なので、クリアできない確率は (120 + 4185 + 4660 + 1023) / 59049 = 9988 / 59049 = 0.169 、クリアできる確率はその逆で0.831である。
こんな計算方法しか無かったっけ?
なお、10回分の点数の確率分布は、モンテカルロ法でやってみたら、こんな感じだった。
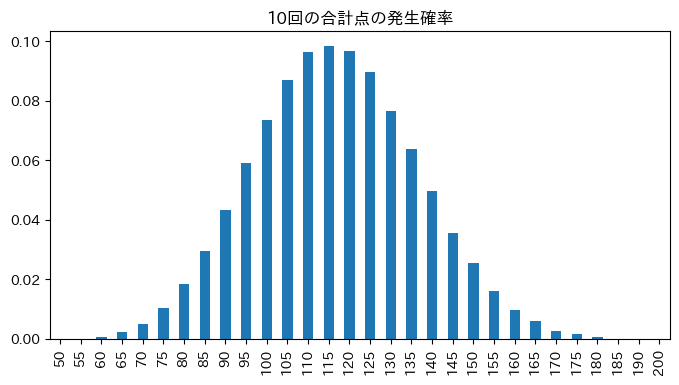
コメント