「岩波データサイエンス Vol.1 [特集] ベイズ推論とMCMCのフリーソフト」という本を借りたので読んでみると、PyMCというライブラリを使えばPythonでもできると書かれていたので、サンプルコードがBUGSやRで書かれている例題を含めて全てPyMCでやってみることにした。
BUGSやRのコードを読み解きながら、p.39〜p.46辺りの、時系列データに状態空間モデルのトレンドモデルや、観測モデルに対数正規分布を用いたモデルを当てはめてパラメーター推定する例題まで順調に進められたが、p.47〜p.48の「観測値が二項分布のモデル」でPyMCのトラブルに遭遇した。その回避方法がわかったので、ここに記す。
まず成功例として、p.45辺りの、観測モデルに対数正規分布を用いた例を紹介する。
なお、今回はなるべくこの本のサンプルコードと比較できるように、サンプルコードに近い形で書くことを目指している為、PyMCを上手く使う書き方にはしていない。例えば、PyMCではモデル作成時にループを使うことが推奨されていないようである。そもそも筆者はPyMCを使い始めたばかりで、ではどう書くのが良いのかがわからない。
import matplotlib.pyplot as plt
# 年輪データ
# https://github.com/iwanami-datascience/vol1/blob/master/ito/nenrin.data より借用
nenrin_data = [
4.71, 7.7 , 7.97, 8.35, 5.7 , 7.33, 3.1 , 4.98, 3.75, 3.35, 1.84, 3.28, 2.77, 2.72, 2.54,
3.23, 2.45, 1.9 , 2.56, 2.12, 1.78, 3.18, 2.64, 1.86, 1.69, 0.81, 1.02, 1.4 , 1.31, 1.57]
index = range(1960, 1990)
plt.plot(index, nenrin_data, color='k')
plt.ylabel('Tree-ring width')
plt.show()
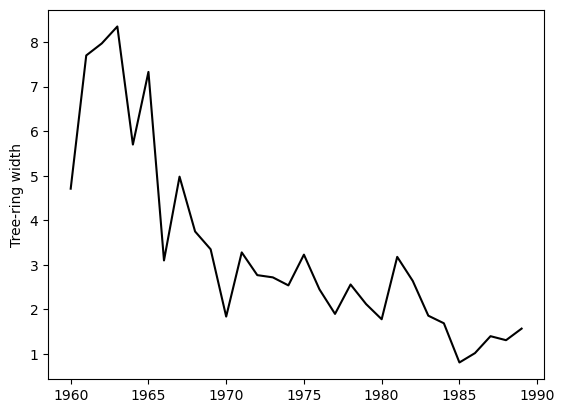
こういう、京都市内で採取された杉の木の年輪幅の推移のデータがあり、これに次のような状態空間モデルを当てはめる。
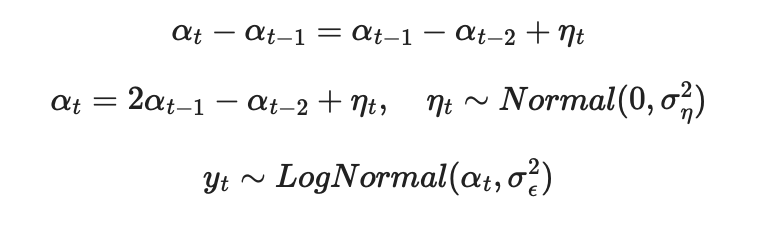
αtが年輪幅で、1行目はαtのシステムモデルとしてトレンドモデルを仮定するもの、2行目は1行目を変形したもの、3行目は観測モデルである。 このαtを次のコードで推定する。
●コード
import pymc as pm
import pandas as pd
N = nenrin_data.shape[0]
with pm.Model() as model:
# 事前分布
alpha = [pm.Uniform('alpha1', 0, 10), pm.Uniform('alpha2', 0, 10)]
sigma = [pm.Uniform('sigma1', 0, 10), pm.Uniform('sigma2', 0, 10)] # σ_ε, σ_η
# システムモデル
for i in range(2, N):
alpha.append(pm.Normal(f'alpha{i+1}', mu=2 * alpha[i-1] - alpha[i-2], sigma=sigma[1]))
# 観測モデル
y = []
for i in range(N):
y.append(pm.LogNormal(f'y{i+1}', mu=alpha[i], sigma=sigma[0], observed=nenrin_data['width'].iloc[i]))
with model:
trace = pm.sample(10000, progressbar=False)
# 結果の可視化
# alphaはyの対数に対応しているのでexp(alpha)に変換している
import numpy as np
plt.plot(index, nenrin_data, color='k', label='observed')
# 事後分布の平均
alpha_mean = [trace['posterior'][f'alpha{i+1}'].mean() for i in range(N)]
alpha_mean_exp = np.exp(alpha_mean)
plt.plot(index, alpha_mean_exp, color='b', linewidth=2, label='posterior')
# 95%ベイズ信用区間
alpha_025 = [np.percentile(trace['posterior'][f'alpha{i+1}'], 2.5) for i in range(N)]
alpha_975 = [np.percentile(trace['posterior'][f'alpha{i+1}'], 97.5) for i in range(N)]
alpha_025_exp = np.exp(alpha_025)
alpha_975_exp = np.exp(alpha_975)
plt.fill_between(index, alpha_025_exp, alpha_975_exp, color='cyan', alpha=0.15, label='95% credible interval')
plt.ylabel('Tree-ring width')
plt.legend()
plt.show()
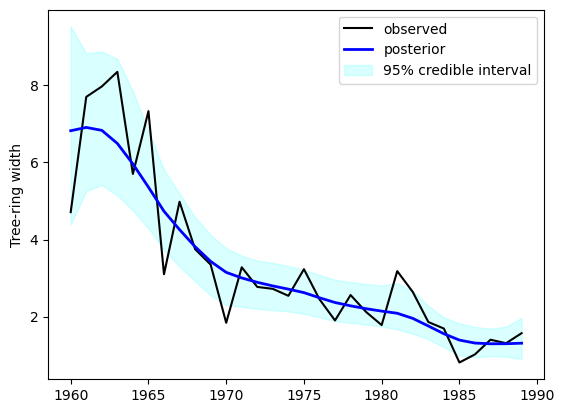
この結果は本に記載されている図とほぼ同じである。
次に、1つ目の問題が発生した、p.47〜p.48の「観測値が二項分布のモデル」の例である。
ある林にいる鳥の数をカウントするとする。 鳥の個体を発見できる確率をp、1回の観測につき5回(i=1〜5)繰り返しカウントする、それを50回(t=1〜50)観測するとする。 実際には観測できない真の個体数Ntは期待値λtのポアソン分布に従うとする。
t回目の観測におけるi回目のカウントでの発見個体数をNtiobs とすると、観測モデルは次のようになる。
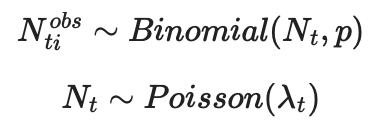
λtは対数スケールで、分散σ2の正規分布に従ってランダムウォークするとすると、システムモデルは次のようになる。
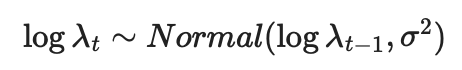
import numpy as np
# 模擬データ作成
np.random.seed(5)
Nt = 50
Nr = 5
p = 0.6
sigma = 0.1
# log λ_t
log_lambda = [np.log(30)]
for i in range(1, Nt):
log_lambda.append(log_lambda[i-1] + np.random.normal(0, sigma))
# 真の個体数
N_true = [np.random.poisson(np.exp(log_lambda[i])) for i in range(Nt)]
# 発見個体数
Nobs = np.array([np.random.binomial(N_true[t], p, Nr) for t in range(50)])
# 可視化
import matplotlib.pyplot as plt
plt.plot(range(1, Nt+1), N_true, color='k', linewidth=0.5, label='true')
plt.scatter([[t+1]*5 for t in range(50)], Nobs, marker='.', alpha=0.5, label='observed')
plt.xlabel('time')
plt.title('Bird count')
plt.legend(loc='upper center')
plt.show()
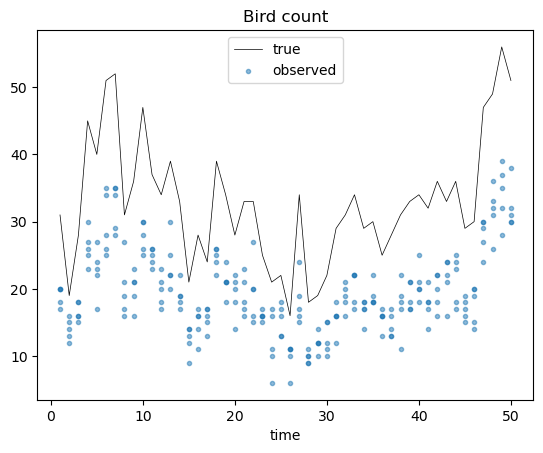
このデータから真の個体数を推定するとする。
上の成功例と同じ要領で、次のようなコードを実行すると、CompileErrorが発生した。
# 発見個体数からのパラメーター推定
import pymc as pm
# CompileError対策
# import pytensor
# pytensor.config.gcc__cxxflags += ' -fbracket-depth=384'
Nt = 50 # Nt >= 32だとCompileErrorになる
Nr = 5
p = None
log_lambda = None
sigma = None
N = None
with pm.Model() as model:
# 事前分布
p = pm.Uniform('p', 0, 1)
log_lambda = [pm.Normal('loglambda[1]', 0, 100)] # sigma=100は書籍だと1e-4だが、それだと結果がかなりずれる
sigma = pm.Uniform('sigma', 0, 100)
# システムモデル
for t in range(1, Nt):
log_lambda.append(pm.Normal(f'loglambda[{t+1}]', mu=log_lambda[t-1], sigma=sigma))
# 観測モデル
l = [pm.Deterministic(f'lambda[{t+1}]', log_lambda[t].exp()) for t in range(Nt)]
N = [pm.Poisson(f'N[{t+1}]', mu=l[t]) for t in range(Nt)]
Y = [pm.Binomial(f'Nobs[{t+1}]', n=N[t], p=p, observed=Nobs[t]) for t in range(Nt)]
# 初期値を与えないとSamplingErrorになる
initvals = {f'N[{t+1}]': 100 for t in range(Nt)}
with model:
trace = pm.sample(10000, initvals=initvals)
CompileError: Compilation failed (return status=1):
/Users/ynomura/.pytensor/compiledir_macOS-14.5-arm64-arm-64bit-arm-3.10.14-64/tmp7dc45x_s/mod.cpp:26982:32: fatal error: bracket nesting level exceeded maximum of 256
if (!PyErr_Occurred()) {
^
/Users/ynomura/.pytensor/compiledir_macOS-14.5-arm64-arm-64bit-arm-3.10.14-64/tmp7dc45x_s/mod.cpp:26982:32: note: use -fbracket-depth=N to increase maximum nesting level
HINT: Use a linker other than the C linker to print the inputs' shapes and strides.
HINT: Re-running with most PyTensor optimizations disabled could provide a back-trace showing when this node was created. This can be done by setting the PyTensor flag 'optimizer=fast_compile'. If that does not work, PyTensor optimizations can be disabled with 'optimizer=None'.
HINT: Use the PyTensor flag `exception_verbosity=high` for a debug print-out and storage map footprint of this Apply node.
筆者の環境は、macOS 14.5 + python 3.10.14 + PyMC 5.15.0 + PyTensor 2.20.0 だった。PyMCはpipでインストールしたものである。
コードのコメントにも書いたが、色々試した結果、 Nt = 31 なら発生しないことがわかったので、Pythonのコードが間違っている訳ではなさそうだった。
Webで検索すると、このCompileErrorが発生したと書かれているページがいくつか見つかったが、具体的な解決方法が見つけられなかった。
PyMCのサイトにAnacondaやMiniforgeを使ってインストールすることを推奨すると書かれているので、Miniforgeを使ったインストールも試したが、結果は同じだった。その環境は python 3.12.3 + PyMC 5.15.1 + PyTensor 2.22.1だった。
上のエラーメッセージから、Cコンパイラの{}のネストが最大ネスト数の256を超えたというエラーが出ており、コンパイラの引数に-fbracket-depth=Nを加えると最大ネスト数が変えられると書いてある。色々調べた結果、次の2行(上のコードではコメントアウトしている)を加えると、このCompileErrorを回避できた。
import pytensor
pytensor.config.gcc__cxxflags += ' -fbracket-depth=384'
import matplotlib.pyplot as plt
import numpy as np
x = range(1, Nt+1)
plt.plot(x, N_true[:Nt], color='k', linewidth=0.5, label='true')
plt.scatter([[t+1]*5 for t in range(50)], Nobs, marker='.', alpha=0.5, label='observed')
lambda_mean = [trace['posterior'][f'lambda[{t+1}]'].mean() for t in range(Nt)]
plt.plot(x, lambda_mean, color='b', linewidth=2, label='posterior lambda')
# 95%ベイズ信用区間
lambda_025 = [np.percentile(trace['posterior'][f'lambda[{t+1}]'], 2.5) for t in range(Nt)]
lambda_975 = [np.percentile(trace['posterior'][f'lambda[{t+1}]'], 97.5) for t in range(Nt)]
plt.fill_between(x, lambda_025, lambda_975, color='cyan', alpha=0.15, label='95% credible interval')
plt.xlabel('time')
plt.title('Bird count')
plt.legend()
plt.show()
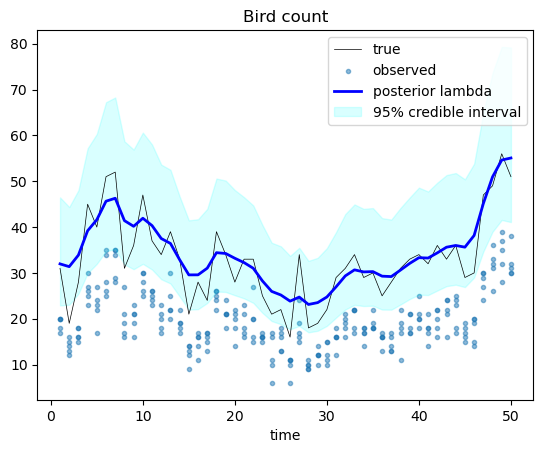
他の対策として、システムモデルがランダムウォークの場合はpymc.GaussianRandomWalkという丁度良いものがあった。今回は書籍のサンプルコードとの対応を重視したのでこれで良しとしなかったが、一応やってみたので、そのコードも貼り付ける。
●コード
# 発見個体数からのパラメーター推定
import pymc as pm
Nt = 50
Nr = 5
p = None
log_lambda = None
sigma = None
N = None
with pm.Model() as model:
# 事前分布
p = pm.Uniform('p', 0, 1)
sigma = pm.Uniform('sigma', 0, 100)
# システムモデル
log_lambda = pm.GaussianRandomWalk('loglambda', mu=0, sigma=sigma, steps=Nt-1)
# 観測モデル
l = pm.Deterministic('lambda', log_lambda.exp())
N = pm.Poisson('N', mu=l)
Y = pm.Binomial(f'Nobs', n=N[[i // Nr for i in range(Nt*Nr)]], p=p, observed=Nobs.reshape(-1))
# 初期値を与えないとSamplingErrorになる
initvals = {'N': [100] * Nt}
with model:
trace = pm.sample(10000, initvals=initvals)
# 結果の可視化
import matplotlib.pyplot as plt
import arviz as az
x = range(1, Nt+1)
plt.plot(x, N_true, color='k', linewidth=0.5, label='true')
plt.scatter([[t+1]*5 for t in range(50)], Nobs, marker='.', alpha=0.5, label='observed')
lambda_mean = pm.summary(trace, var_names='lambda')['mean']
plt.plot(x, lambda_mean, color='b', linewidth=2, label='posterior lambda')
# 95%ベイズ信用区間
hdi = az.hdi(trace, hdi_prob=0.95, var_names='lambda')
plt.fill_between(x, hdi['lambda'][:,0], hdi['lambda'][:,1], color='cyan', alpha=0.15, label='95% credible interval')
plt.xlabel('time')
plt.title('Bird count')
plt.legend()
plt.show()
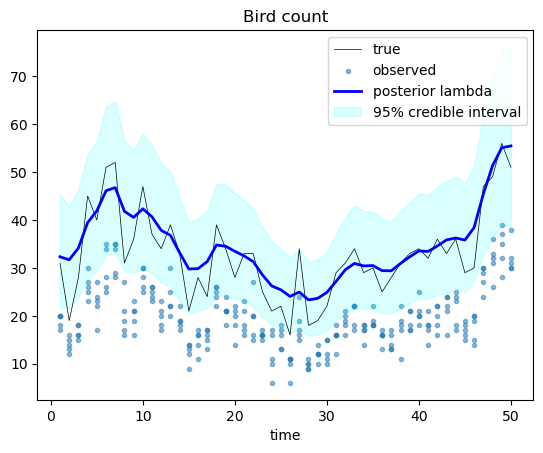
上の結果とほぼ同じだが、ベイズ信用区間が少し下にずれてかつ狭くなったので、僅かに改善したと思う。
この本は良書だと思った。わかりやすかったし、ベイズ推論の理解が進んだと思った。興味深い例題も多く、やってみて納得した。PyMCのトラブルで、本を読む時間と本のサンプルコードを読みながらコードを書く時間の3倍くらいの時間を奪われてしまったが、概ね(上のコードのコメントの"1e-4"以外)この本の問題ではなかった。
コメント