カルマンフィルターの例題として、何らかの物理的な物体があり、内部状態として位置xと速度vがあり、それぞれがノイズの影響を受け、観測できるのはxに観測誤差を加えたzのみとし、位置xを一定の目標値に制御したいとする。
次のコードのPhysicalModelを制御対象とする。xを取得するメソッドがあるが、制御する際に観測できるのはzだけであり、xの本当の値は観測できないとする。
import numpy as np
import matplotlib.pyplot as plt
class PhysicalModel(object):
x_std = 1.0 # 位置xのノイズの標準偏差
v_std = 0.5 # 速度vのノイズの標準偏差
z_std = 2.0 # xの観測誤差の標準偏差
def __init__(self, timesteps, init_x, init_v, random_seed=1):
np.random.seed(random_seed)
self.x = np.zeros(timesteps) # 位置x(便宜上過去の値を保存)
self.v = np.zeros(timesteps) # 速度v
self.a = np.zeros(timesteps) # 加速度a
self.z = np.zeros(timesteps) # xの観測値z
# t=0
self.t = 0 # 時刻
self.x[0] = init_x
self.v[0] = init_v
self.z[0] = self.x[0]
# 時刻tを1つ進める
def step(self):
self.t += 1
self.x[t] = self.x[t-1] + 0.99 * self.v[t-1] + 1/2 * self.a[t-1] + self.x_std * np.random.randn(1)[0]
self.v[t] = 0.98 * self.v[t-1] + self.a[t-1] + self.v_std * np.random.randn(1)[0]
self.z[t] = self.x[t] + self.z_std * np.random.randn(1)[0]
return self.z[t] # 1つ進めた時刻の観測値を返す
# 時刻tの加速度を入力する
def set_accel(self, a):
self.a[t] = min(10, max(-10, a)) # 実際には -10 <= a <= 10 に制限されるとする
# t=offset以降のxの目標値からの平均二乗誤差
def MSE(self, mean, offset=0):
return sum((self.x[offset:] - x_target) ** 2) / self.x[offset:].shape[0]
# グラフ表示用
def get_x_history(self):
return self.x[:t+1]
def get_v_history(self):
return self.v[:t+1]
def get_a_history(self):
return self.a[:t+1]
def get_z_history(self):
return self.z[:t+1]
まず、カルマンフィルターを用いず、観測値zを使って制御してみる。
xの初期値は20、目標値は5とする。
制御入力は、ノイズやvの減衰を無視すると
xt+1 = xt + vt + (1/2) at
なので
at = 2 (xt+1 - (xt + vt))
であり、次の時刻(t+1)で目標値に到達させるなら
at = 2 (x_target - (xt + vt))
だが、観測値zから推測したx,vはノイズを含むので、その影響を小さくする為、入力するaは上の式の半分とする。(実際、上の式の2を色々変えてみても1.0前後くらいが良さそうだった。時刻(t+2)で目標値に到達させるべく、
xt+2 = xt + 2vt + 2 atから
at = (1/2) (x_target - (xt + 2vt))
とするのも有効そうだったが、今回は単純な例で試す。)
timesteps = 50
init_x = 20
x_target = 5
model = PhysicalModel(timesteps, init_x=init_x, init_v=0)
estimated_v = [0] # vの推定値、グラフ表示用に保存する
z_prev = init_x # t=0の観測値
a = 0 # t=0の加速度
for t in range(1, timesteps):
z = model.step()
# x,vの推定
# z = z_prev + v_prev + a/2
# v = v_prev + a
# -> v = z - z_prev - a/2 + a
x = z
v = z - z_prev + a/2
estimated_v.append(v)
# 制御入力
a = 1.0 * (x_target - (x + v))
model.set_accel(a)
z_prev = z
print("MSE =", model.MSE(x_target, offset=10))
fig = plt.figure(figsize=(10,4))
ax1 = fig.gca()
ax2 = ax1.twinx()
ax1.plot(model.get_z_history(), label='observed')
ax1.plot(model.get_x_history(), color='r', linewidth=2, label='true_x')
ax2.plot(model.get_v_history(), 'y', alpha=0.5, label='true_v')
ax2.plot(estimated_v, 'y', linestyle='--', label='estimated_v')
ax1.grid(axis='y')
ax1.set_ylim((-2, 22))
ax1.set_xlabel('time')
ax1.set_ylabel('x')
ax2.set_ylabel('v')
ax1.legend(loc='upper right', bbox_to_anchor=(1, 0.7))
ax2.legend(loc='upper right')
ax1.set_title("Controlling x to 5")
plt.show()
# 別の制御方式との比較用
true_x_1 = model.get_x_history()

MSE = 5.654622082289254
赤線が制御対象のxである。一応、xが5辺りに制御されている。
次に、カルマンフィルターを用いてx,vを推定しながら制御してみる。
制御対象を状態空間モデルで表すと、このようになる。
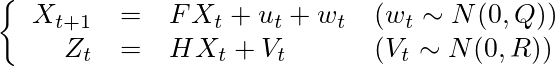
上の式が状態方程式、下の式が観測方程式と呼ばれるものである。
ここでのXは位置xと速度vを含む状態ベクトル、
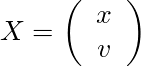
であり、時刻tからt+1の間にシステム行列Fによる状態遷移と、制御入力uと、平均0、分散Qの多変量正規分布に従うノイズwが加わるとする。
Zは状態Xの観測値で、Xが観測行列Hにより変換され、平均0、分散Rの多変量正規分布に従うノイズVが加わるとする。(このVは小文字のvで表記されることが多いが、今回の例では速度のvと紛らわしいので、ここでは大文字で記す)
制御入力uは加速度aにより、vの減衰を無視すると、ノイズを除いた部分は
xt+1 = xt + vt + (1/2) at
vt+1 = vt + at
となるので、
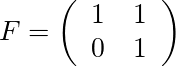
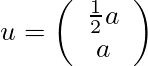
となる。
状態はxしか観測できないので、観測行列Hは[1 0]となる。
Q,Rは最小二乗法で推定する方法があるらしいが、今回は経験的にこれくらいだと知っているものとして、それぞれ[[1, 0], [0, 0.1]]と[5]とする。
次のコードはpykalmanを用いた例である。
●コード
# pykalmanのカルマンフィルターを使う例
from pykalman import KalmanFilter
model = PhysicalModel(timesteps, init_x=init_x, init_v=0)
kf = KalmanFilter(
transition_matrices=[[1, 1], [0, 1]],
observation_matrices=[1, 0],
transition_covariance=[[1, 0], [0, 0.1]],
observation_covariance=[5],
# initial_state_mean=[init_x, 0], # 今回の使い方では関係無かった
# initial_state_covariance=[[0, 0], [0, 0]] # 何にしても変わらない
)
filtered_state = np.zeros((timesteps, 2)) # x,vの推定値、グラフ表示用に保存する
filtered_state[0] = [init_x, 0]
filtered_state_cov = np.zeros((timesteps, 2, 2)) # x,vの推定値の分散
a = 0 # t=0の加速度
for t in range(1, timesteps):
z = model.step()
# x,vの推定
filtered_state[t], filtered_state_cov[t] = kf.filter_update(
filtered_state[t-1],
filtered_state_cov[t-1],
z,
transition_offset=np.array([1/2 * a, a])
)
x, v = filtered_state[t]
# 制御入力
a = 1.0 * (x_target - (x + v))
model.set_accel(a)
print("MSE =", model.MSE(x_target, offset=10))
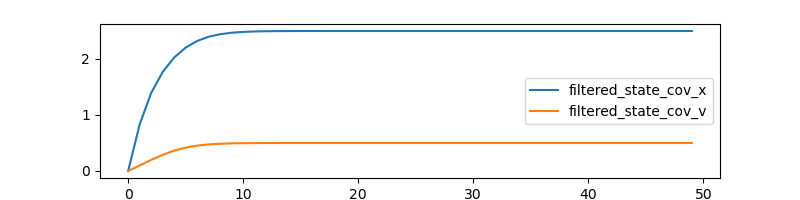
# 安定確認
plt.figure(figsize=(8,2))
plt.plot(filtered_state_cov[:,0,0], label='filtered_state_cov_x')
plt.plot(filtered_state_cov[:,1,1], label='filtered_state_cov_v')
plt.legend()
plt.show()
fig = plt.figure(figsize=(10,4))
ax1 = fig.gca()
ax2 = ax1.twinx()
ax1.plot(model.get_z_history(), label='observed')
ax1.plot(filtered_state[:,0], linestyle='--', label='filtered_x')
ax1.plot(true_x_1, color='r', alpha=0.3, label='true_x(prev)')
ax1.plot(model.get_x_history(), color='r', linewidth=2, label='true_x')
ax2.plot(model.get_v_history(), 'y', alpha=0.5, label='true_v')
ax2.plot(filtered_state[:,1], 'y', linestyle='--', label='filtered_v')
ax1.grid(axis='y')
ax1.set_ylim((-2, 22))
ax1.set_xlabel('time')
ax1.set_ylabel('x')
ax2.set_ylabel('v')
ax1.legend(loc='upper right', bbox_to_anchor=(1, 0.7))
ax2.legend(loc='upper right')
ax1.set_title("Controlling x to 5")
plt.show()
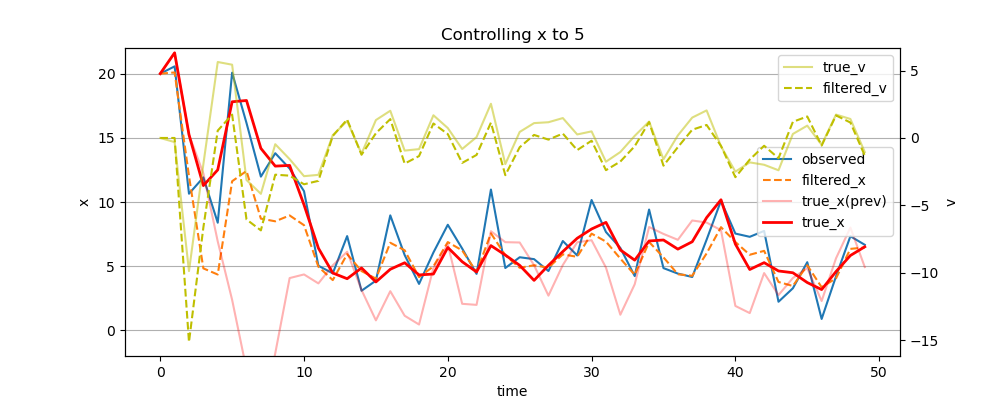
MSE = 3.238811619518345
濃い赤線が制御対象のx、青線が観測値、オレンジの点線がxの推測値である。全体的には推定値が観測値より本当のxに近いように見える。薄い赤線が上のカルマンフィルターを使わない例のxであり、何となく、今回の方がよりx=5の近くに制御されているように見える。また、黄色の実線が本当のv、黄色の点線が推測したvであり、観測していないvがそれにりに正しく推測され、本当のvも0付近で安定している。
出力のt≧10のMSEで見ても、誤差が小さくなっている。
次のコードはfilterpyを使って同じ結果を得たものである。詳細は省略する。
●コード
# filterpyのカルマンフィルターを使う例
from filterpy.kalman import KalmanFilter
model = PhysicalModel(timesteps, init_x=init_x, init_v=0)
kf = KalmanFilter(dim_x=2, dim_z=1)
kf.F = np.array([[1, 1], [0, 1]])
kf.B = np.eye(2)
kf.H = np.array([[1, 0]])
kf.Q = np.array([[1, 0], [0, 0.1]])
kf.R = 5
kf.x = np.array([[init_x, 0]]).T
kf.P = np.zeros((2, 2))
filtered_state = np.zeros((timesteps, 2))
filtered_state[0] = [init_x, 0]
filtered_state_cov = np.zeros((timesteps, 2, 2))
a = 0
for t in range(1, timesteps):
z = model.step()
# x,vの推定
kf.predict(u=np.array([[1/2 * a, a]]).T)
kf.update([z])
filtered_state[t] = kf.x[:, 0]
filtered_state_cov[t] = kf.P
x, v = filtered_state[t]
# 制御入力
a = 1.0 * (x_target - (x + v))
model.set_accel(a)
print("MSE =", model.MSE(x_target, offset=10))
MSE = 3.2388116195183434
ドキュメントが充実しているし、不具合の原因解析の為にソースコードを読む羽目になってもソースコードがわかりやすかったので、苦労は少なかったが、パラメーターの設定は初期値に乗算する方法もあるなど違和感のある記述があったり、class KalmanFilterのdim_uを指定してもBの初期値がNoneだったりしたので、完成度が低いのかなと思った。あまり使われていないのだろうか。著者の書籍の為に作成したライブラリなのだろうか?
最後に、次のコードは、statsmodels.tsaのMLEModelを使って同じ結果を得たものである。
詳細は省略するというより、理解できなかったので説明できない。
# statsmodelsのMLEModelを使う例
import statsmodels.api as sm
model = PhysicalModel(timesteps, init_x=init_x, init_v=0)
filtered_state = np.zeros((timesteps, 2))
filtered_state[0] = [init_x, 0]
filtered_state_cov = np.zeros((timesteps, 2, 2))
a = 0
# 毎回t=0から推定する為に制御入力を残す
state_intercept_history = np.zeros((2, timesteps))
for t in range(1, timesteps):
z = model.step()
# x,vの推定
observed_state = model.get_z_history()
state_intercept_history[:, t-1] = [1/2 * a, a]
# 毎回MLEModelのインスタンスを作成するしかなさそう
# 状態の分散の初期値が与えられなかったので毎回t=0から推定する
kf = sm.tsa.statespace.MLEModel(observed_state[0:t+1], k_states=2)
kf._state_names = ['x', 'v']
kf['transition'] = np.array([[1, 1], [0, 1]])
kf['state_intercept'] = state_intercept_history[:, :t+1]
kf['selection'] = np.eye(2) # X(t+1) = F X(t) + u(t) + w(t)のw(t)の前に掛けるもの
kf['state_cov'] = np.array([[1, 0], [0, 0.1]])
kf['design'] = np.array([[1, 0]]) # 観測行列
kf['obs_cov'] = np.array([[5]])
kf.initialize_known(filtered_state[0], filtered_state_cov[0])
filter_result = kf.filter([])
filtered_state[t] = filter_result.filtered_state[:, t]
filtered_state_cov[t] = filter_result.filtered_state_cov[:, :, t]
x, v = filtered_state[t]
# 制御入力
a = 1.0 * (x_target - (x + v))
model.set_accel(a)
print("MSE =", model.MSE(x_target, offset=10))
MSE = 3.238811619518343
こちらは、同じ結果を得るのに非常に苦労した。とにかく、ドキュメントがひどい。書かれていないことが多い。しかも、用語が特殊でわかりにくい。ソースコードが読めたものではない。
Web上にはstatsmodels.tsaのUnobservedComponentsを使った例が多いと感じたが、UnobservedComponentsでは状態の初期値が設定できない。まずここで躓いた。
初期値を与えるにはMLEModelを使うとの情報を得て、MLEModelのドキュメントを読むと、最初に目に飛び込んでくるのが"endog", "exog"という名称で、まずこれで「??」となる。"endogeneous"=内生の、"exogeneous"=外生の、らしいが、何でこんな用語を使うのだろう。
それに、設定すべきパラメーター及び設定方法が書かれていない。下位層はKalmanFilterクラスというようなことが書かれており、KalmanFilterのドキュメントを読むとAttributesの説明があるが、結局これを設定する手段が書かれていないし、サンプルコードも無い。
KalmanFilterのドキュメントにはextend()など今回の用途に適してそうなメソッドがあったので、これを使うのが正しいかと思ったが、KalmanFilterクラスがstatsmodels.api以下に無く、直接使うのが適切なのかどうかがわからなかった。
MLEModelには"endog"を差し替える手段が無さそうなので、clone()で"endog"だけが異なるインスタンスを作ろうと思ったら、"NotImplementedError"が出た。
仕方なく、時刻tとt-1だけの"endog"のMLEModelを毎回作成するようにしようとしたら、ある程度近い結果が得られるようになったが、どうしても計算が合わなかった。細かく調べた結果、initialize_known()のinitial_state_cov(状態の分散の初期値)として2x2の行列を与えると、内部でその要素がバラバラになってしまい(行列の2行目が異なる時刻の1行目として扱われる)、状態の分散が正しく計算されないようだった。
今回の例ではたまたま状態の分散の初期値を0にしていたので、時刻0からtまでの"endog"のMLEModelを毎回作成することによって、何とか他のライブラリと同じ結果を得ることができた。
取り組みの途中から、もしかして直接KalmanFilterクラスを使うのが正しいんじゃないかと思っていたが、MLEModelで1回やり切るのに疲れ切って、調査を断念した。
そもそもstatsmodels.tsa.statespaceは時系列データ分析が主目的のようで、あまり制御への応用目的では考えられていない感じがする。
現在も更新されていってるようなのでこれから完成度が上がるのだろうと思うし、時系列データ分析では既にseasonal decompositionやSTL分解などで何度もお世話になってるので、次はカルマンフィルターを時系列データ分析に応用する時にお世話になることにする。
コメント