統計学復習メモ7: t検定で独立性の検定

前のエントリーではカイ２乗検定を用いてノンパラメトリック（定性的）な独立性の検定を試したが、次はパラメトリック（定量的）な場合をやってみる。独立かどうかを確かめたい２つの属性が定量的な値を持つパラメーター、Ｃ言語で言うとenum型やchar型でなくint型やfloat型の変数である場合に、その２変数間に相関があるかどうかを検定するものである。

なお、統計学では独立、相関という言葉はノンパラメトリックかパラメトリックかで使い分けるのが通常なのかも知れないが、ここでは区別せず、独立である／ないと相関がない／あるは同じ意味で使う。

まず、実際に例題でやってみる。

ある事業分野において、過去に優秀なプログラマーが書いた、読んで理解し易いしその後の仕様変更にも強いと評判の良い、模範的なＣ言語のソースコード一式があったとする。ソースファイル中のコード量（文の数や式の数、a=0;やb=foo(a);は１つ、while(式)はwhileと式とで２つ、for(式１;式２;式３)は４つ等）とコメントの量（/*～*/内の文字数）の関係が以下であった時、コード量とコメント量との間に相関がある無いかを検定したいとする。

ファイル名	コード量	コメント量
gentoo.h	88	234
emperor.h	98	413
macaroni.h	485	687
rockhopper.h	285	438
fairy.h	184	194
magellan.h	487	174
humboldt.h	818	344
king.h	69	139
adelie.h	306	244
cape.h	219	222

ファイル名	コード量	コメント量
gentoo.c	519	1876
emperor.c	515	2995
macaroni.c	78	517
rockhopper.c	313	1839
fairy.c	392	2142
magellan.c	369	1783
humboldt.c	345	2762
king.c	73	489
adelie.c	729	2202
cape.c	445	2309

統計学で相関と言えば、まず思い付くのは相関係数である。とりあえず、ヘッダファイルとソースファイルに分けて、コード量とコメント量の相関係数を求めてみる。
よく使われる相関係数は、共分散÷それぞれの分散の幾何平均、というもので、式で書くと、２つのパラメーターを持つ標本が(x₁,y₁)～(x_n,y_n)の時、
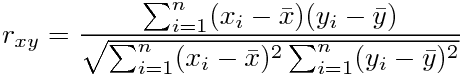
$r_{xy}=¥frac {¥sum_{i=1}^{n}(x_i-¥bar{x})(y_i-¥bar{y})} { ¥sqrt{ ¥sum_{i=1}^{n}(x_i-¥bar{x})^2 ¥sum_{i=1}^{n}(y_i-¥bar{y})^2 }}$
と表されるものである。（ピアソンの積率相関係数という名前が付いているらしい。）
例によってMaximaに計算させると、ヘッダファイルについてはr≒0.327、ソースファイルについてはr≒0.746であった。

さて、この値をどう考えれば良いのだろう。２つのパラメーターに十分に直線関係があるかどうかの基準として使われるものの１つに、相関係数が0.99以上（強い正の相関）または-0.99以下（強い負の相関）か、というのがある。検量線などの回帰直線の適切さの基準として使われることがあるようだが、そのように基準を決める自由がある場合ならそれでいいだろうが、一般的には（一般論としては）0.99という数字に根拠が無い。では相関係数がどういう値なら何なのだろうか。

そこで、検定統計量
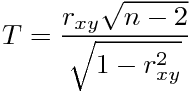
$T=¥frac{r_{xy}¥sqrt{n-2}}{¥sqrt{1-r_{xy}^2}}$
が自由度n-2のｔ分布に従うという定理を使うのが、統計学の尊い教えである。

仮説を「相関がない」とし、有意水準を0.05（信頼度を95%）とすると、自由度n-2のｔ分布で右側（ｔが大きい方）の棄却域はt≧2.3くらいである。それに対し、ヘッダファイルについてはT≒0.978、ソースファイルについてはT≒3.17なので、ヘッダファイルについては仮説が棄却されず、コード量とコメント量の間に相関があるとは言えない、ソースファイルについては仮説が棄却され、コード量とコメント量の間に（正の）相関がある、ということになる。

結局、この方法では、相関係数はいくらぐらいだと相関があると言えるのだろうか。
まず、相関係数rと検定統計量Tの関係を見ておく。n=5,10,15,20の時のTのグラフは、次のようになる。

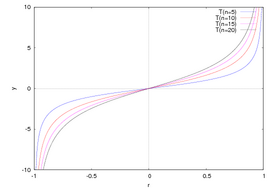
単調増加、点対称である。
Tがｔ分布に従うと、rの分布は次のグラフのようになる。

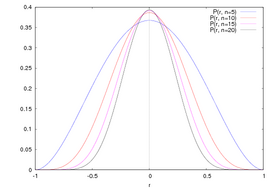
当たり前だが、rが-1（負の相関）や+1（正の相関）に近いのは稀だということになっていることがわかる。
Tがｔ分布の両側5%の境目になるrの絶対値は、以下の値である。

n	r
5	0.878
10	0.632
15	0.514
20	0.444

相関係数の絶対値がこれらより大きければ、相関があるということになる。
思ったより緩い基準である。

今回用いたMaximaの入出力を控えておく。

(%i1) load(descriptive);    /* おまじない */
(%i2) load(distrib);
(%i3) m: matrix([519,1876],[515,2995],[78,517],[313,1839],[392,2142],[369,1783],[345,2762],[73,489],[729,2202],[445,2309]);
(%i4) cor(m),numer;    /* 相関係数行列（ソースファイル） */
                   [ .9999999999999999  .7462318886705528 ]
(%o4)              [                                      ]
                   [ .7462318886705529  .9999999999999999 ]
(%i5) r: cor(m)[1][2],numer;    /* 相関係数（ソースファイル） */
(%o5)                          .7462318886705528
(%i6) n: 10;
(%i7) r*sqrt(n-2)/sqrt(1-r^2),numer;    /* 検定統計量（ソースファイル） */
(%o7)                          3.170657389340475
(%i8) m: matrix([88,234],[98,413],[485,687],[285,438],[184,194],[487,174],[818,344],[69,139],[306,244],[219,222]);
(%i9) cor(m),numer;
(%i10) r: cor(m)[1][2],numer;    /* 相関係数（ヘッダファイル） */
(%o10)                         .3268873235524222
(%i11) r*sqrt(n-2)/sqrt(1-r^2),numer;    /* 検定統計量（ヘッダファイル） */
(%o11)                         .9783227786739287
(%i12) quantile_student_t(0.975,n-2);    /* 自由度n-2のｔ分布の右側2.5%のｔ */
(%o12)                         2.30600413520253
(%i13) makelist(1/sqrt(1+(n-2)/(quantile_student_t(0.975,n-2)^2)),n,[5,10,15,20]), numer;    /* n=[5,10,15,20]の時の、検定統計量が右側2.5%になるr */
(%o13) [.8783394481597959, .6318968647195646, .5139774683398788, .4437633993377761]

グラフ作成用。

plot2d([r*sqrt(5-2)/sqrt(1-r^2),r*sqrt(10-2)/sqrt(1-r^2),r*sqrt(15-2)/sqrt(1-r^2),r*sqrt(20-2)/sqrt(1-r^2)],
[r,-1,1],[y,-10,10],[nticks,100],
[legend, "T(n=5)","T(n=10)","T(n=15)","T(n=20)"],
[plot_format, gnuplot],[gnuplot_term, ps],
[gnuplot_out_file, "corr_t.eps"])$

plot2d([
pdf_student_t(r*sqrt(5-2)/sqrt(1-r^2), 5-2),
pdf_student_t(r*sqrt(10-2)/sqrt(1-r^2), 10-2),
pdf_student_t(r*sqrt(15-2)/sqrt(1-r^2), 15-2),
pdf_student_t(r*sqrt(20-2)/sqrt(1-r^2), 20-2)
], [r,-1,1],
[legend, "P(r, n=5)","P(r, n=10)","P(r, n=15)","P(r, n=20)"],
[plot_format, gnuplot],
[nticks,100],[gnuplot_term, ps],
[gnuplot_out_file, "corr_pr.eps"])$

模範的なＣのソースファイルはコード量とコメント量の間に相関がある、という検定結果は、あくまでここでの例題に限っての話である。筆者はそんな話を聞いたことが無い。
また、上記の文の数や式の数をコード量とする尺度は、筆者の創作であり、私の会社で使われていたりする訳ではない。

参考になったサイトへのリンク：
http://www.geisya.or.jp/~mwm48961/koukou/index_m.htm（下の方に統計関連のページあり、わかりやすい）

Weblog on mebius.tokaichiba.jp

統計学復習メモ7: t検定で独立性の検定

コメント

Cah