統計学復習メモ6: χ2検定で独立性の検定

以前のメモではカイ２乗検定の例としてばらつきの検定（適合度の検定）をやってみたが、もう１つのカイ２乗検定の使われ方として、独立性の検定がある。これもやってみる。

プログラマー35歳定年説というのがある。あるプロジェクトにおいて、
35歳未満で、受けたバグ指摘件数が20件未満のプログラマーが45人、
35歳未満で、受けたバグ指摘件数が20件以上のプログラマーが15人、
35歳以上で、受けたバグ指摘件数が20件未満のプログラマーが25人、
35歳以上で、受けたバグ指摘件数が20件以上のプログラマーが15人、
だったとする。表にすると、

O(a,b)B<20B≧20
age<354515
age≧352515
（Bはバグ票数）である。暗雲が立ちこめてきたが、信頼度を95%として、35歳以上であることとバグ票数20件以上であることに相関はあるだろうか。

まず、age≧35とB≧20が独立の場合の理論値を計算する。age<35が60人、age≧35が40人、B<20が70人、B≧20が30人なので、これだけから考えると、B<20の70人は60:40でage<35とage≧35に分かれるので、それぞれ42人、28人である。同様に、B≧20の30人は18人、12人に分かれる。

E(a,b)B<20B≧20
age<354218
age≧352812
帰無仮説を、相関がない（独立である）と取ると、観測値が理論値から大きくばらついていれば棄却されるので、ピアソンのカイ２乗検定が使える。χ2分布に従う、ピアソンの検定統計量
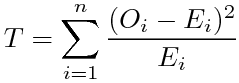
T=￥sum_{i=1}^n￥frac{(O_i-E_i)^2}{E_i}
を計算すると、T=(45-42)2/42 + (25-28)2/28 + (15-18)2/18 + (15-12)2/12≒1.79となる。このTは、4つの理論値を固定すると、4つの観測値のどれか1つが決まると定まるので、自由度は1である。自由度が1のχ2分布の左側が95%になるχ2の値は3.84なので、今回のTはばらついていない方（χ2が小さい＝理論値の通りに近い方）の95%に入っており、仮説は棄却されず、相関があるとは言えないことになる。

これは、B≧20かどうかで分けたのが明暗を分けた可能性があり、もしB≧25で分けると

O(a,b)B<25B≧25
age<35555
age≧353010
だったりした場合はT=5.23でOuchとなるので、あまりいい例ではないかも知れないが、そこまでは敢えて考えないことにする。


同じ考え方で、2つの属性で2x2に分類したデータから2つの属性の独立性を検定する方法を定式化してみる。1か2かを取る2つの属性をa,bとし、母数がnの、それぞれの属性の組み合わせに属する標本数の観測値を

O(a,b)b=1b=2
a=1x11x12
a=2x21x22
(x11+x12+x21+x22=n)とする。a,bを独立とした場合の期待値は、b=1について(a=1):(a=2)=(x11+x12):(x21+x22)、a=1について(b=1):(b=2)=(x11+x21):(x12+x22)...となるので、
nE(a,b)b=1b=2
a=1(x11+x12)(x11+x21)(x11+x12)(x12+x22)
a=2(x11+x21)(x21+x22)(x12+x22)(x21+x22)
の定数倍である。これらを全て足すと(x11+x12+x21+x22)2=n2なので、これらが期待値のn倍であり、1/nすれば期待値になることがわかる。
E(a,b)b=1b=2
a=1(x11+x12)(x11+x21)/n(x11+x12)(x12+x22)/n
a=2(x11+x21)(x21+x22)/n(x12+x22)(x21+x22)/n
これを、
O(a,b)b=1b=2sum
a=1x11x12a1
a=2x21x22a2
sumb1b2n
という風に行和、列和を取って整理すると、
E(a,b)b=1b=2
a=1a1b1/na1b2/n
a=2a2b1/na2b2/n
となる。検定統計量Tは、各セルの(O-E)2/Eを合計したものなので、
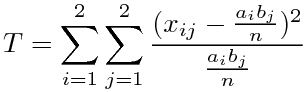
T=¥sum_{i=1}^{2}¥sum_{j=1}^{2}¥frac{(x_{ij}-¥frac{a_ib_j}{n})^2}{¥frac{a_ib_j}{n}}
と書ける。これを自由度1のχ2分布のχ2の値として見れば良いわけである。

aがp個の値、bがq個の値を取る時も同じことが言えるので、
T=¥sum_{i=1}^{p}¥sum_{j=1}^{q}¥frac{(x_{ij}-¥frac{a_ib_j}{n})^2}{¥frac{a_ib_j}{n}}
（aiはa=iの標本の和、bjはb=jの標本の和）
となる。自由度は、aについては(p-1)、bについては(q-1)なので、全体としては(p-1)(q-1)である。

以上を踏まえて、もう１つ例題をやってみる。原理はわかったので、手計算チックな計算は卒業して、次はMaximaに組み込みのカイ２乗検定関数を使おう、と思って関数を探すと、手元のMaximaには入ってなかった。ExcelにはCHI2TEST()という名前でデフォルトで入ってるのだが、Maximaにはデフォルトでは入っていないらしい。上記の計算だけなら大して複雑じゃないので、自分で関数を作ってみる。 

chi2test(x_,row_,col_):=block([i,j,n,a,b,chi2],
    a:map(lambda([i],sum(x_[i][j],j,1,col_)),create_list(i,i,1,row_)),
    b:map(lambda([j],sum(x_[i][j],i,1,row_)),create_list(j,j,1,col_)),
    n:sum(a[i],i,1,row_),
    chi2:sum(sum((x_[i][j]-a[i]*b[j]/n)^2/(a[i]*b[j]/n),j,1,col_),i,1,row_),
    print("chi^2=",chi2),
    print("95% confidence at",quantile_chi2(0.95,(row_-1)*(col_-1))),
    print("90% confidence at",quantile_chi2(0.90,(row_-1)*(col_-1))),
    chi2
)$
試しに
chi2test([[45,25],[15,15]],2,2),numer;
（numerは結果が分数になるのを避けるため）とやってみると、 
chi^2= 1.785714285714286
95% confidence at 3.841458820694166
90% confidence at 2.705543454095465
と出力される。信頼度90%でも、２つの属性が独立である仮説は棄却されないことになる。

次の例は、バグの原因を設計ミス要因かコーディングミス要因かに分けて、さらにそれをプログラマーの年齢層で分けて数えてみたという架空のデータである。

O(a,b)設計ミスコーディングミス
30歳以上35歳未満176195
35歳以上40歳未満85139
40歳以上45歳未満90106
年齢層とバグの原因との間に相関はあるだろうか。

chi2test([[176,195],[85,139],[90,106]],3,2),numer;
これを実行すると、次の出力が得られる。 
chi^2= 5.35085981290286
95% confidence at 5.991464547107982
90% confidence at 4.605170185988094
従って、信頼度を95%とすると、年齢層とバグの原因が独立であるという仮説は棄却されない。
信頼度を95%とすると、である。

なお、上記のchi2test()を正しく動かすには、先に以下の２行を実行しておく必要がある。 
load(descriptive);
load(distrib);