統計学の検定というのは、「帰無仮説」と「対立仮説」を設定して、「帰無仮説」を「棄却」できれば「対立仮説」が「有意」であるとする、というものである。
...というように言葉で書かれるとそんなに難しくなさそうなのだが、ここまでで既に「帰無仮説」だの「有意」だの独特の用語が出てくる上、帰無仮説が棄却できない時は「対立仮説が有意であるとは言えない」だの「差が無いという仮説は棄却されない」だの「差があるとは言えない」だの回りくどい表現が出てきて、混乱する。
棄却して「無」に「帰」するための仮説だから「帰無仮説」と言うんだよ、なんて説明は大して理解の助けにならない。むしろ、それで何か解った気にさせて思考を停止させる、本質の理解を邪魔する雑音にすら思える。
なぜ「差が無いとは言えない」ではないのか。そういう疑問を持ってもう一度理解しようとすると、「第1種の過誤」や「第2種の過誤」や「有意水準」や「危険率」や「検出力」が出てきて、阻止されてしまう。命題の逆が偽(矛盾する)なら命題が真となるような単純な代物ではないのである。
筆者は大学で「検定」を習って15年以上、統計学を復習して1年以上、まだ混乱している。そのため、自己流に整理して、悪あがきしてみる。
仮説として、ある統計量が、下の図の緑色の線で示されるような確率分布に従うと仮定されているとし、標本から得られた統計量がtであるとする。横軸がt、縦軸が発生確率である。

上記の仮説が正しいとすると、t=0.7(青い点の辺り)やt=1.5(紫色の点の辺り)はまだそれなりに発生確率が高いが、t=2.2(赤い点の辺り)は発生確率が低い。従って、t=2.2となるような標本が得られたら、それはかなり稀な事が起こったという事になる。その時、そうではなくて仮説が誤っているのだと考えるのが統計学における検定の考え方である。
そのために、どれくらい稀だと仮説が誤っているとする(仮説を棄却する)かを決める。その確率が有意水準である。何故だかわからないが、0.05や0.01がよく使われるようである。ここでは有意水準を0.05(5%)とする。
次に、統計量がどの範囲だと仮説を棄却するか(棄却域)を、その範囲の発生確率が有意水準に等しくなるように決める。例えば、上図の緑色で塗った部分は、0から遠い、発生確率が全体の5%の範囲である。すなわち、標本のtがこの範囲(大体t<2とt>2)に入れば、仮説を棄却する、という設定である。
注意すべきは、仮説を棄却できなかったからといって仮説が正しいとは言えないことである。仮説が正しいとすると稀にしか起こらない事が起こったかどうか、を調べているだけなので、わかるのは、仮説が誤っているか、何とも言えないか、のどちらかである。調べている仮説を帰無仮説、その反対の仮説を対立仮説として言い換えると、わかるのは、帰無仮説が誤っていて対立仮説が有意であるか、帰無仮説が誤っているとは言えず対立仮説については何とも言えないか、のどちらかである。
上記の設定では、もし標本から得られたtが青や紫の位置の値なら、仮説が棄却できず(検定失敗)、いわゆる玉虫色の決着となるが、もしtが赤い位置の値なら、仮説が間違っているだろうと言える。
以上で検定の計算は可能だが、設定した検定方法が妥当かどうか、また検定結果の意味を考えるためには、他に考える事がある。
帰無仮説にて統計量の確率分布を仮定するということは、標本の統計量にもばらつきがあることを仮定している。もし標本の統計量にばらつきが無いとするなら、棄却域に入るかどうかという以前に、ばらつきがあるとする帰無仮説が誤りになってしまう。
例えばもし、標本の統計量が帰無仮説の通りでないのに、平均的には棄却域に入らない場合は、次のような感じになる。
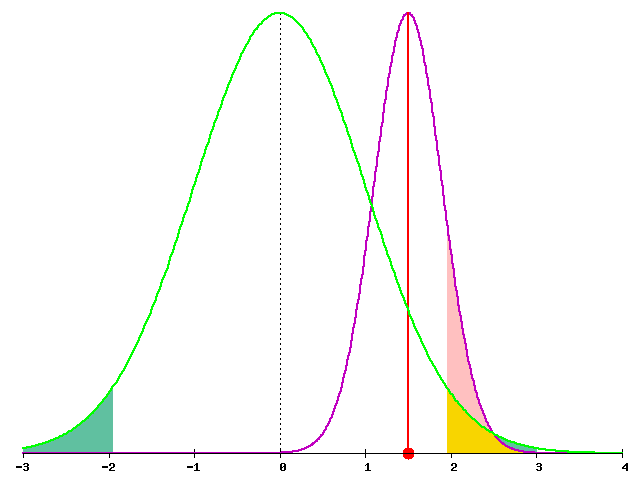
赤い点が統計量の平均、紫色の線が分布である(見やすさのため、縦に縮めている)。ピンクで塗られている部分が、帰無仮説(緑線)の棄却域に入る部分である。
もし帰無仮説が正しい場合は、紫の線は緑の線に一致し、ピンクの領域は有意水準と同じ5%となる。そのため、帰無仮説が正しくても、5%の確率で帰無仮説が棄却されてしまう(第一種の誤り)。帰無仮説は棄却するために設定する(誤りだろうと思うものを帰無仮説に採る)ものだが、棄却できたと喜んでも、誤って棄却した可能性が残るのである。有意水準は、この第一種の誤りを犯す確率という意味で、危険率とも呼ばれる。
上の図では、緑の線と紫の線はずれており、帰無仮説は誤りである。しかし、ピンクの領域、すなわち帰無仮説が棄却される確率は12.5%しかない。「検出力」が12.5%しか無い、と言う。
次の図は、統計量の平均が棄却域に入るくらいにずれている例である。
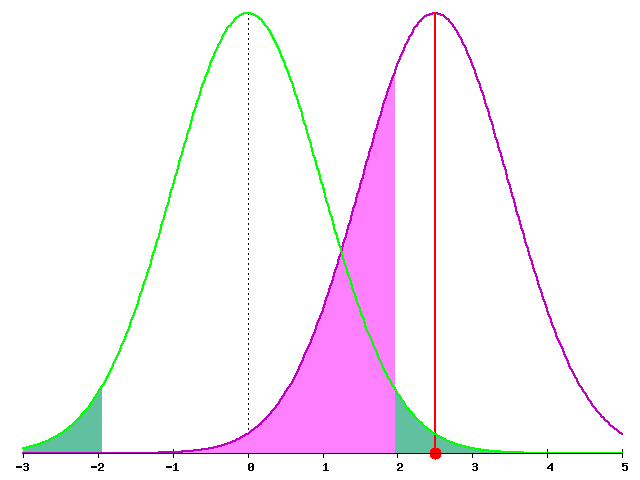
ピンクで塗っていないが、ここまでずれると検出力は70%に達する。しかし、逆に言うと、ここまで帰無仮説が誤っていても、30%の確率で棄却されないのである(第二種の誤り)。有意水準を下げて第一種の誤りを犯す確率(緑の領域)を小さくすると、第二種の誤りを犯す確率(藤色の領域)が大きくなる、という関係があることがわかる。
次に、帰無仮説と棄却域の取り方について考える。
通常、帰無仮説は「差が無い」方に取られる。これは、統計量が0から遠い方が「差がある」ことが多いというか、0から遠い方が「差がある」ように統計量を定める方が便利であることが多いからである。例えば標準正規分布やt分布やカイ2乗分布に従う統計量は0から遠いと平均と差がある。
そのため、もし帰無仮説を「差がある」方に取ると、統計量の棄却域が0に近い方になり、範囲が狭くなる。標準正規分布やt分布のような山形の分布だと、
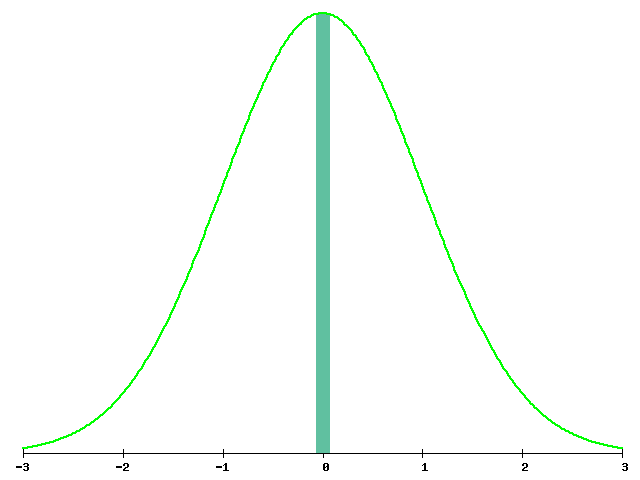
このように棄却域が狭くなり、統計量が繊細で、計算上不便である。
それよりも、実際の検定統計量は和や積を使って計算されるため、「差がある」は単純ではなく、棄却するのは難しいのである。例えば、和で効いてくる平均値の場合、実際には標本に帰無仮説と全然違う大きなばらつきがあっても、相殺されて帰無仮説の平均値に近くなってしまうことがあり得るし、積で効いてくる場合は標本のどれか1つの確率が(帰無仮説の前提から外れて)0に近いために結果として統計量が0に近くなってしまうことがあり得る。「差がある」を棄却するには色々な可能性を考えないといけないが、統計量が0から遠ければそれだけで「差が無い」を棄却できるので、やりやすいのである。
そのため、上の例のように統計量が標準正規分布やt分布などの0中心の左右対称の確率分布に従うと仮定する場合は、棄却域を0から遠い左右両端に定めることが多い(両側検定という)。
カイ2乗分布に従う統計量のように、正の値しか取らない場合は、0から遠い方の(+∞までの)1つの領域を棄却域とする(片側検定という)場合が多いが、それでも、どこかに山がある場合は0に近い方の裾と0から遠い方の裾の両側に棄却域を設ける場合もあるようである。
次の図は、カイ2乗検定(片側検定)の棄却域の例である。

緑の線が、統計量が自由度2のカイ2乗分布に従うという帰無仮説であり、緑で塗られた領域が有意水準(αと書かれることが多い)5%の棄却域である。赤い点のように、標本から得られた統計量がここに入れば、緑の線を棄却する。
実際には自由度4のカイ2乗分布に従う場合は、帰無仮説と標本は次のような関係になる。

藤色の部分が第二種の誤りを犯す範囲(βと書かれることが多い)で、確率は約0.8であり、ピンク色の部分の大きさが検出力であり、(1-β)≒0.2である。
短くまとめたつもりが、結局長くなってしまった。
やっぱりややこしい。
検定とは棄却域を設定することである、という。なるほどと思った。
●今回作ったMaximaのソース
グラフ作成部分が長いので別ファイルにする。
h_test.wxm(wxMaximaの"Evaluate All Cells"で実行可能、Maximaでも実行可能)
(%i3) quantile_normal(0.975,0,1);
(%o3) 1.959963984540054
(%i11) 1-cdf_normal(1.96,t1,s1),numer; /*1-β(グラフ2)*/
(%o11) .1250719356371504
(%i15) cdf_normal(1.96,t1,s1),numer; /*1-β(グラフ3)*/
(%o15) 0.294598516215698
(%i16) 1-%; /*β(グラフ3)*/
(%o16) .7054014837843019
(%i25) 1-cdf_chi2(quantile_chi2(0.95,chi0),chi1);
(%o25) .1997866136776991
コメント