統計学復習メモ14: ポアソン分布のパラメーターの最尤推定量

筆者はある会社のソフトウェア関係の部署に在籍しているが、一般にはソフトウェア開発とは呼ばれない補助的な仕事をしている。調達担当や購買担当という呼び方が最尤推定量であろう。そんな筆者にもお呼びがかかるのが、不再現バグの再現試験である。
バグ発生の報告があったが、開発担当者が解析するために再現させようとしても、再現しない。発生した証拠はある。となると、総出で再現試験である。

そのバグを発生させるべく、100回も200回も同じ操作をしていると、いつまでやらないといけないのだろうと不安になってくる。1万回やっても出ない可能性もあるのである。仮に発生確率が1/1000だったとしても、1000回やったら必ず1回は出る訳ではない。確率が低い事象の発生回数は「小数の法則」ポアソン分布に従う。発生回数（発生確率×試行回数）の平均がλの場合、発生回数がkになる確率は、
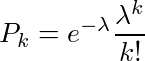
P_k=e^{-¥lambda}¥frac{¥lambda^k}{k!}
である。
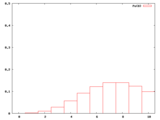
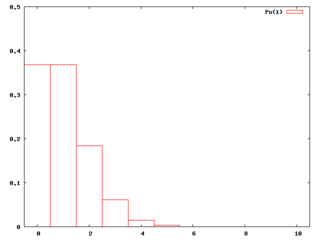λ=1のポアソン分布の確率密度
従って、1000回やって平均1回しか起こらないものが1000回やって1回も起こらない確率は1/e≒36.8%もある。1回起こる確率が同じく1/e、従って2回以上起こる確率が(1-2/e)≒26.4%であるが、1回も起こらない確率が36.8%もあるのだ。既に何百回も起こらないでなぜ＋思考になれようか。

自分が毎回その1/eに入るのを不思議に思いながらも、誰かが再現させて解放される。最初に再現させる人は1人しかいないのだから、自分がその1人になる確率は低いので、左脳で考えると当たり前である。複数人でのべ2000回やって1回起こったとすると、結果として発生率は1/2000である。
さて、本題である。この時、本当の発生率も1/2000と推定できるのだろうか？実は本当の発生率が1/5000の時が2000回に1回発生する確率が一番高かったりしないのだろうか？
これはまあ、P(k=1)=λe-λが

こんな形をしてるので、P(k=1)をλで偏微分して=0とすると、(1-λ)e-λ=0でλ=1ということになり、1回発生する確率が最も大きいのはλ=np=1すなわちp=1/2000と力技で求められる。

では、もし、ある人は200回で発生させ、ある人は500回で発生させ、ある人は1000回で発生させたら、その発生率は全て足し合わせて3/1700と推定するものなのだろうか？
問題を整理すると、ポアソン分布のパラメーターλの推定量λ^は何なのだろうか？


今回は、最尤推定法を使うことにする。最尤推定法とは、あるパラメーターθを持つ確率分布を仮定して、結果として標本X1...Xnが得られた時、n個の標本を取ると前記の標本X1...Xnが得られる確率が最も高いθを求める方法である。X1...Xnが得られる確率をP(X1)...P(Xn)とし、X1...Xnが独立（１つ前の標本によって発生率が変わったりしない）とすると、それらが同時に起こる確率はL(θ)=P(X1)×P(X2)×...×P(Xn)である。これが最大になるθ=θ^を求めるのである。さらにL(θ)が単峰（山頂＝極大点が１つしかない）なら、そのθは
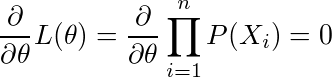
¥frac{¥partial}{¥partial¥theta}L(¥theta) = ¥frac{¥partial}{¥partial¥theta}¥prod_{i=1}^{n}P(X_i) = 0
の解である。積の形だと何なので、対数を取って
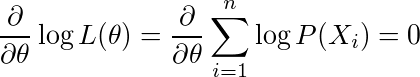
¥frac{¥partial}{¥partial¥theta}¥log L(¥theta) = ¥frac{¥partial}{¥partial¥theta}¥sum_{i=1}^{n}¥log P(X_i)=0
の解でもあるのであるのである。

ポアソン分布のλについては、
¥frac{¥partial}{¥partial¥lambda}¥log P_k = ¥frac{¥partial}{¥partial¥lambda}¥log e^{-¥lambda¥frac{¥lambda^k}{k!}} = ¥frac{¥partial}{¥partial¥lambda}(-¥lambda+k¥log¥lambda-¥log(k!)) = -1 + ¥frac{k}{¥lambda}
なので、L(λ)が最大になるλを求めると、
¥frac{¥partial}{¥partial¥lambda}¥log L(¥lambda)=¥sum_{i=1}^{n}(-1+¥frac{X_i}{¥lambda})=0
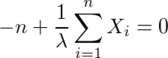
-n+¥frac{1}{¥lambda}¥sum_{i=1}^{n}X_i=0
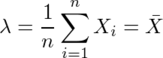
¥lambda=¥frac{1}{n}¥sum_{i=1}^{n}X_i=¥bar{X}
となるので、標本平均が最尤推定量である。

元の問題に戻って、X1=1/200、X2=1/500、X3=1/1000と置くと、平均λ=(X1+X2+X3)/3=8/3000=1/375となる。

...と言いたい所だが、これだと200回に1回出した人が1000回に5回出すということを仮定していることになるので、見方によってはやっぱり3/1700のような気もする。
そもそも、発生した時点で試行を止めたとしたら、そこまでの回数を使うのでは、発生率が高目に出てしまう。考え直した方が良さそうだ。


本文で使わなかったが、λ=2〜10の整数についてもポアソン分布の確率密度のグラフを作ったので、ついでに並べておく。








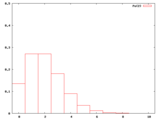
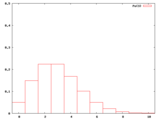
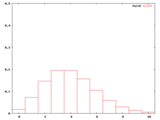
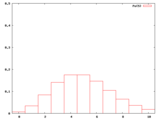
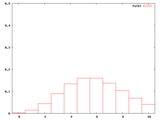
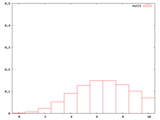
以下、今回使ったMaximaとgnuplotのソースを記録する。
・k=1のポアソン分布のλと確率のグラフ作成用(Maxima)
set_plot_option([gnuplot_pipes_term,png]);
plot2d(x*%e^(-x),[x,0,10],[gnuplot_term,png],[gnuplot_out_file,"poisson2.png"],[gnuplot_preamble,"set grid; set xtics border 0,1,10;"]);
・λ=1〜10のポアソン分布(Po(λ))の確率データ作成用(Maxima)
p(L):= map(lambda([k],[k, %e^(-L)*L^k/k!]), [0,1,2,3,4,5,6,7,8,9,10]);
write_data(float(p(1)), "po1");
write_data(float(p(2)), "po2");
write_data(float(p(3)), "po3");
write_data(float(p(4)), "po4");
write_data(float(p(5)), "po5");
write_data(float(p(6)), "po6");
write_data(float(p(7)), "po7");
write_data(float(p(8)), "po8");
write_data(float(p(9)), "po9");
write_data(float(p(10)), "po10");
・gnuplotでの棒グラフ作成用（Maximaで棒グラフを作るのは面倒なので）
set term png
set xrange [-0.5:10.5]
set yrange [0:0.5]
set output "Po1.png"
plot 'po1' with boxes title "Po(1)"
set output "Po2.png"
plot 'po2' with boxes title "Po(2)"
set output "Po3.png"
plot 'po3' with boxes title "Po(3)"
set output "Po4.png"
plot 'po4' with boxes title "Po(4)"
set output "Po5.png"
plot 'po5' with boxes title "Po(5)"
set output "Po6.png"
plot 'po6' with boxes title "Po(6)"
set output "Po7.png"
plot 'po7' with boxes title "Po(7)"
set output "Po8.png"
plot 'po8' with boxes title "Po(8)"
set output "Po9.png"
plot 'po9' with boxes title "Po(9)"
set output "Po10.png"
plot 'po10' with boxes title "Po(10)"