統計学復習メモ15: 幾何分布のパラメーターの最尤推定量

前のメモで間抜けなことをしたついでに、同じ問題についてもう少し考察する。

再現率が低いバグを、(1) Aさんは200回試行して1回発生させ、Bさんは500回試行して1回発生させ、Cさんは1000回試行して1回発生させた場合と、(2) Aさんは200回目で1回発生させ、Bさんは500回目で1回発生させ、Cさんは1000回目で発生させた場合とでは当然数字の意味が異なる。(1)では発生させた後も試行してる可能性があるからである。

発生させたら試行を終了すると考えた場合、発生率をpとすると、k回目で発生する確率は、(k-1)回失敗して1回成功する確率なので、p(1-p)k-1である。簡単にするため、k+1回目で発生する確率をP(k)=p(1-p)kとする。このkの分布には「幾何分布」という名前がついているらしい。幾何級数（等比級数）だからということらしいが、この用語は一般に通じるものなのかどうか疑問だが、今回はこの用語を使う。発生するまでの試行回数の標本X1〜Xnが得られた時、それが幾何分布に従うとすると、発生率pの推定量は何になるだろうか？

前回に続き、最尤推定法を使う。幾何分布の確率をθ、尤度関数（結合確率）をL(θ)とすると、
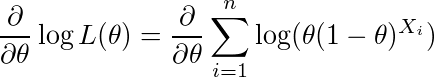
¥frac{¥partial}{¥partial¥theta}¥log L(¥theta) = ¥frac{¥partial}{¥partial¥theta}¥sum_{i=1}^{n}¥log(¥theta(1-¥theta)^{X_i})
なので、これが0になるθを求める。
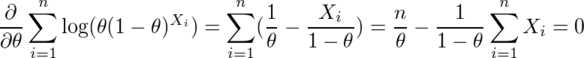
¥frac{¥partial}{¥partial¥theta}¥sum_{i=1}^{n}¥log(¥theta(1-¥theta)^{X_i})=¥sum_{i=1}^{n}(¥frac{1}{¥theta}-¥frac{X_i}{1-¥theta})=¥frac{n}{¥theta}-¥frac{1}{1-¥theta}¥sum_{i=1}^{n}X_i=0
で
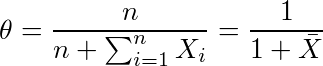
¥theta=¥frac{n}{n+¥sum_{i=1}^{n}X_i}=¥frac{1}{1+¥bar{X}}
となる。

従って、上記(2)の場合だと、X1=199, X2=499, X3=999なので、p=3/1700と推定される。
(1)の場合は、前のメモの通り、(1/200+1/500+1/1000)/3=1/375が妥当だと思う。