Coupon collector's problem

問１：おまけとしてフィギュアか何かが入っているお菓子があるとする。おまけは全ｍ種類あり、お菓子の購入時にはどれが入っているかわからないとし、ｍ種類は同じ確率で入っているとする。このお菓子をｎ回買うと、おまけが全種類揃う確率はいくらか？


これはTV東京の「ミネルヴァの法則」という昔の番組で出てきた問題のアレンジである。番組での問題は、おまけは10種類だと、100回買うと99%以上の確率で全種類揃うか（○／×）、という感じだったと思う。これの正解発表の時に、全種類揃う確率が99%になるのは66回であると、計算方法抜きで出てきた。

大学を卒業し、数式の類から遠ざかって10年以上、数学力はすっかり鈍っていたとはいえ、大学は理系卒で、高校時代は確率が得意中の得意だった身である。たかがテレビに出てくる確率の問題が解けないはずが無いと思って、その66を計算で求めようとしたが、やり方がわからず、その番組を見た日からのべ10時間以上考えて降参した。

三十半ばで再び数学に目覚めて１年、紙の上で数式をぐりぐりする右手を取り戻して、やっと解けた。


答１：
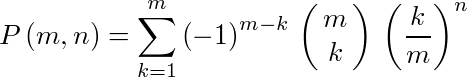
P¥left( m,n¥right) =¥sum_{k=1}^{m}{¥left( -1¥right) }^{m-k}¥,¥pmatrix{m¥cr k}¥,{¥left( ¥frac{k}{m}¥right) }^{n}
または
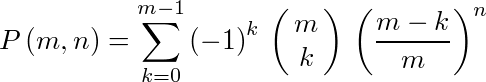
P¥left( m,n¥right) =¥sum_{k=0}^{m-1}{¥left( -1¥right) }^{k}¥,¥pmatrix{m¥cr k}¥,{¥left( ¥frac{m-k}{m}¥right) }^{n}
（これらはΣを展開すると同じ式、(m k)が縦に並んでるのは組み合わせ（mCkと書くのと同じ））


解説を試みる。

n個買うと、結果のパターンはmn通りである。この内、m種類揃っているのは、(m-1)種類以下しか無い場合を引いたものである。
(m-1)種類しか無いパターンは、（無い1種類のパターンmC1）×（(m-1)種をn回選ぶパターン(m-1)n）、(m-2)種類しか無いパターンは、（無い2種類のパターンmC2）×（(m-2)種をn回選ぶパターン(m-2)n）、…のように計算できると簡単なのだが、そうはならない。例えば(m-1)nパターンの中にも(m-2)種類以下しか無いパターンが含まれてしまうからだ。

この問題には「包除原理」(Inclusion-exclusion principle)というのが使えて、正しくは、(m-1)種類以下しか無いパターンの数は
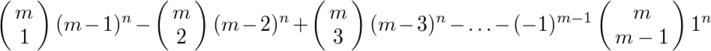
¥pmatrix{m¥cr 1}(m-1)^n - ¥pmatrix{m¥cr 2}(m-2)^n + ¥pmatrix{m¥cr 3}(m-3)^n - ¥ldots - (-1)^{m-1}¥pmatrix{m¥cr m-1}1^n
であり、従ってm種類あるパターンの数はm^n(=mC0 m^n)からこれを引いたもの、
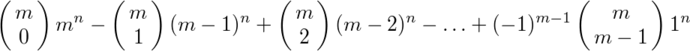
¥pmatrix{m¥cr 0}m^n - ¥pmatrix{m¥cr 1}(m-1)^n + ¥pmatrix{m¥cr 2}(m-2)^n - ¥ldots + (-1)^{m-1}¥pmatrix{m¥cr m-1}1^n
という＋と−が交互に出てくる和になる。これを全てのパターンの数m^nで割ってΣ記号で整理したのが上記の答である。

この問題に「包除原理」が使えることを理解するには、勘が冴えてれば何も要らないかも知れないが、勘が鈍い日は次のように考えてはどうだろうか。
包除原理とは、例えばn人の人がいて、A,B,Cの3つの特徴を調べ、1人の人が複数の特徴を持つことができる時、いずれの特徴も持たない人の数が、
全体の人数−（Aの人数+Bの人数+Cの人数）＋（AかつBの人数＋BかつCの人数＋CかつAの人数）−（AかつBかつCの人数）
となるようなことを言うものである。なぜそのようになるかというと、

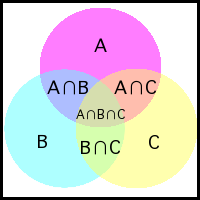
この図の白い部分が求める人数だが、全体から1つの特徴を満たす人数を引くと2つの特徴を持つ人を2回引くことになり、引き過ぎた分を足すために2つの特徴を満たす人数を足すと3つの特徴を持つ人を3回足すことになり（m個の特徴を持つ人は(m-1)個の特徴を持つ人としてm回数えられるため）、以下同様に全ての特徴を満たす人数まで相殺する必要があるからである。
話を戻して、m種類のおまけが揃うパターンの数を求めるには、おまけ1が欠けてる場合をA、おまけ2が欠けてる場合をB、おまけ3が欠けてる場合をC、…と考えると、AとBが同時に起こることもあるから、A,B,…は上の図のように重なるので、どれも欠けていない場合、すなわち上の図の白い部分の数を数えようとすると、必然的に包除原理のような計算になるのである。


さて、現実的には、何個買った時にコンプリートしてる確率がいくらになるかより、大体何個買ったらコンプリートできるか、すなわち、コンプリートするまでの回数の期待値の方が興味があるのではなかろうか。

問２：おまけが全種類揃うまでのｎの期待値は？

この問題は、"Coupon collector's problem"と呼ばれるらしい。日本語訳は不明だが、「食玩問題」とか「クーポン収集問題」とか呼ばれることがあるようだ。
確率分布がP(X)の確率変数Xの期待値E(X)を求める公式はΣ(X P(X))であり、上のP(m,n)より、n回目にm個揃う確率がP(m,n)-P(m,n-1)なので、nの期待値E(N,m)（以降、E(m)と省略する）はΣ(n (P(m,n)-P(m,n-1)))である。コンピューターでそれなりに大きなnまで計算すると正しい値に近づくので、一応正しい式のようであるが、これを解こうとするとひどい目に遭う。
しかし、違う発想で解くと、かなり簡単に求められる。


答２：
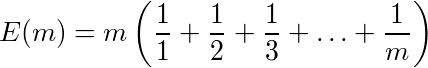
E(m)=m¥left(¥frac{1}{1}+¥frac{1}{2}+¥frac{1}{3}+¥ldots+¥frac{1}{m}¥right)


k-1種類まで揃ってから、k種類目が得られるまでに、平均何回かかるかと考える。
まだ得られてないのは(m-k+1)種類なので、1回買ってまだ得られてないのが得られる確率pは、p=(m-k+1)/mである。当たりの確率がpの時、当たりを引くまでの回数は、幾何分布に従う。すなわち、x回目で当たる確率はP(x)=(1-p)^(x-1) pである。このxの平均はΣxP(x)であり、等比級数の和を求める要領で解くと、ΣxP(x)=1/pとなる。従って、k種類まで揃ってからk+1種類目が得られるまでの回数の期待値はm/(m-k+1)である。
E(m)はこれを1種類目からm種類目まで足したものだから、
E(m)=m/m + m/(m-1) + m/(m-2) + ... + m/(m-m+1) = m(1/1 + 1/2 + ... + 1/m)
となる。

参考：
E(10)≒29
E(15)≒50
E(20)≒72
E(25)≒95
E(100)≒519

ちなみに、オイラー定数というのを使うと、
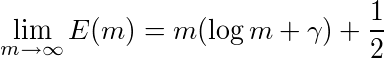
¥lim_{m¥rightarrow¥infty}E(m)=m(¥log m + ¥gamma) + ¥frac{1}{2}
（γはオイラー定数、0.5772...）なのだそうだ。


Maximaでの計算例

P(m,n) := sum((-1)^(m-k) * binomial(m,k) * (k/m)^n, k, 1, m);
P(10,64),numer;
P(10,65),numer;
P(10,66),numer;
(%o2) .9882380477442749
(%o3) .9894114212010926
(%o4) .9904680213733168

P(m,n) := sum((-1)^k * binomial(m,k) * (1-k/m)^n, k, 0, m-1);
P(10,64),numer;
P(10,65),numer;
P(10,66),numer;
(%o6) .9882380477442749
(%o7) .9894114212010927
(%o8) .9904680213733169

E(m) := sum(n*(P(m,n)-P(m,n-1)), n, m, 1000);
E(100),numer;
(%o10) 513.9447816215018 /*1000項目くらいまででは十分に収束せず*/

E(m):=m*sum(1/k,k,1,m);
E(100),numer;
(%o12) 518.737751763962 /*これが正しい値*/

n: [10,15,20,25,30,100];
for i:1 thru 6 do print(float(E(n[i])));
(%o13) [10,15,20,25,30,100]
29.28968253968254
49.7734348984349
71.95479314287364
95.39895444383767
119.8496139276117
518.737751763962

E(m):=m*(log(m)+%gamma)+1/2;
for i:1 thru 6 do print(float(E(n[i])));
(%o15) E(m):=m*(log(m)+%gamma)+1/2
29.29800757895579
49.77898799005614
71.95895876911047
95.40228724424334
119.8523913969106
518.7385850889625