問：ｎ個の箱にそれぞれ異なる額のお金が入っており、どれか１つの箱のお金をもらえるとする。最大の金額は不明である。１つ箱を開けたら、そのお金をもらって終了する（残りの箱は開けない）か、そのお金をパスするかを決めないといけない。１度パスしたお金はもらえない。最高額を得る確率を最大にするには、どのように箱を選択すれば良いか。
前項と同じく、「ミネルヴァの法則」の問題のアレンジである。番組の問題では、n=20だった。正解は、最初の37%（=7個）の箱は開けても選択せず、次に出てきた、それまでの最高額より大きい金額を選択するというものである。
前項の問題と同様、たかがテレビに出てくる確率の問題が解けないはずが無いと思って、その37%を（中略）降参した。
この度、やっと解けた。
答：最初のn/e個（eは自然対数、小数点以下切り捨て）の箱の中身をパスして、次に出てきた、それまでの最高額より大きいものを選択する。
解説する。
考えられる手順は、最初のｒ個の箱の中身をパスして、次に出てきた、それまでの最高額より大きいものを選択する、という手順に帰着する。これ以外を考えても無駄であることは容易にわかる（注：ここでの問題では最高額以外は全て外れである）。従って、その適切なｒを選ぶのが問題である。
r個をパスして最高額が得られる確率をP(r)とする。最高額がx番目(x>r)にあり、それを選択できる確率は、
・最高額がx番目にある確率＝1/n
・1〜r番目の最大より大きな額が(r+1)〜(x-1)番目には無い確率＝1〜(x-1)番目の最大が1〜r番目に出てくる確率＝r/(x-1)
の積である。P(r)はそれを全てのxについて足し合わせたものなので、
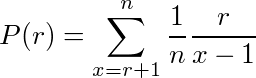
となる。
P(r)が最大になるrを求める前に、P(r+1)-P(r)を計算して、P(r)の増減を調べてみる。
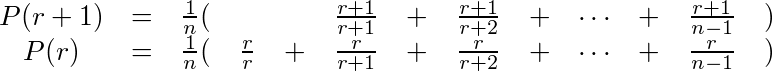
なので、上から下を引いて、
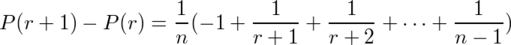...(1)
である。これはよく見るとrが大きくなると項が減る一方で、どこかで0より小さくなる。従って、P(r)が最大になるのは、P(r)が減り始める直前のr、すなわちP(r+1)-P(r)<0となるrである。(1)の右辺の括弧内に注目すると、
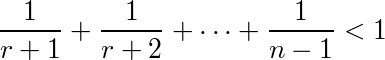...(2)
となる最小のrとも言える。
さらに、nが十分大きいとして、(2)の左辺を計算し易い積分に近似する。区分求積法より、
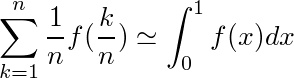
なので、f(x)=1/xとして積分範囲を調節すると、
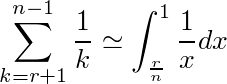
と近似できる。右辺<1を計算すると、-log(r/n)<1であり、r/n>1/eすなわちr>n/eが求まる。n/eは整数ではなく、r>n/eの整数だとP(r)がちょっと減るので、n/eを超えない整数がP(r)を最大にするrである。（nが小さい時は(2)で検算した方が良いかも知れない）
37%とは、1/e(≒0.368)のことであった。
なお、この問題は(classical) secretary problemと呼ばれ、問題の解は37%の法則とか37%ルールとかと呼ばれるらしい。
事象の全体の数nがわからないという場合は、その事象が時間当たりに発生する確率が一定と考えていいなら、期限をTとし、T/eまでに発生した最高のものより良い事象が起これば選択する、としても良い。
この法則はお見合いにも応用できると言う人がいるが、お見合いでは選んだ相手がOKしてくれるとは限らないのは言うまでもない。
コメント