あるソフトウェアをバージョンアップしたら、処理時間が少し伸びた。
計測結果は、次のような感じだった。
| 入力データ | 処理時間(before) | 処理時間(after) |
|---|---|---|
| 1 | 300 | 360 |
| 2 | 200 | 180 |
| 3 | 100 | 120 |
| 4 | 500 | 480 |
| 5 | 400 | 440 |
| 6 | 1200 | 1300 |
| 7 | 250 | 270 |
| 8 | 200 | 210 |
| 9 | 1500 | 1800 |
| 10 | 1000 | 1100 |
ぱっと見で明らかに悪化しているが、念の為、統計学的に有意な差であることを示しておこうと思って、Excelの分析ツールの「t検定: 一対の標本による平均の検定」(いわゆる対応のあるt検定)を使ったら、p値が意外と小さくなかった。例えば上記のデータだと両側検定で0.0706となる。
それでも、有意水準を10%とすると有意差ありと言えないことはないので、不本意ながらその結果を付けて報告した。
そのメールを発信した日の帰り道に、このt検定は妥当な計算がなされていないのではないかと疑問に思った。 同じ入力データのセットを使ったのでbeforeとafterで対応があるが、入力データはサイズがまちまちなので、(after-before)の差それぞれは同列に扱えない。(after-before)の単純な差でなく、差分の比率、それぞれ何%増であるかが検定の対象である。 専門的に言うと、t検定は標本の母集団が正規分布に従うのが前提であるが、この(after-before)の差は正規分布に従うはずがないので、t検定を用いるのは不適切だということになるだろう。
もしかして、Excelの分析ツールの「t検定: 一対の標本による平均の検定」はそれも考慮したp値を計算してたりしないだろうか、と期待したが、結果を確かめてみると、一般的な「対応のあるt検定」と同様、
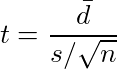
(dは対応のある数値の差、dの上のバーは平均、sは不偏標準偏差、nは標本データ数)
というt値と、それに対応する自由度n-1のt分布における外側確率だった。
こういった、差分の比率を検定したいケースはよくあると思うので、何か定番の方法があるのではないかと思って少し探したが、全く見つからなかった。
対応するデータの差分を、正規分布に従うように補正(正規化)してt検定すれば良いのだが、よく考えると、一般的には差分をbeforeの値で割ったものが正規分布に従う保証は無いのである。今回のデータが、計算量が入力データのサイズに比例する処理時間であることがわかっているから、差分をbeforeで割ったら大よそ正規分布に従うという仮定を置けるが、もし計算量のオーダーがO(n)でなくO(n2)だったら、差分のオーダーもO(n2)ならbeforeの平方根で割るべきかも知れないし、差分のオーダーが不明なら正規化のしようが無いかも知れない。
今回は結局、対応するデータの差をbeforeとafterの平均で割ることによって正規化し、t検定をやり直した。単純にbeforeの値で割って正規化しても良いだろうが、before→afterとafter→beforeを対称に扱う為、例えば80→100と100→80が相殺されるようにする為にこのようにした。考え過ぎか。
例えば上記のデータだと、このように正規化して計算すると、両側検定のp値が0.0267となる。
なお、対応のあるt検定は、中心極限定理により、標本数nが多い時には対応するデータの差が正規分布に従わなくても問題ないという話があるようだ。
今回のデータはn=10しか無かったのでp値に大きな差が出たが、そういうのは稀で、通常はこんなことを考える必要が無いということなのだろうか。
今回の計算に用いたPythonのコードと出力結果を貼り付ける。
コード
from scipy import stats
data1 = [300, 200, 100, 500, 400, 1200, 250, 200, 1500, 1000]
data2 = [360, 180, 120, 480, 440, 1300, 270, 210, 1800, 1100]
data3 = [(data2[i] - data1[i]) * 2 / (data1[i] + data2[i]) for i in range(len(data1))]
t, p = stats.ttest_rel(data1, data2)
print("t =", t, ", p =" ,p)
print(stats.ttest_1samp(data3, 0))
t = -2.0499778867533394 , p = 0.07061628029469634 Ttest_1sampResult(statistic=-2.644247535724081, pvalue=0.026727030549217334)
コメント