ディリクレ分布を直観的に理解する

サイコロを振って1,2,3,4,5,6の目が出た回数がそれぞれn1,n2,n3,n4,n5,n6だった時、それぞれの目が出る確率p1,p2,p3,p4,p5,p6は(n1,n2,n3,n4,n5,n6)をパラメーターとするディレクトリ分布に従う、という話を聞いたので、ちょっと勉強しておくことにした。

コインの表が出る確率がpの時、N回振って表が出る回数nはNとpをパラメーターとする二項分布に従う。
コインをN回振って表が出た回数がn回だと観測された時、点推定では表が出る確率はn/Nとなるが、ベイズ推定では表が出る確率（事後確率）pは(n+1, N-n+1)をパラメーターとするベータ分布に従う。
勝手な表記だが、回数がnになる確率P(n)が
P(n;N,p)=Binomial\_PMF(n;N,p)=\pmatrix{N \cr n}p^n(1-p)^{N-n}
(PMF=Probability mass function)という感じであり、事後確率がpになる確率の密度関数f(p)が
f(p;N,n)=Beta\_PDF(p;n+1,N-n+1)=\frac{\Gamma(N+1)}{\Gamma(n+1)\Gamma(N-n+1)}p^n(1-p)^{N-n}=\pmatrix{N \cr n}p^n(1-p)^{N-n}
(PDF: probability density function)ということになる。
この関係のことを、ベイズ推定の用語で、尤度関数が二項分布の場合、ベータ分布は共役事前分布(conjugate prior)であると言うらしい。

多項分布とディリクレ分布もその関係にある。
サイコロをN回振って1〜6の目が出る確率がp1〜p6の時、1〜6の目が出る回数n1〜n6はp1〜p6をパラメーターとする多項分布に従う。(n1+n2+n3+n4+n5+n6=N, p1+p2+p3+p4+p5+p6=1)
サイコロをN回振って1〜6の目が出た回数がそれぞれn1〜n6回だと観測された時、推定される1〜6の目が出る事後確率p1〜p6は(n1+1, n2+1, n3+1, n4+1, n5+1, n6+1)をパラメーターとするディリクレ分布に従う。
nをn1〜n6のベクトル、pをp1〜p6のベクトルとすると、回数がnになる確率P(n)が
P(n;p)=Multinomial\_PMF(n;p)=\frac{\left(\sum_{k=1}^{6}n_k\right)!}{\prod_{k=1}^{6}n_k!}\prod_{k=1}^{6}p_k^{n_k}
であり、事後確率がpになる確率の密度関数f(p)が
f(p;n)=Dirichlet\_PDF(p;n+1)=\frac{\Gamma\left((\sum_{k=1}^6n_k)+1\right)}{\prod_{k=1}^6\Gamma(n_k+1)}\prod_{k=1}^6p_k^{n_k}=\frac{\left(\sum_{k=1}^6n_k\right)!}{\prod_{k=1}^6n_k!}\prod_{k=1}^6p_k^{n_k}
ということである。

ディリクレ分布はベータ分布の確率変数の次元を拡張したものである。
上記のコインの例も多項分布とディリクレ分布で表現でき、コインの表が出る確率がp1、裏が出る確率がp2の時、N回振って表が出る回数n1と裏が出る確率n2は(p1, p2)をパラメーターとする多項分布に従う。
コインをN回振って表が出た回数n1回、裏が出た回数がn2だと観測された時、表が出る事後確率p1、裏が出る事後確率p2は(n1+1, n2+1)をパラメーターとするディリクレ分布に従う。

図1はパラメーターを(3n+1, 2n+1)、n=1〜10としたベータ分布のグラフである。 コインを投げて5回中3回、10回中6回、15回中9回、...、50回中30回、表が出た時の表が出る確率の分布に対応する。
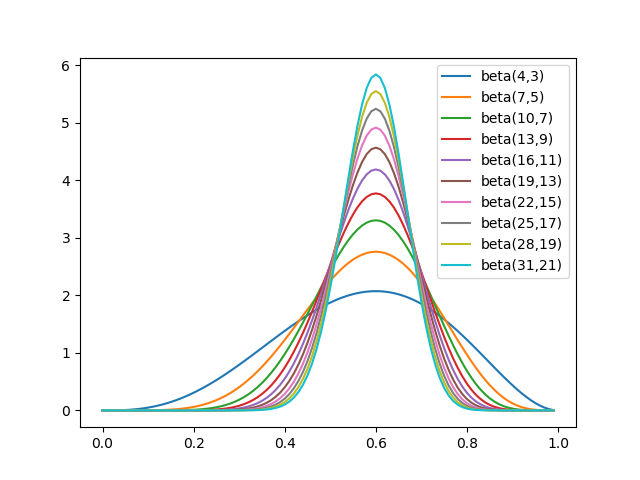図1
5回中3回でも表が出る確率が0.6である確率が最も高いが、他の確率である確率もそれなりに高いのに対し、回数を増すほど確率が0.6近辺に限定されていく様子がわかる。
最尤推定のような点推定では5回中3回でも50回中30回でも単に0.6であり、その尤もらしさが区別されない。

図2は同様にパラメーターを(3n+1, n+1)、n=1〜10としたベータ分布のグラフである。 コインを投げて4回中3回、8回中6回、...、40回中30回、表が出た時の表が出る確率の分布に対応する。 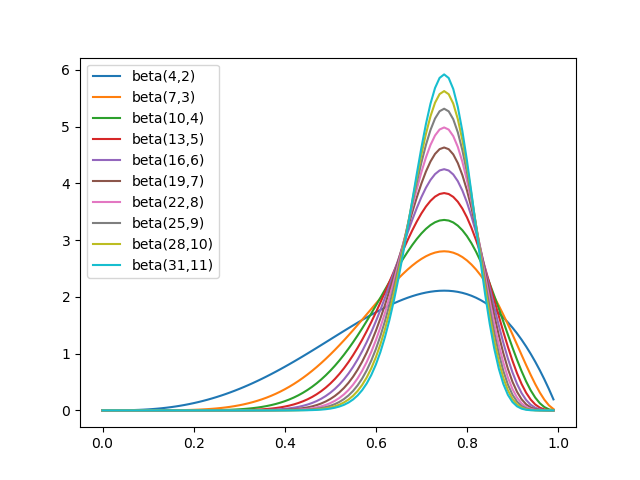図2

図3はパラメーターを(2+1, 3+1, 5+1)とした3次元のディリクレ分布のグラフである。 ３面しか無いサイコロを10回振って各面が2回、3回、5回出た時の各面が出る確率の分布に相当する。
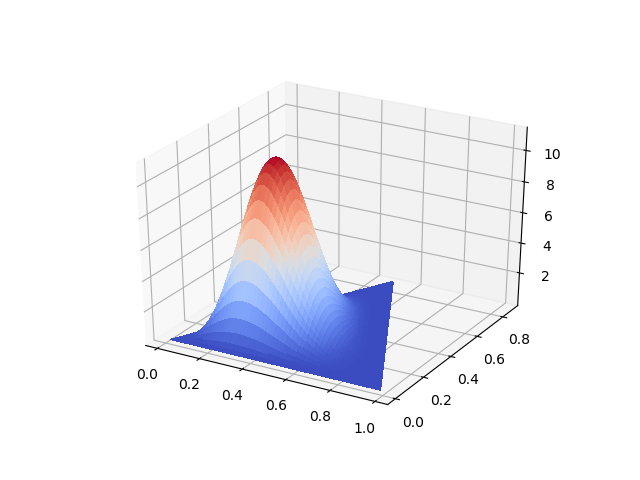図3
ちょっとややこしいが、三角形の各頂点がサイコロの各面に対応し、三角形内の各頂点への近さが各面の出る確率に対応し、上方向の高さがその確率の組み合わせになる確率であり、高いほど高温の色になっている。右下の頂点が1つ目の面、右上の頂点が2つ目の面、左の頂点が3つ目の面に対応する。XYZ空間で右下の頂点が(1,0,0)、右上の頂点が(0,1,0)、左の頂点が(0,0,1)にあるとすれば、三角形内の点のX座標、Y座標、Z座標が各面の出る確率である。
上から見ると、図4のようなヒートマップになる。
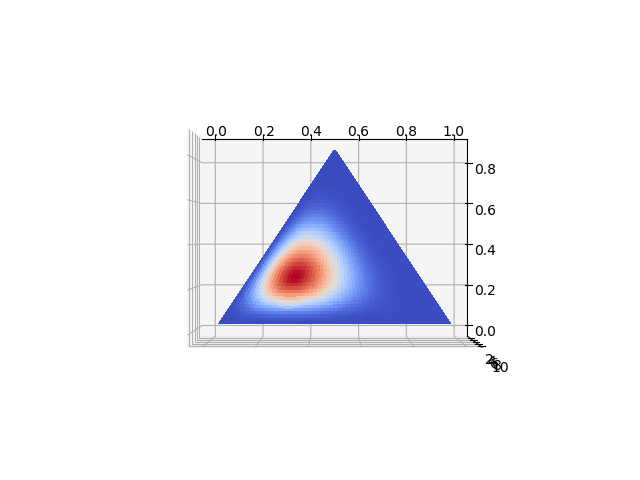図4
(0.2, 0.3, 0.5)に対応しそうな所が頂点になっている。

図5はパラメーターを(20+1, 30+1, 50+1)とした3次元のディリクレ分布のグラフである。 ３面しか無いサイコロを100回振って各面が20回、30回、50回出た時の各面が出る確率の分布に相当する。
図5
図6は上から見た図である。
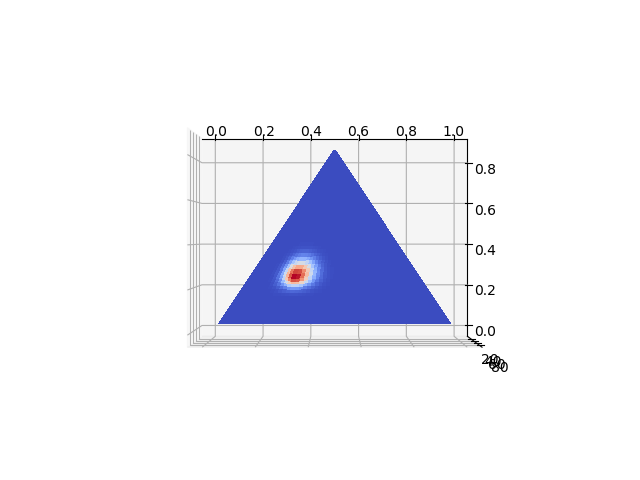図6
それぞれの面が出た割合が同じでも、回数を重ねた方が確率が高い範囲が限定される様子がわかる。

図1〜図6はPython + matplotlibで作成した。

■図1のソースコード 
import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

X = np.arange(0, 1, 0.01)
for i in range(1, 11):	# gives 1-10
    a = 3*i + 1
    b = 2*i + 1
    be = beta(a=a, b=b)
    plt.plot(X, be.pdf(X), label='beta({},{})'.format(a,b))

plt.legend()
plt.show()
■図5のソースコード 
import numpy as np
from scipy.stats import dirichlet
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

fig = plt.figure()
ax = fig.gca(projection='3d')

# triangle mesh grid (0,0)-(1,0)-(0,1)
xx = np.array([[0.01*a*0.01*(100-b) for a in range(1, 100)] for b in range(1, 100)])
yy = np.array([[0.01*b] * 99 for b in range(1, 100)])

# Dirichlet PDF on mesh grid ((0,0)->(0,0,1), (1,0)->(1,0,0), (0,1)->(0,1,0))
a, b, c = (2, 3, 5)
di = dirichlet([a+1, b+1, c+1])
Z = di.pdf([xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

# transform isosceles right triangle mesh into equilateral triangle
xx2 = np.array([x + (0.5 - np.average(x)) for x in xx])
yy2 = yy * np.sqrt(3) / 2

# 3D plot
ax.plot_surface(xx2, yy2, Z, cmap=cm.coolwarm, antialiased=False)
plt.show()

このような３次元のディリクレ分布のグラフは、Wikipediaを始め色々な所にあり、MATLABで描画するサンプルコードは見つかったが、Pythonで綺麗に描画するサンプルコードが見つからなかったので、無理矢理作ってみた。
mpl_toolkits.mplot3d.Axes3D.plot_surfaceを使う為に、下図の上側のようなmesh gridを下側のように三角形に潰している。

これによって丁度、X座標とY座標の値が三角形の"Barycentric coordinate system"の2つの頂点の重みになるので、コードが幾分シンプルになった。