統計学復習メモ10: なぜ共分散行列の固有ベクトルが単位主成分なのか

前項に書いた通り、主成分分析における主成分の単位ベクトルは、共分散行列の固有ベクトルとして求まる。そのこと自体に昔から興味があったので、主成分分析の復習ついでに考察してみる。

まず、最小２乗法で考えてみる。簡単のために２次元で考える。ｎ個のサンプルデータを

とし、第１主成分の単位ベクトルを

とすると、Xに対応する主成分軸上の第１主成分Yは
Y=P^TX
であり、そのYを元の座標系に戻したものX~は
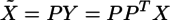
¥tilde{X}=PY=PP^TX
である。このことは、高校で習った一次変換を思い出してやってみるとわかる。このX~が、Xを第１主成分の軸上に射影したものであり、これとXとの距離が、最小にしたい誤差ということになる。その誤差Eを、Xを直交座標とした場合の距離の２乗とすると、
E=(\tilde{X}-X)^T(\tilde{X}-X)=\sum_{i=1}^n\|\tilde{X}_i-X_i\|^2
であり、p12+p22=1に注意すると、これは
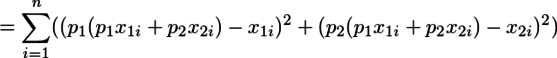
=¥sum_{i=1}^n((p_1(p_1x_{1i}+p_2x_{2i})-x_{1i})^2+(p_2(p_1x_{1i}+p_2x_{2i})-x_{2i})^2)
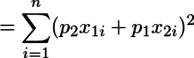
=¥sum_{i=1}^n(p_2x_{1i}+p_1x_{2i})^2
と計算できる。

このp1とp2の２次関数であるEの最小値ををp12+p22=1の条件下で求めるので、「ラグランジュの未定乗数法」というやつを使う。すると、G=p12+p12-1と置くと、

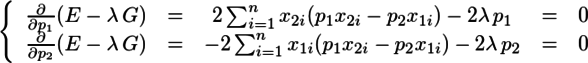
である。これを整理すると、

となる。これの最初の行列は、よく見ると、Xの共分散行列

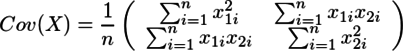
の逆行列のスカラー倍であるので、上の方程式は、両辺に左側からCov(X)をかけると

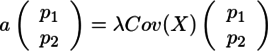
（aはスカラー）となり、a/λをλと置き直すと、

が得られる。従って、固有ベクトルの定義より、PはCov(X)の固有ベクトルであることがわかる。


さて、Xが２次元の場合については辛うじて求まったが、Xが３次元になると、この方法ではEが複雑になり、非常に辛い。筆者はMaximaに式の変形をさせながら３次元についても同じであることを調べようとしたが、E-λGを偏微分した所で変数が目測で200個以上ある状態になり、なんとなく雰囲気はあったが挫折した。この方法ではXをｍ次元に一般化するのはかなり困難か、何か特殊な技術が必要だと思う。

そこで、次に分散最大で考えてみる。こちらは幾分容易である。
ｎ個のサンプルデータを

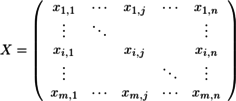
とし、第１主成分の単位ベクトルを

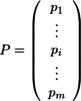
として、第１主成分

の分散
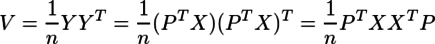
V=¥frac{1}{n}YY^T=¥frac{1}{n}(P^TX)(P^TX)^T=¥frac{1}{n}P^TXX^TP
を最大にするPを求めることを考える。Xのi行目とj行目の共分散をcov(Xi,Xj)と書くと、
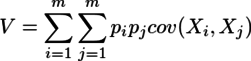
V=¥sum_{i=1}^{m}¥sum_{j=1}^{m}p_ip_jcov(X_i,X_j)
とも書ける。このp1...pmの２次関数であるVの最大値をp12+p22+...+pm2=1の条件下で求めるので、やはりラグランジュの未定乗数法を使う。すると、G=p12+p22...+pm2-1と置くと、

である。これを整理すると、

すなわち

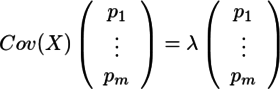
が得られ、PがCov(X)の固有ベクトルであることがわかる。

第２主成分以降についても、それより前の主成分と直交するという条件を加えて、同様の方法で解くと、やはりCov(X)の固有ベクトルであることがわかり、第１主成分から順番に分散最大の固有値が取られていくので、第k主成分はCov(X)のk番目に大きい固有値に対応する固有ベクトルだと求まる。

主成分の単位ベクトルが共分散行列の固有ベクトルとして求まることを確かめるだけなら、もっとシンプルな方法があるのをWikipediaで見つけた。

Pを、単位主成分を横に並べたもの

とし、YをXの主成分とすると、
Y=P^TX
なので、Yの共分散行列は
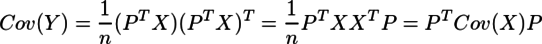
Cov(Y)=¥frac{1}{n}(P^TX)(P^TX)^T=¥frac{1}{n}P^TXX^TP=P^TCov(X)P
である。

ここで、Pが直交行列（正規直交基底）なので
P^T=P^{-1}
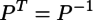
であることと、Yが主成分なのでYの各行の間には相関が無い（主成分分析の主成分軸はそのように取っている）ため、Yの共分散行列の対角成分以外は0である（対角成分は分散、それ以外は共分散だから）こと、すなわち、Cov(Y)は

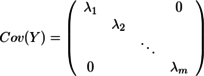
と置けることを使う。

P^T=P^{-1}
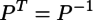
だから、上のCov(Y)の関係式はP Cov(Y) = Cov(X) Pと変形でき、PとCov(Y)を展開すると

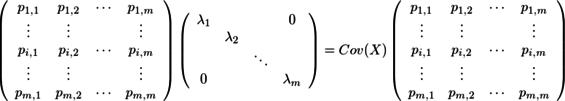
となり、さらに両辺を列毎にばらすと

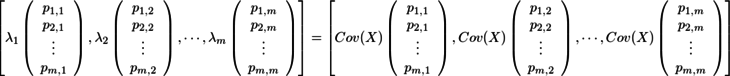
となり、両辺の各列を比較すると、Pの各列がCov(X)の固有ベクトルであることがわかる。


こういう裏技があるのも、主成分分析というものが数学的に綺麗だからなのだろうか。

もっとも、筆者は本文に書いたような最小２乗法や分散最大の計算をする前にこれを見つけていたのだが、最初は意味が分からなかった。普段から行列に慣れ親しんでるか、筆者のように１ヶ月くらい考え続けて頭の中が行列まみれにならないと、なかなか納得できないもののような気がする。
がしかし、わかってみると、単純なことだと思う。何で１ヶ月も理解できなかったのだろう。人間の脳は行列に慣れるのに時間がかかるのだろうか。それとも、わかってる人に教えてもらったら３日で理解できたのだろうか。