前々項に書いたように、主成分分析は特異値分解を使っても計算できる。なぜだろうか。
それについても答えを得たので、ついでにメモしておく。
n個のサンプルデータを横に並べたものを
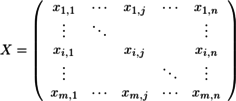
(m<n)とし、Pを単位主成分を横に並べたもの

とし、YをXの主成分とすると、

である。
特異値分解定理により、Xは何らかの正規直交行列U,Vと、m行m列部分が対角行列でそれ以外が0である行列Σによって、

と分解される。それを応用すると、
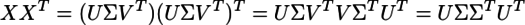 ...(1)
...(1)
が成り立つ。XXTはm×mの正方行列なので、ΣΣTもm×mの正方行列であり、
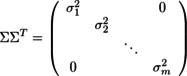 ...(2)
...(2)
と置くことができる。(σ1≧σ2≧...≧σmである)
前項に書いたように、Yの共分散行列は
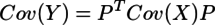
であり、従って
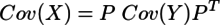
であり、Cov(Y)はCov(X)の固有値を対角成分に持つ行列である。Cov(Y)=Λを
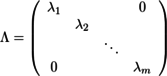
(λ1≧λ2≧...≧λm)と置くと、
 ...(3)
...(3)
となる。一方、
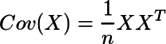
なので、(1)と(2)を使うと、
 ...(4)
...(4)
という形にすることができ、(3)と(4)を見比べると、PもUも正規直交行列なので、U=P、
 すなわち
すなわち 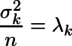
の関係があることがわかる。さらに、
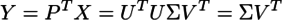
なので、Xの主成分YはXを特異値分解したものの一部として求められることがわかる。
記号で書くと 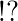 という感じであるのは筆者だけであろうか。固有値・固有ベクトルと特異値分解とにこんな見事な関係があるとは、さすが主成分分析である。
という感じであるのは筆者だけであろうか。固有値・固有ベクトルと特異値分解とにこんな見事な関係があるとは、さすが主成分分析である。
ちなみに、正方行列Aを、その固有ベクトル行列Wと固有値行列Λを使って
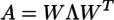
と分解することを、スペクトル分解と言うらしい。主成分は、特異値分解またはスペクトル分解を使って求められるということになる。
コメント