以前のエントリーにて実際にやってみたが、カイ2乗分布とカイ2乗検定に軽く触れてみると、χ2の定義が違うので混乱した。カイ2乗分布で定義されるχ2は
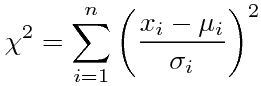
(xiは標本値、μiは平均、σiは標準偏差)であるのに対して、カイ2乗検定で使われるχ2は
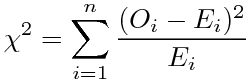
(Oは観測値(observed)、Eは期待値(expected)または理論値)である。何でそれらをχじゃなくわざわざχ2と置くんだ、ということも少し引っ掛かるが、それは分散のσ2の例もあるので、値の意味的にきっと何か2乗的、2乗系、2乗fulなんだろうと思って通り過ぎるとして、2つのχ2の式は関連がありそうに見えて何と何が対応するのかよくわからない。Σ内の分母は上のが分散なのに対して、下のは期待値である。分散で割るのと期待値で割るのは違うであろう。分母だけ見るからそう思うんだろうかと思ってΣ内全体を見ても、上のはお馴染みの(xが正規分布N(μ,σ2)に従う時の)標準正規分布N(0,1)に従う値の2乗であるし、下のは平均からの差の2乗を平均で割ってて、平均の大きさに比例しそうな、2乗的には見えない、奇妙な値である。まるで1つ期待値で割り忘れたかのような形をしている。
結論から書くと、上の2つの式は、何か対応がありそうな形はしているが、真正面からパーツ毎に対応させてようと考えるのはやめた方が良さそうだ。
落ち着いてWikipediaを眺めていると、「ピアソンのカイ2乗検定」という言葉が目に入った。カイ2乗検定というのも色々ある中で、以前のエントリーに書いた検定の例は、最もポピュラーな、ピアソンのカイ2乗検定というやつらしい。数学的に説明するのは大変難しいが、検定統計量
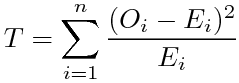
がカイ2乗分布に従うことがピアソンによって示されているので、カイ2乗分布を使って、この検定統計量がある値以上になる確率を知ることができるということだ。
Tは、各事象の実際の発生回数と期待値とのずれ(ばらつき)が大きいほど大きくなるので、観測されたTが十分低い確率でしか起こらないかどうか、すなわちそのばらつきが十分低い確率でしか起こらないかどうかを、このピアソンの方法で知ることができる。
逆に、実際の発生回数を真実、期待値を仮説とすると、Tが十分大きければ、もしその仮説が正しいとするとかなり稀なことが実際には起こったということになり、むしろその仮説が間違っていると考える方が合理的であるので、ある仮説を確率的に誤りと見なす(仮説を棄却する)のに使えるということである。
N(0,1)に従う標本の2乗和と、カイ2乗検定の検定統計量の両方がχ2と定義されるから、学ぶ人が混乱するんだ、と思うのは筆者だけだろうか。きっと何か合理的な理由があるんだろうが、それならその理由を先に知っておかないと混乱の元になると思うが、筆者には未だに見つけられていない。
コメント