統計学復習メモ12: 不偏推定量とは

以前にｔ分布を使うパラメーターの区間推定の方法を覚えたが、この前ちょっと推定の実践のネタを思いついてやってみようとしたら、そのパラメーターが正規分布に従うものではないことに気付き、１手目でつまずいた。これでは勉強した意味が無いと思い、推定というものの基礎を勉強し直すことにした。

区間推定をするにもまず、その区間の基準となる値（推定量）を点推定しないと始まらない。その点推定量が満たすのが好ましい性質として、不偏性と一致性がある。推定量θ^がパラメーターθの不偏推定量であるとは、
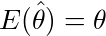E(¥hat{¥theta})=¥theta ...(1)
が成り立つことをいう。

出た E(¥hat{¥theta})=¥theta 。学生時代にこのθの上の屋根の意味が理解できなかったことが、私が推定・検定の１手目でつまずいた原因の１つであることは間違いない。そもそもなぜ統計学では推定するパラメーターをθと書くのか。高校の三角関数の授業で習って以来、私にとってはθといえば角度に違いないのであり、パラメーターをθと表すのは、円周率をxと表すとか、y=ax+bのxとyが定数でaとbがグラフの縦軸・横軸であるくらいの混乱の元である。

そもそも、θ^がθの推定値だとしたら、(1)が成り立たないとはどういう状態なのだろうか？それに、θが未知だからθを推定するのに、θ^の平均がθであることをどうやって確認するのか？
...という疑問を持ったのは筆者だけなのだろうか。

これは、θが確率変数のパラメーターであり、その推定量θ^を標本から求める方法を決めた時、仮にθによって決まる母集団からの標本を使った場合、θ^の平均がθに一致するなら、そのθ^は不偏推定量である、という意味らしい。

例題として、X₁〜X_nが平均μ、分散σ²の母集団からの標本として、まず標本平均X~=E(X)=1/n ΣX_iがμの不偏推定量かどうかを考える。
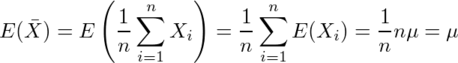
$E(¥bar{X})=E¥left(¥frac{1}{n}¥sum_{i=1}^{n}X_i¥right)=¥frac{1}{n}¥sum_{i=1}^{n}E(X_i)=¥frac{1}{n}n¥mu=¥mu$
従ってX~はμの不偏推定量である。

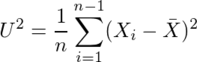次に、標本分散 $S^2=¥frac{1}{n}¥sum_{i=1}^{n}(X_i-¥bar{X})^2$ 、不偏分散 $U^2=¥frac{1}{n}¥sum_{i=1}^{n-1}(X_i-¥bar{X})^2$ がσ²の不偏推定量かどうかを考える。

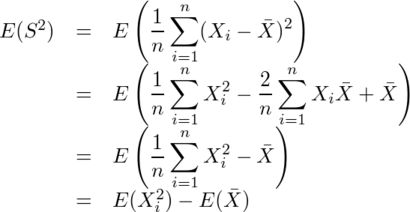
ここで、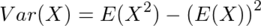 Var(X)=E(X^2)-¥left(E(X)¥right)^2 の公式と $Var(¥bar{X})=¥frac{1}{n}Var(X)$ の公式を用いると、
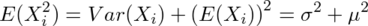
E(X_i^2)=Var(X_i)+¥left(E(X_i)¥right)^2=¥sigma^2+¥mu^2
$E(¥bar{X})=Var(¥bar{X})+¥left(E(¥bar{X})¥right)^2=¥frac{¥sigma^2}{n}+¥mu^2$
が求まるので、
$E(S^2)=¥frac{n-1}{n}¥sigma^2$
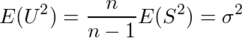
$E(U^2)=¥frac{n}{n-1}E(S^2)=¥sigma^2$
となる。従って、S²はσ²の不偏推定量ではなく、U²はσ²の不偏推定量である。