統計学復習メモ9: 主成分分析の計算方法

主成分分析の話になると大抵、固有ベクトルか特異値分解のどちらかが出てくる。主成分の単位ベクトルが固有ベクトルとして直ちに求められ、主成分の大きさが特異値分解を使って直ちに求められるからだ。

それにしても、行列には固有値や固有ベクトルがあるというのも、統計には分散や共分散があるというのも、理系の大卒なら誰でも知ってることだろうが、「共分散行列の固有ベクトルが主成分の単位ベクトルになる」と言われると、全く関係ない３つのものが突然シンプルに組み合わせられた感じで、衝撃的である。まるで
e^{-i¥pi}=-1
のような神秘的なものを感じるのは筆者だけだろうか。

そのこと自体は、至る所に証明というか説明があり、その方法も幾通りもある。基本的には、あるデータのど真ん中を通る直線として、最小２乗法のように２乗誤差を最小にする直線を求める代わりに、その直線方向の分散が最大になる（その直線上に射影した場合の分散が最大になる）直線を求める、という考え方である。そう言われればそういう考え方もありかな？とも思ったりするし、やっぱり最小２乗法で求める方がいいんじゃないの？とも思ったりするが、結局、主成分は分散最大で求めても最小２乗法で求めても同じ結果になるらしい。


とりあえず、固有ベクトル計算でやってみる。
m次元のデータn個を

（iは標本番号、pはパラメーター番号の意味）とし、共分散行列の固有値を

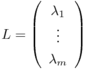
とし、対応する固有ベクトルを

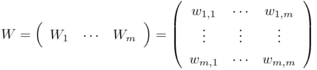
とすると、W1〜Wmが第１主成分〜第ｍ主成分、λ1〜λmがそれぞれの寄与率となる。
X,Wは行列である。プログラミング用語の「待ち行列」とかのqueueではなく、線形代数のmatrixである。フフン、行列くらい知っとるわい、という顔をしつつ、厄介だなあ、と思わざるを得ないが、主成分分析するのに行列は避けて通れない。
前回使用したデータについて、Maximaに計算させてみる。

Maximaへの入力

load(descriptive);
load(lapack);
fpprintprec:6;
X: read_matrix("data2");
[L,W,dummy]: dgeev(cov(X),true,false);
L;
W;
Maximaの出力（上のをbatch()で読み込んだ）
(%i7) L
(%o7) [.330129, .0531125, .00529463]
(%i8) W
[ .714134 .697955 - .0535787 ]
[ ]
(%o8) [ 0.4882 - .551443 - 0.67644 ]
[ ]
[ .501671 - .456912 .734546 ]
固有値（寄与率）は絶対値が一番大きいのが１つ目、二番目に大きいのが２つ目なので、第一主成分の単位ベクトルは(0.714, 0.488, 0.502)、第二主成分の単位ベクトルは(0.698, -0.551, -0.457)である。３つ目の固有値は小さいので、３つ目の固有ベクトルは無視することにする。
今回はたまたま大きい順に並んでいるが、固有値は絶対値の大きさ順に並ぶとは限らないので注意が必要である。
もしdgeev()が使えない場合は、eigens_by_jacobi()を使う。
(%i9) [L,W]:eigens_by_jacobi(cov(X)); L; W;
(%o10) [.330129, .0531125, .00529463]
[ .714134 - .697955 - .0535787 ]
[ ]
(%o11) [ 0.4882 .551443 - 0.67644 ]
[ ]
[ .501671 .456912 .734546 ]
２つ目の固有ベクトルの符号が逆だが、次に求める主成分の大きさの符号が逆になるだけなので、どちらでも良い。

次に、第一主成分、第二主成分を軸に取った時にXの各標本がどういう値になるか（主成分の大きさ）を求める。主成分の大きさYは
Y=XW
なので、

W: submatrix(W,3); /* 弟三主成分を削除 */
Y: X.W;
で求まる。これによって得られるYをグラフにすると、次のようになる。

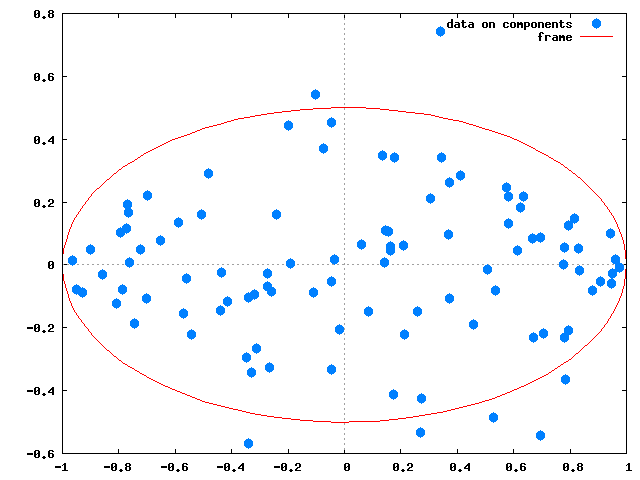
前回のグラフと見比べると、視点が反対（前回のグラフ作成の時はengens_by_jacobi()を使ったため）だが、例えば楕円外の点の分布は大体似ていることがわかる。
これによって、今回使った３次元のデータが、情報の欠落を最小限にして、２次元で分析できる。


特異値分解による方法でもやってみる。
今度はXの中の標本は横に並べる。縦方向の１列が１つの標本である。

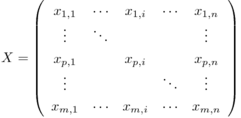
このXが特異値分解によって
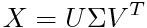
X=U¥Sigma V^T
（Tは転置）と３つの行列（U=左特異行列、Σ=特異値行列、V=右特異行列）の積になる時、Uが主成分の単位ベクトルを縦に並べたもの、Σの対角成分（特異値）が［ｎ×寄与率］の平方根となり、標本の主成分の大きさYは
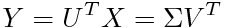
Y=U^TX=¥Sigma V^T
となる。
Maximaで特異値分解するには、LAPACKのdgesvd()を使うと一発である。（LAPACKが使えないと、かなり厳しそうである）

Maximaへの入力

load(lapack);
fpprintprec:6;
X: transpose(read_matrix("data2"));
[s,U,V]: dgesvd(X,true,true)$
U;
s;
Maximaの出力
(%i7) U
[ - .713141 .698967 - 0.053619 ]
[ ]
(%o7) [ - .488765 - 0.55059 - .676727 ]
[ ]
[ - .502532 - .456395 .734279 ]
(%i8) s
(%o8) [5.77344, 2.30564, .727852]
（Vは100x100の行列なので省略）
行列Uに、先程と大体同じ主成分の単位ベクトルがあることと、３つ目の特異値が小さく、寄与率が低いことがわかる。

Maximaへの入力（続き）

S: zeromatrix(2,100); /* 行列Σ(3x100)の上２行分 */
S[1,1]: s[1]; /* 対角成分１ */
S[2,2]: s[2]; /* 対角成分２ */
Y: S.V;
これによって得られるYをグラフにすると、次のようになる。

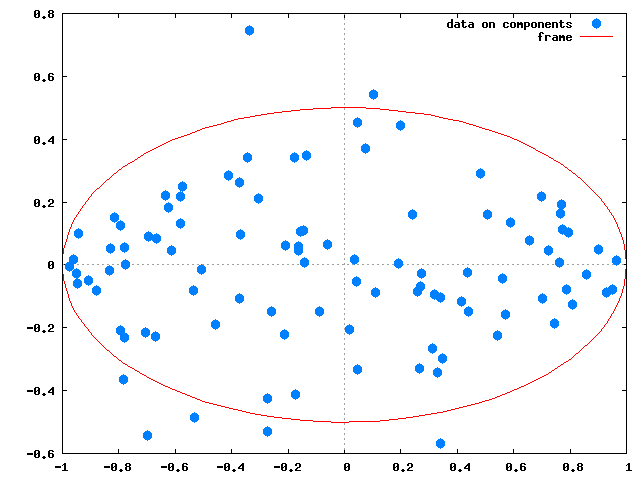
さらに反対向きになったが、そういうものである。


さて、固有ベクトル計算による方法と特異値分解による方法をどう使い分けるかだが、一般に、特異値分解を使う方法の方が計算誤差が少ない、と言われる。固有ベクトル計算による方法だと、共分散行列にする時に一気に情報量が落ちるので、感覚的には納得できるが、使用するモジュールやライブラリの精度による所もあるので、一概には言えないと思う（例えばすごい桁数の共分散行列から固有ベクトルを求めれば精度は上がるはず）。

また、ライブラリの特性の問題かも知れないが、eigens_by_jacobi()やLAPACKのdgeev()では固有ベクトルが固有値の絶対値の順に並ぶとは限らないので、運が悪いと固有値を見て固有ベクトルを並び替える必要が生じる。それに対し、LAPACKのdgesvd()は特異値が必ず大きい方から並ぶので、LAPACKを使うなら特異値分解による方法の方が楽かも知れない。

上の例にも固有ベクトル計算による方法と特異値分解による方法とで計算結果に若干誤差があるが、どちらが正確なのかを少し調べてみる。
Yeを固有ベクトルによる計算結果、Ysを特異値分解による計算結果として、Maximaにて

transpose(Ye).Ye;
transpose(Ys).Ys;
とやってみると
[ 33.3325378 - .03917623549 ]
(%o) [ ]
[ - .03917623549 5.316048774 ]

[ 33.33259721 - 1.5447767401e-6 ]
(%o) [ ]
[ - 1.5447767401e-6 5.315997826 ]

と出てくる。特異値分解による結果の方が第一主成分の２乗和が大きく、共分散が0に近いので、今回は（も？）特異値分解による方法の方が正確だったと考えられる。


上に書いた以外の、今回使ったMaximaへの入力を記録する。
グラフ作成用

write_data(transpose(Y), "data_tmp"); /* 行列からリストへの変換 */
A: read_nested_list("data_tmp");
plot2d([[discrete,A],[parametric,cos(t),sin(t)/2,[t,0,2*%pi]]],[style,points,lines],[legend,"data on components","frame"],[gnuplot_term,png],[gnuplot_out_file,"data2onc.png"],[nticks,100]);
dgesvdの動作理解用
load(lapack);
X:matrix([1,2],[2,3],[-3,-5]);
[s,U,V]: dgesvd(X,true,true);
S: apply(diag_matrix,s);
S: addrow(S,[0,0]);
U.S.V;
主成分分析の計算結果比較用
load(descriptive);
load(lapack);
X:matrix([1,2],[2,3],[-3,-5]);
[L1,W1]:eigens_by_jacobi(cov(X));
[L2,W2,dummy]:dgeev(cov(X),true,true);
W1: matrix([0,1],[1,0]).W1 /* or columnswap() */;
W2: matrix([0,1],[1,0]).W2;

[s,U,V]: dgesvd(transpose(X),true,true);
S: apply(diag_matrix,s);
V: submatrix(3,V); /* remove 3rd row */

Y1: transpose(W).transpose(X); /* eigens_by_jacobi */
Y2: transpose(W).transpose(X); /* dgeev */
Y3: S.V; /* dgesvd */
Y4: transpose(U).transpose(X); /* eigenvector by dgesvd */