統計学復習メモ18: 少数のベルヌーイ試行による発生確率の区間推定

問：ある機械が20個の部品を作ったら、不良品が2個出てきた。この機械が1個作る毎に不良品を発生させる確率は一定だとすると、不良品発生率は信頼度95%の信頼区間として何%〜何%の間と推測できるか。

観測誤差を考えなければ、すなわち点推定量としては、推定確率はもちろん2/20=0.1である。しかし、標本はたった20個である。これをもって、だから2000個作ったら200個の不良品が出ることが予想される、と言うのはあまりにも乱暴だし、直感的にナンセンスであろう。サンプルが少なすぎて信憑性が低く、説得力が無いのである。
信頼性を高めるにはサンプル数を増やせば良いが、例えば以前のエントリーに書いたような計算方法では、推定確率が0.1前後の場合に誤差を±0.05以内にするには、(1.96/0.05)2*0.1*0.9＝約140個のサンプルが必要になる。サンプル数を先に決められない場合や、サンプルはそれしかないという場合は、推定発生率はこの範囲に入る、という信頼区間を求めるしか無い。

観測されたベルヌーイ試行の成功回数（発生回数）からの元の成功率（発生率）の区間推定については、以前のエントリーに書いたように信頼区間の公式がある。
I \in \hat{p}\pm Z\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} ...(1)
（p^は点推定量、Zは標準正規分布N(0,1)に従う値、nはベルヌーイ試行の標本数）

従って、p^=0.1、Z=1.96（右側2.5%点）、n=20とすると、95%信頼区間は0.1±1.96√0.0045 = 0.1±0.131、すなわち-3.1%〜23.1である。（完）

イエース、公式一発、ビバ統計学！
...ちょっと待て、確率なのにマイナスの値？何を間違えたのだろう？

発生率が一定で、１回の試行の結果は発生するかしないかの２通りしか無い試行（ベルヌーイ試行）を複数回行った時の発生回数は二項分布に従う。そして試行回数が十分大きければ二項分布は正規分布で近似できる。試行回数をn、発生率をpとすると、発生回数は平均np、分散np(1-p)の正規分布に（近似的に）従う。観測される発生率（推定確率）は発生回数を試行回数で割ったものだから、平均p、分散p(1-p)/nの正規分布に（近似的に）従う。母分散が既知の場合、正規分布に従う標本の推定値は毋分散÷標本数を分散とする正規分布に従うとするのが区間推定の定跡である（母分散が未知の時は標本分散を使うのでｔ分布に従うとする）から、信頼区間Iは
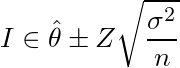
I \in \hat{\theta}\pm Z\sqrt{\frac{\sigma^2}{n}}
（θ^は点推定量、Zは標準正規分布のZ値、このnは正規分布に従う標本の数なので今回は1）
で与えられる。冒頭の問題については、θ^=p、σ2=p(1-p)/nなので、信頼区間はやはり(1)の公式の通りである。

という訳で、二項分布を正規分布に近似しているのが問題のようである。
次のグラフは、n=20として、p=0.5とp=0.1の二項分布とN(np, p(1-p)/n)の正規分布を比較したものである。

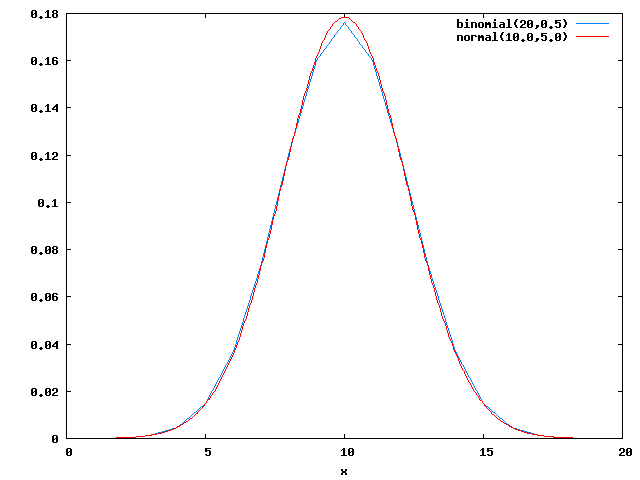
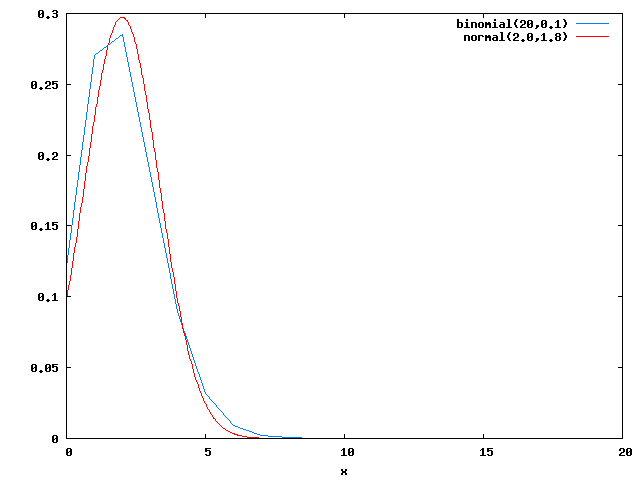
青線が二項分布、赤線が正規分布である。p=0.5だとかなり近いが、p=0.1だと差がある。比率が0.5から遠いほど、二項分布の正規分布への近似は悪くなるのである。
大体、正規分布に近似するということは0より小さい確率や1より大きい確率を認めるということであり、n=20でp=0.1の場合、正規分布の左側6.8%は負の値に入り、無効になってしまうのである。この6.8%を全てp=0の所に加算すれば（信頼区間の下限が負の値なら0に補正すれば）いいだけの話とも言えなくはないが、pの推定値が0に近づくと急激にp=0の確率が上昇することになるので、ちょっと強引であろう。

上記の比率の信頼区間の公式(1)は、np<5またはn(1-p)<5の場合は不適、すなわちベルヌーイ試行の成功回数（発生回数）も失敗回数（発生しなかった回数）も5以上でないと使えないと言われているらしい。視聴率調査や投票率予想なら最低5人が観て／投票していないと、この公式を使うのは適当でないのである。それに基づくと、冒頭の問題もnp=2なのでこの公式は使えない。

ではこの場合はどのようにして信頼区間を求めれば良いのだろうか。それを解決してくれるのがClopper-Pearson methodによる通称Exact Confidence Interval(Exact CI)である。
区間推定の原点に立ち返ると、信頼区間とは、ある推定値がある信頼度で収まる値の範囲であり、まともに計算するなら事前確率、事後確率を考慮して計算すべきものであるが、それに代えて、推定の元になった観測値及びそれより稀な値が発生する確率が（1-信頼度）以下であるような推定値の範囲を信頼区間として計算する、というのを二項分布のパラメーター推定について行うのがClopper-Pearson methodである。冒頭の問題なら、95%の確率でpが0.1の前後のどこまでの範囲に含まれるかを求める代わりに、pが0.1よりどこまで小さければ不良品が2個以上出る確率が2.5%になるか、pが0.1よりどこまで大きければ不良品が2個以下である確率が2.5%になるか、を求めるのである。
という訳で、ベルヌーイ試行の確率の推定値の信頼区間の下限Plbと上限Pubを束縛する式は次のようになる。（αは1-信頼度）
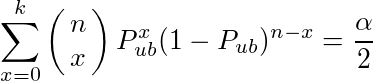
\sum_{x=0}^{k}\pmatrix{n \cr x}P_{ub}^x (1-P_{ub})^{n-x}=\frac{\alpha}{2}

\sum_{x=k}^{n}\pmatrix{n \cr x}P_{lb}^x (1-P_{lb})^{n-x}=\frac{\alpha}{2}
これを計算したものがExact CIで、BetaCDF(x,a,b)をベータ分布の累積密度関数として、その逆関数を用いて、
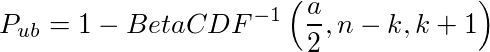
P_{ub}=1-BetaCDF^{-1}\left(\frac{a}{2},n-k,k+1\right)
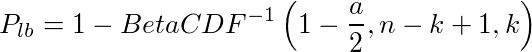
P_{lb}=1-BetaCDF^{-1}\left(1-\frac{a}{2},n-k+1,k\right)
と書けるらしい。

Maximaにはベータ分布の累積密度関数の逆関数（β値を求める関数）がquantile_beta()という名前で存在するので、これを使って信頼区間の上限を計算できる。
(%i1) load(distrib);
(%i2) Pub(n,k,a) := 1-quantile_beta(a/2, n-k, k+1);
(%i3) Plb(n,k,a) := 1-quantile_beta(1-a/2, n-k+1, k);
(%i4) Pub(20,2,0.05);
(%o4) 0.317
(%i5) Plb(20,2,0.05);
(%o5) .012349

答：1.23%から31.7%の間

参考文献：Understanding Binomial Confidence Intervals

この計算方法によって、20回の試行で発生した回数が何回なら、推定発生率の信頼水準95%の下限と上限がどうなるかを表にしてみる。（発生回数＝0, 20については片側5%を除いたもの、それ以外は両側2.5%ずつを除いたもの）
発生回数発生率下限点推定値発生率上限
0000.1391
10.0012650.050.2487
20.012350.10.317
30.032070.150.3789
40.057330.20.4366
50.086570.250.491
60.11890.30.5428
70.15390.350.5922
80.19120.40.6395
90.23060.450.6847
100.2720.50.728
110.31530.550.7694
120.36050.60.8088
130.40780.650.8461
140.45720.70.8811
150.5090.750.9134
160.56340.80.9427
170.62110.850.9679
180.6830.90.9877
190.75130.950.9987
200.860911
10回の試行の場合は次のようになる。（発生回数＝0, 10は片側5%を除いたもの）
発生回数発生率下限点推定値発生率上限
0000.2589
10.0025290.10.445
20.025210.20.5561
30.066740.30.6525
40.12160.40.7376
50.18710.50.8129
60.26240.60.8784
70.34750.70.9333
80.44390.80.9748
90.5550.90.9975
100.741111


n=20の時に信頼水準95%のExact CIと正規分布近似CIとがどれくらいずれているかを、グラフで見てみる。

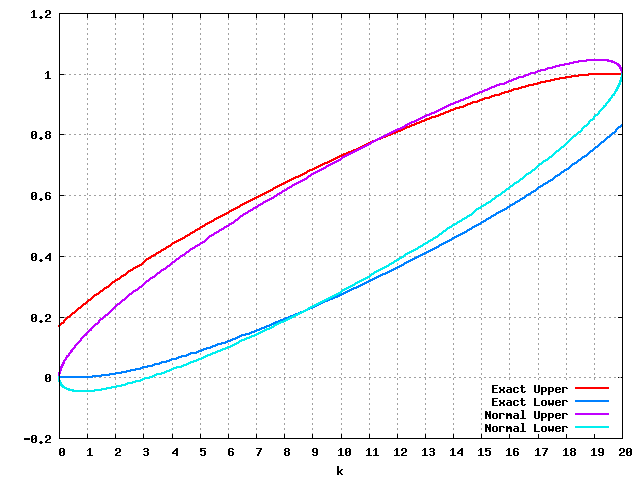
発生回数が4回以下、16回以上だとかなりずれていることがわかる。


Exact CIの上限と下限は、ベータ分布とF分布の関係から、次のようにF分布を用いて書かれることが多いようである。
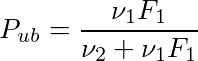
P_{ub}=\frac{\nu_1F_1}{\nu_2+\nu_1F_1}
但し、ν1=2(k+1)、ν2=2(n-k)、F1は自由度ν1,ν2のF分布の(1-α/2)点（右側がα/2点となるF値）
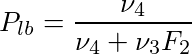
P_{lb}=\frac{\nu_4}{\nu_4+\nu_3F_2}
但し、ν3=2(n-k+1)、ν4=2k、F2は自由度ν3,ν4のF分布の(1-α/2)点（右側がα/2点となるF値）

参考リンク（いずれもPDF）：
http://www.nfri.affrc.go.jp/yakudachi/sampling/pdf/Clopper.pdf
Confidence Intervals for a Binomial Proportion

これもMaximaで使ってみる。
(%i1) load(distrib);
(%i2) Pub(n,k,a) := block([v1,v2,F1],
v1: 2*(k+1),
v2: 2*(n-k),
F1: quantile_f(1-a/2, v1, v2),
v1*F1/(v2+v1*F1)
);
(%i3) Plb(n,k,a) := block([v3,v4,F2],
v3: 2*(n-k+1),
v4: 2*k,
F2: quantile_f(1-a/2, v3, v4),
v4/(v4+v3*F2)
);
(%i4) Pub(20,2,0.05);
(%o4) 0.317
(%i5) Plb(20,2,0.05);
(%o5) .012349

同じ結果が得られたが、幾分面倒である。Maximaのように、ベータ分布のβ値を求める機能が使えるなら、ベータ分布の式を使う方がずっとシンプルである。


このClopper-Pearson method、確率／統計の原始的な問題に関係してて、基本的でニーズが高いはずのノウハウだと思うのだが、気のせいだろうか？
20個中2個あれば全体の確率は大体0.1だろうと推測することに、これだけ誤差があるのである。
筆者は最初に工学系の学部で統計学に触れてから15年以上経つが、Clopper-Pearsonという名前もこういう標本比率の誤差範囲の問題があるのも、これまで寡聞にして聞いたことが無かった。統計学をかじった人には当たり前すぎて、しかし統計学に無縁の人には関心を持たれない、落とし穴なのでは無いだろうか。
何と言うか、正しい知識を持って臨めば真理を衝いているにもかかわらず、誤解により統計学の様々な公式が様々な結果を生み出すによって、統計学が怪しい学問、人を騙すため、煙に巻く為の学問と思われているような気がしてしまう。


●上記以外の、今回使ったMaximaの入出力
正規分布近似による信頼区間の計算
(%i1) p:0.1;
n:20;
p-quantile_normal(0.975,0,1)*sqrt(p*(1-p)/n);
p+quantile_normal(0.975,0,1)*sqrt(p*(1-p)/n);
(%o3) -.03148
(%o4) .2315
二項分布と正規分布の比較のグラフ作成用
p:0.5;
xx: makelist(x,x,0,20)$
yy: makelist(binomial(20,x)*p^x*(1-p)^(20-x),x,0,20)$
plot2d([[discrete,xx,yy],pdf_normal(x,20*p,sqrt(20*p*(1-p)))], [x,0,20],
[legend,binomial(20, p),normal(20*p, 20*p*(1-p))],
[gnuplot_term,png],[gnuplot_out_file,"~/exactci01.png"])$
二項分布の正規分布近似で発生率が負の値に入る確率
(%i1) cdf_normal(0,2,sqrt(1.8)), numer;
(%o1) .06802
Exact CIと正規分布近似CIの比較のグラフ作成用
Plb0(n,k,a) := k/n - quantile_normal(1-a/2,0,1)*sqrt((k/n)*(1-k/n)/n);
Pub0(n,k,a) := k/n + quantile_normal(1-a/2,0,1)*sqrt((k/n)*(1-k/n)/n);
plot2d([Pub(20,k,0.05),Plb(20,k,0.05),Pub0(20,k,0.05),Plb0(20,k,0.05)],[k,0,20],
[legend,"Exact Upper","Exact Lower","Normal Upper","Normal Lower"],
[style,[lines,2,2],[lines,2,1],[lines,2,3],[lines,2,7]],
[gnuplot_preamble, "set key bottom; set grid; set xtics 1"]);