「統計学が最強の学問である［数学編］」のロジスティック回帰をやってみた

何年も前に買って読んでいなかった「統計学が最強の学問である」シリーズを、今更ながら読んでいる。その［数学編］はほとんど知っている内容だったので、半分くらいは流し読みしたのだが、所々、特に微分・積分以降はわかっているようでわかっていなかったことを思い知らされて勉強になったし、大変面白かった。

さて、p.490のロジスティック回帰の最急降下法の説明の所に、「気になる方はエクセルや何らかのプログラミング言語を使って挑戦していただければと思いますが、...」と書かれている。気にならない訳がないので、やってみた。

問題は、次のようなデータについて、トラブルの有無がどの程度リピート率に影響するかをロジスティック回帰分析で調べるというものである。

利用時間	トラブル	リピート	人数
ランチ	なし	なし	207
ランチ	なし	あり	23
ランチ	あり	なし	18
ランチ	あり	あり	2
ディナー	なし	なし	435
ディナー	なし	あり	290
ディナー	あり	なし	15
ディナー	あり	あり	10

●コード

import numpy as np

# 元データ(p.483)
data = np.array([
    # ディナーダミー、トラブルダミー、リピートダミー、人数
    [0, 0, 0, 207],
    [0, 0, 1, 23],
    [0, 1, 0, 18],
    [0, 1, 1, 2],
    [1, 0, 0, 435],
    [1, 0, 1, 290],
    [1, 1, 0, 15],
    [1, 1, 1, 10]])

# 各行を人数分に展開したもの
data_flat = np.repeat(data[:, :3], data[:, 3], axis=0)

X = data_flat[:, :2] # ディナーダミー、トラブルダミー
X = np.hstack((np.ones_like(X[:,:1]), X)) # 1列目に全て1の列を追加
y = data_flat[:, 2]  # リピートダミー

# コスト関数 C(β) = -log L(β) = - \sum { (y - 1) x^T β - log(1 + exp(-x^T β)) }
# L(β) = \Pi p^y (1-p)^(1-y), p = 1 / (1 + exp(-x^T β))
def cost_function(X, y, beta):
    return -np.sum((y - 1) * (X @ beta) - np.log(1 + np.exp(-X @ beta)))

# 勾配 ∂C/∂β のテスト(p.490)
beta = np.array([1.0, 1.0, 1.0])
delta = 0.0001
gradient = [
    (cost_function(X, y, beta + [delta, 0, 0]) - cost_function(X, y, beta)) / delta,
    (cost_function(X, y, beta + [0, delta, 0]) - cost_function(X, y, beta)) / delta,
    (cost_function(X, y, beta + [0, 0, delta]) - cost_function(X, y, beta)) / delta,
]

print("first gradient =", gradient)

# 勾配が最小になるβを求める
# βから勾配に学習率を掛けたものを引くのを繰り返す
learning_rate = 0.005

for i in range(120):
    gradient = np.array([
        (cost_function(X, y, beta + [delta, 0, 0]) - cost_function(X, y, beta)) / delta,
        (cost_function(X, y, beta + [0, delta, 0]) - cost_function(X, y, beta)) / delta,
        (cost_function(X, y, beta + [0, 0, delta]) - cost_function(X, y, beta)) / delta,
    ])
    beta -= learning_rate * gradient

print("beta =", beta)

# オッズ比(p.492)
print("odds of beta1, beta2 =", np.exp(beta[1:]))

# scikit-learnのLogisticRegressionで検算する
from sklearn.linear_model import LogisticRegression

X = data_flat[:, :2] # ディナーダミー、トラブルダミー
y = data_flat[:, 2]  # リピートダミー

lr = LogisticRegression().fit(X, y)
print("sklearn beta0 =", lr.intercept_, ", (beta1, beta2) =", lr.coef_[0])
print("sklearn odds of beta1, beta2 =", np.exp(lr.coef_[0]))

●実行結果

first gradient = [523.157877723861, 362.3960970844564, 29.430456188492826] beta = [-2.19686992 1.79119201 0.00347654] odds of beta1, beta2 = [5.99659623 1.00348259] sklearn beta0 = [-2.12298445] , (beta1, beta2) = [ 1.70835681 -0.00918478] sklearn odds of beta1, beta2 = [5.51988382 0.99085727]

betaの1つ目が切片、2つ目と3つ目が回帰係数で、それぞれ小数点第2位を四捨五入すると[-2.2, 1.8, 0.0]、回帰係数をオッズ比にすると[6.0, 1.0]である。p.493の結果と一致した。トラブル有無のオッズ比が1.0なので、リピート率への影響は無しという結果である。
検算の為にscikit-learnのLogisticRegressionでもやってみたら、切片が-2.1、回帰係数の1つ目が1.7と少し違う結果になり、LogisticRegressionのハイパーバラメーターを色々変えてみても本の記載と同じ結果にはできなかった。そういうものなのだろうか。コスト関数の勾配は本の結果の方が小さかったので、本の結果の方が良いと思われる。

さらに読み進めると、別の例について計算過程抜きで、ロジスティック回帰の結果が出てきた。 p.531より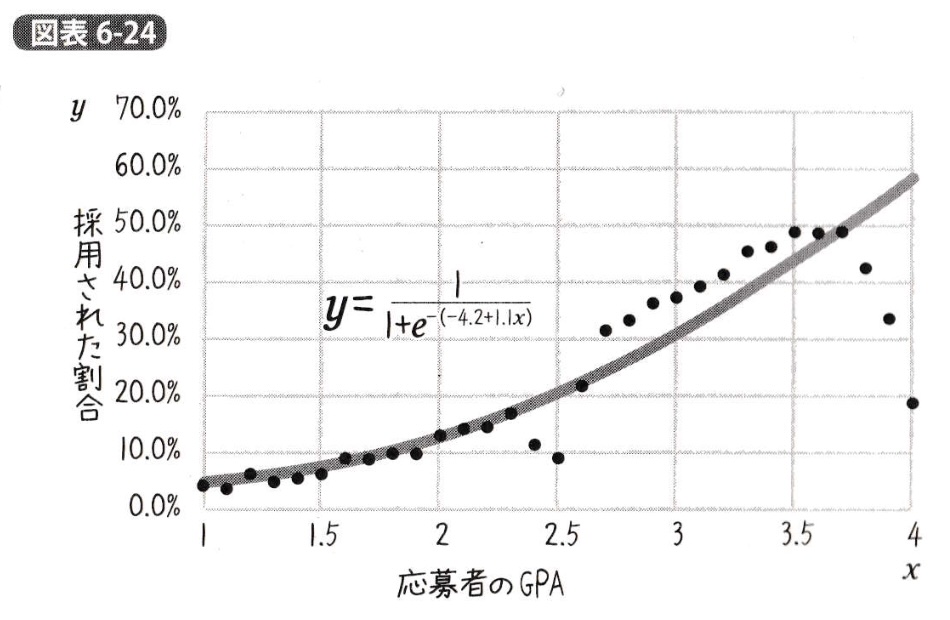：気にならない訳がないので、ついでに同じやり方でやってみた。

●コード

import numpy as np
import matplotlib.pyplot as plt

# 元データ(p.497)
data_x = np.arange(1.0, 4.1, 0.1)
data_y = np.array([4, 3.5, 6, 5, 5.5, 6, 9, 9, 10, 10,
     13, 14, 14, 17, 11.5, 9, 21.5, 31.5, 33.5, 36.5,
     37.5, 39.5, 41.5, 45.5, 46.5, 49, 49, 49, 42.5, 33.5, 18.5]) / 100

# 各xの人数の分布は平均2.5、分散1の正規分布に従うとする
n = np.repeat(1000 / np.sqrt(2 * np.pi) * np.exp(- (data_x - 2.5) ** 2 / 2), 2)
n[0::2] *= data_y        # 合格者数
n[1::2] *= (1 - data_y)  # 不合格者数
n = n.astype(int)

# 前のコードと同じ形式のdata
data = np.array([
    np.repeat(data_x, 2),
    [1, 0] * len(data_x)]  # 合格=1、不合格=0
).T

# 各行を人数分に展開したもの
data_flat = np.repeat(data, n, axis=0)

# ロジスティック回帰
X = data_flat[:, :1]
X = np.hstack((np.ones_like(X[:,:1]), X)) # 1列目に全て1の列を追加
y = data_flat[:, 1]

beta = np.array([1.0, 1.0])

def cost_function(X, y, beta):
    return -np.sum((y - 1) * (X @ beta) - np.log(1 + np.exp(-X @ beta)))

learning_rate = 0.0001
delta = 0.0001

for i in range(1000):
    gradient = np.array([
        (cost_function(X, y, beta + [delta, 0]) - cost_function(X, y, beta)) / delta,
        (cost_function(X, y, beta + [0, delta]) - cost_function(X, y, beta)) / delta,
    ])
    beta -= learning_rate * gradient

print("beta =", beta)

# 結果のグラフ表示(p.531)
plt.figure(figsize=(8, 4))
plt.scatter(data_x, data_y, c='k')

plt.plot(data_x, 1 / (1 + np.exp(-(beta[0] + beta[1] * data_x))), c='k', alpha=0.5, lw=5)

plt.grid()
plt.xlim(1, 4)
plt.ylim(0, 0.7)
plt.show()

# scikit-learnのLogisticRegressionで検算する
from sklearn.linear_model import LogisticRegression

X = data_flat[:, :1]
y = data_flat[:, 1]

lr = LogisticRegression().fit(X, y)
print("sklearn beta0 =", lr.intercept_, ", beta1 =", lr.coef_[0])

●実行結果

beta = [-4.1350283 1.1067759] sklearn beta0 = [-4.12820171] , beta1 = [1.10448998]

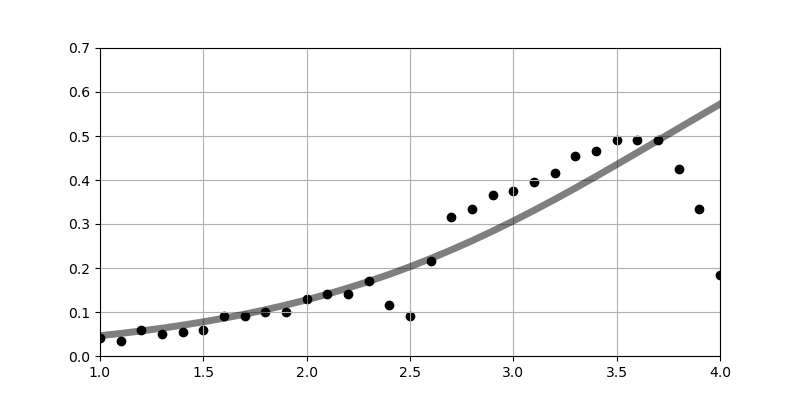
データは、スキャナーでスキャンしたグラフに罫線を重ねて、目視で大まかに読み取った。
応募者の人数の分布は書かれていないので不明である。xの1〜4まで全て同じ人数とするとまあまあ違う結果（β=[-3.8, 0.98]）になったが、試しに人数の分布を正規分布としてやってみると、本に記載のグラフと近い結果（β=[-4.1, 1.1]）になった。

Weblog on mebius.tokaichiba.jp

「統計学が最強の学問である［数学編］」のロジスティック回帰をやってみた

コメント