中心極限定理の証明の理解でつまずいた

2年前に統計検定準1級の勉強をしていた時、どこかで特性関数を用いた中心極限定理の証明を読んで、なるほど、と思ってノートに書き残した。
先週、そのノートを読んだら、理解できない部分があって、結構な時間悩んでしまった。
同じように悩む人はあまり居ないと思うが、自分用にメモしておく。

中心極限定理とは、期待値がμ、分散がσ2である任意の独立同一分布(i.i.d)に従うn個の確率変数Xiの平均が、その分布がどういう形状であっても、nを大きくすると近似的に期待値μ、分散σ2/nの正規分布に従うというものである。

中心極限定理
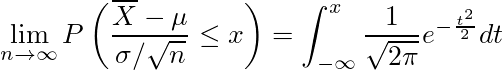
\lim_{n \to \infty} P\left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \le x \right) = \int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}} dt

証明方法としては、特性関数の連続定理により、ある確率変数Xnの特性関数φn(t)がn→∞とすると全てのtでXの特性関数φ(t)一致するなら、XnはXに分布収束するというのを使う。
つまり、Xiの平均を平均μ、分散σ2/nで標準化したZnの特性関数φZn(t)が、標準正規分布の特性関数φZ(t)に一致することを示せば良い。

標準正規分布に従うZの特性関数は
\begin{align}<br /> \phi_Z(t) & = E[e^{itZ}] = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{z^2}{2}} e^{itz} dz \\<br /> &= \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-\frac{1}{2}((z-it)^2 + t^2)} dz \\<br /> &= \frac{1}{\sqrt{2\pi}} e^{-\frac{t^2}{2}} \int_{-\infty}^{\infty} e^{-\frac{(z-it)^2}{2}} dz \\<br /> &= e^{-\frac{t^2}{2}}<br /> \end{align}
である。最後は
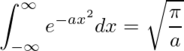
\int_{-\infty}^{\infty} e^{-a x^2} dx = \sqrt{\frac{\pi}{a}}
であることを用いた。

本題の、Znの特性関数を計算する。
\begin{align}<br /> \phi_{Z_n}(t) & = E[e^{itZ_n}] = E\left[\exp \left( it\frac{\sqrt{n}}{\sigma}\frac{1}{n}\sum_{j=1}^n (X_j-\mu) \right)\right] \\<br /> &= E\left[\prod_{j=1}^n \exp\left(it\frac{(X_j-\mu)}{\sqrt{n} \sigma} \right)\right] \\<br /> &= \left( E\left[ \exp\left(it\frac{(X_1-\mu)}{\sqrt{n} \sigma} \right)\right] \right)^n \\<br /> \end{align}

今回、この最後の変形が何故成り立つのかがわからず、調べまくってしまった。結局、九州大学の原先生の公開講座資料の第26頁の「最後のところでは，Xi の分布が同分布であることを用いました」を見て、Xiがi.i.dであることを思い出して解決した。
上の数式では敢えてX1と書いた（原先生の資料でもそのようになっている）が、筆者のノートでは（おそらくその元資料でも）この部分がXと書かれていたのが、筆者にとって混乱の元だった。

計算を続ける。マクローリン展開により、
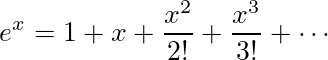
e^x = 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots
なので、2乗の項までを展開して、
\begin{align}<br /> \phi_{Z_n}(t) & = \left( E\left[1 + \frac{it}{\sqrt{n}}\left(\frac{X_1-\mu}{ \sigma}\right) - \frac{t^2}{2n}\left(\frac{X_1-\mu}{ \sigma}\right)^2 - O(\frac{1}{n\sqrt{n}}) \right]\right)^n \\<br /> &= \left(1 - \frac{t^2}{2n} - O(\frac{1}{n\sqrt{n}}) \right)^n<br /> \end{align}
と変形できる。O(f(n))は「ランダウの記号」というもので、nを大きくした時に高々f(n)の定数倍となることを表す。3乗の項以降はnを大きくした時に0に収束するので、このように省略している。

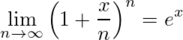
\lim_{n\to\infty} \left(1 + \frac{x}{n} \right)^n = e^x
なので、
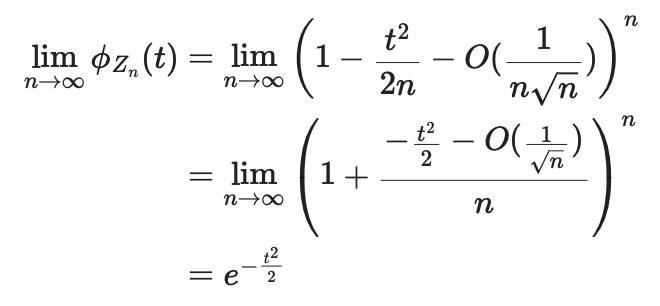
\begin{align}<br /> \lim_{n\to\infty} \phi_{Z_n}(t) & = \lim_{n\to\infty} \left(1 - \frac{t^2}{2n} - O(\frac{1}{n\sqrt{n}}) \right)^n \\<br /> &= \lim_{n\to\infty} \left(1 + \frac{- \frac{t^2}{2} - O(\frac{1}{\sqrt{n}})}{n} \right)^n \\<br /> &= e^{- \frac{t^2}{2}}<br /> \end{align}
となり、標準正規分布と特性関数が一致するので、Znは標準正規分布に収束する。

ついでに上述の原先生の資料で、特性関数がフーリエ変換と同じであることに初めて気付かされて驚いた。色々勉強になった。