F分布は分母の自由度が大きいとχ2分布に近似できる？

「統計検定 ２級 公式問題集 2017～2019年」の解説部分のコメントの中に、

自由度(5,77)のF分布の上側1%点は付表には与えられていないため、近似的に考える。すなわち、残差の自由度77が十分大きいので、F統計量に5を掛けた統計量の分布が自由度5のカイ二乗分布で近似できると考えてよい。
というのがある（残差というのは分散分析の文脈のもので、分母のこと）。最初にこれを読んだ時は理解できた気がして、試験前の復習の為にメモっておいたのだが、試験後にメモ書きを捨てる前にメモを1つ1つ読んでると、このことだけ理解できなかった。

確かに、同書のα=0.05のF分布表の一番下の行（分母の自由度が一番大きい所）とカイ二乗分布表のα=0.05の列を比較すると、F分布表の数値に分子の自由度を掛けた値がカイ二乗分布表の値と大体一致するし、別の本の自由度が∞の行があるF分布表の∞の行と同様に比較すると完全に一致している。

自由度(5,100)のF分布のFを5倍した確率密度と自由度5のχ2分布の確率密度のグラフを比較しても、確かにほぼ一致している。自由度(5,10)のものなどと比較すると、分母の自由度が大きいほどχ2分布に近づくことが見て取れる。

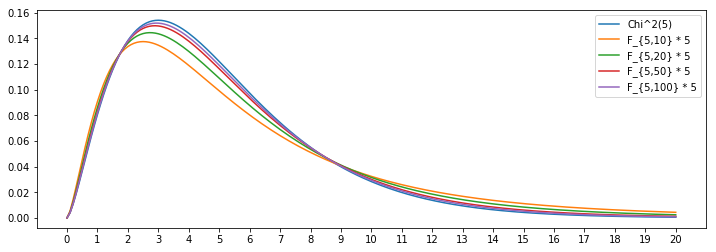
しかし、自由度(m,n)のF分布に従うFは、X,Yがそれぞれ独立で自由度m,nのχ2分布に従うとすると
F = \frac{X / m}{Y / n}
であり、例えばn=100のχ2分布の確率密度は

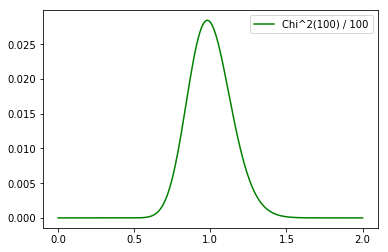
なので、Yの期待値は1であるがY=1ではないと思った。

自由度mのχ2分布の確率密度関数は
f(x) = \frac{1}{\Gamma(\frac{m}{2})2^{\frac{m}{2}}} x^{\frac{m}{2}-1} e^{-\frac{x}{2}}
で、自由度(m,n)のF分布の確率密度関数は
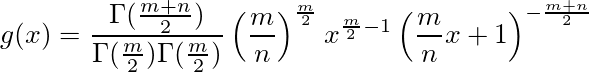
g(x) = \frac{\Gamma(\frac{m+n}{2})}{\Gamma(\frac{m}{2})\Gamma(\frac{m}{2})} \left(\frac{m}{n}\right)^\frac{m}{2} x^{\frac{m}{2}-1} \left(\frac{m}{n}x+1\right)^{-\frac{m+n}{2}}
だそうなので、n→∞の時にこれらが一致することを確認するしかないか...と思ったが、ネットで調べてみると、大体
\lim_{n\to\infty} Y/n = 1
で片付けられていた。

もう少し丁寧な説明だと、それぞれ独立の、自由度1のカイ二乗分布に従うYiを使って
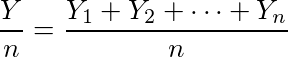
\frac{Y}{n} = \frac{Y_1 + Y_2 + \cdots + Y_n}{n}
とすると、大数の法則（大数の強法則）より
\lim_{n\to\infty} \frac{Y}{n} = E[Y_1] = 1
なので
\lim_{n\to\infty} mF = \lim_{n\to\infty} \frac{X}{Y/n} = X
とのことである。

何でn=77くらいでmFが十分にχ2分布に近似できると言えるんだろう、とかすっきりしない所はあるが、まあ実際そうなのだからそういうものだと覚えておくしかないだろうか。

●グラフ描画に用いたコード 
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2, f
plt.figure(figsize=(12,4))
plt.plot(chi2.pdf(np.linspace(0, 20, 201), 5), label="Chi^2(5)")
for df in [10, 20, 50, 100]:
    plt.plot(f.pdf(np.linspace(0, 20, 201) / 5, 5, df) / 5, label="F_{5,%d} * 5" % df)
plt.xticks(np.linspace(0, 200, 21), np.linspace(0, 20, 21).astype('int'))
plt.legend()
plt.show()

plt.plot(chi2.pdf(np.linspace(0, 200, 201), 100), color='g', label="Chi^2(100) / 100")
plt.xticks(np.linspace(0, 200, 5), np.linspace(0, 2.0, 5))
plt.legend()
plt.show()