Wekaでベイジアンネットワークの事後確率を計算

ベイジアンネットワークの復習をしていて、確率的グラフィカルモデル‐ベイジアンネットワークとその周辺‐（オペレーションズ・リサーチ 2013年4月号）という記事を見つけた。その中に、Family Out Problemという有名な例題（下図）の紹介があり、p.194に、

表1~3で与えられたCPTの値と式(11)を利用して丹念に計算することにより P(X₁=1|X₃=1,X₅=1)=0.7577···という結論を得る.

と書かれていたので、これを自力で計算できたらベイジアンネットワークを理解できたことにしよう、と思って、丹念に計算してみたら、その値にならなかった。

Family Out Problem

ここでは、
X₁: Family Out
X₂: Bowel Problem
X₃: Light On
X₄: Dog Out
X₅: Hear Bark
（それぞれ2値の確率変数）であり、それぞれの条件付き確率は次の通りである。
P(X₁=1) = 0.15
P(X₂=1) = 0.01
P(X₃=1 | X₁=0) = 0.05
P(X₃=1 | X₁=1) = 0.6
P(X₄=1 | X₁=0, X₂=0) = 0.3
P(X₄=1 | X₁=0, X₂=1) = 0.97
P(X₄=1 | X₁=1, X₂=0) = 0.9
P(X₄=1 | X₁=1, X₂=1) = 0.99
P(X₅=1 | X₄=0) = 0.01
P(X₅=1 | X₄=1) = 0.7

$P(X_1=1 | X_3=1, X_5=1) = \frac{\sum_{X_2}\sum_{X_4} P(X_1=1, X_2, X_3=1, X_4, X_5=1)}{\sum_{X_1}\sum_{X_2}\sum_{X_4} P(X_1, X_2, X_3=1, X_4, X_5=1)}$
なので、Pythonで

P00101 = 0.85 * 0.99 * 0.05 * 0.7 * 0.01
P00111 = 0.85 * 0.99 * 0.05 * 0.3 * 0.7
P01101 = 0.85 * 0.01 * 0.05 * 0.03 * 0.01
P01111 = 0.85 * 0.01 * 0.05 * 0.97 * 0.7
P10101 = 0.15 * 0.99 * 0.6 * 0.1 * 0.01
P10111 = 0.15 * 0.99 * 0.6 * 0.9 * 0.7
P11101 = 0.15 * 0.01 * 0.6 * 0.01 * 0.01
P11111 = 0.15 * 0.01 * 0.6 * 0.99 * 0.7

P35 = P00101 + P00111 + P01101 + P01111 + P10101 + P10111 + P11101 + P11111
P135 = P10101 + P10111 + P11101 + P11111
P1_35 = P135 / P35
print(P1_35)

とすると、0.8578...という数値になった。どこか読み間違えたかと思って、

def prob(x1, x2, x3, x4, x5):
    p = 1.0
    p *= (0.85, 0.15)[x1]
    p *= (0.99, 0.01)[x2]
    p *= ((0.95, 0.05), (0.4, 0.6))[x1][x3]
    p *= (((0.7, 0.3), (0.03, 0.97)), ((0.1, 0.9), (0.01, 0.99)))[x1][x2][x4]
    p *= ((0.99, 0.01), (0.3, 0.7))[x4][x5]
    return p

P135 = sum([prob(1, x2, 1, x4, 1)
             for x2 in range(2)
             for x4 in range(2)])
P35 =  sum([prob(x1, x2, 1, x4, 1)
             for x1 in range(2)
             for x2 in range(2)
             for x4 in range(2)])
P1_35 = P135 / P35
print(P1_35)

と書いてみたが、やはり0.8578...だった。

上記の記事内の条件付き確率表に誤記があり、0.7577...というのは元の確率表で計算された値か、とも思ったが、どの文書のFamily Out Problemを見ても確率は同じだった。

正解は何なのか、何らかのツールで確認しようと思って、Pythonのベイジアンネットワーク関連のツールを探したが、適当なものがなかなか見つからなかった。

scikit-learnには"Naive Bayes"のAPIはあるがベイジアンネットワークは見つからない。
PyMCやBayesPyは、きっとうまく使えばこの計算ができるのだろうが、ネットワークを定義して、CPT（conditional probability table、条件付き確率表)とevidence（観測値）を与えて事後確率を計算する直接的なサンプルコードが見つからなかったので、諦めた。
PBNTにはそういうサンプルコードがあったので、使ってみたが、P(X₁=1|X₃=1,X₅=1)=0.2018...という全然違う値が出力された。P(X₅=1)=0.2831と、これは正しい値が出たので、ネットワークとCPTは合ってそうであり、事後確率を計算するにはengine.marginal()でなく別のメソッドを使わないといけないのかとも思ったが、よくわからなかった。

Pythonを諦めてツールを探すと、Wekaでできることがわかった。Wekaは機械学習の勉強をするなら必修らしく、過去にインストールしていたので、やってみた。
Wekaを起動して、Tools->Bayes net editorを開くと、GUIがバグだらけ（Version 3.8.1, WindowsとMacとで確認）で使いにくいが、ノードを追加して右クリックしながらネットワークを作成し、Tools->Layoutでノードの配置を修正し、CPTを設定し、さらに保存したXMLを書き換えて色々修正し、Tools->Show Marginsを選ぶと、次のように結合確率が表示される。

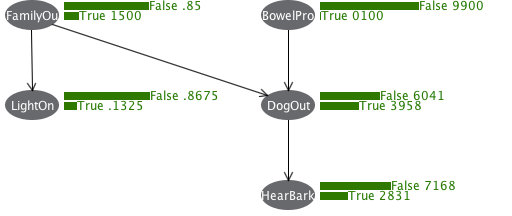
さらに、右クリック->Set evidenceで LightOn=True, HearBark=True と設定すると、次のように、各ノードの事後確率が表示される。

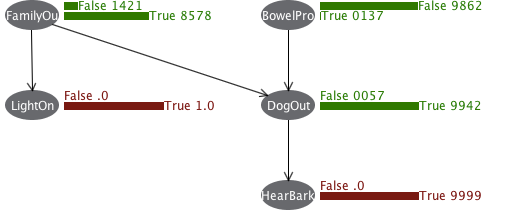
これによると、FamilyOut=Trueの事後確率はやはり0.8578...である。筆者は何か問題を読み間違えているのだろうか？

Weblog on mebius.tokaichiba.jp

Wekaでベイジアンネットワークの事後確率を計算

コメント