ROC曲線を理解する

2値の予測（判別、識別、...）に用いる特徴量の良し悪しを評価する1つの方法として、ROC曲線というものがある。
実際は正で予測も正であるデータの数をTP(True Positive)、
実際は負で予測も負であるデータの数をTN(True Negative)、
実際は負で予測は正であるデータの数をFP(False Positive)、
実際は正で予測は負であるデータの数をFN(False Negative)、
と呼ぶ時、
TPR(True Positive Ratio)=TP/(TP+FN)を縦軸、
FPR(False Positive Ratio)=FP/(FP+TN)を横軸、
としたグラフである。

ROC曲線の例
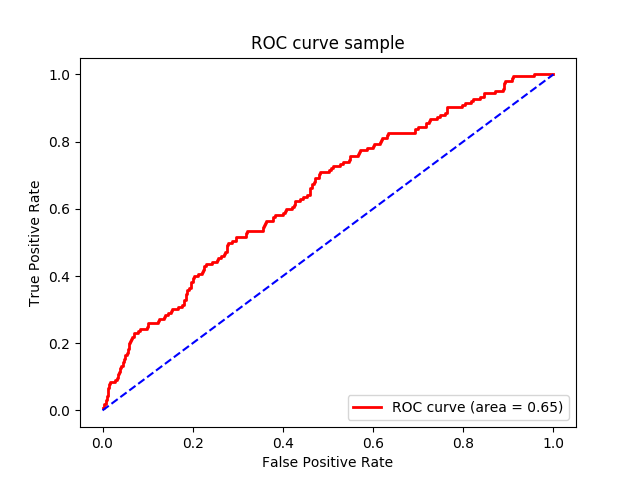
ROC curve sample

ROC曲線は、必ず(0,0)から始まって(1,1)で終わる。
特徴量が全く予測の役に立たない、ランダムな値であれば、TPR=FPRの線になる。
ROC曲線より下の面積、AUR(Area Under ROC curve)（または単にAUC(Area Under the Curve)）が大きいほど、特徴量の値の全域に渡って良い特徴量だとされる。 理想的な特徴量だと、ROC曲線はFPR=0とTPR=1の線になる。

ROC曲線は機械学習で識別器の評価によく用いられるらしいので、とりあえず覚えておこうと思ったのだが、筆者はこれの理解にえらく苦労したので、調べたことや考えたことをメモする。
統計学の検定と同様、こういう確率と論理を組み合わせたものは、人によって向き不向きがあるのだと思いたい。

TP,TN,FP,FNの関係を再度整理すると、次のようになる。

予測
＋−
実
際		＋TPFN (Type II error)
−FP (Type I error)TN
PやNは予測がPositiveかNegativeかであり、TやFはそれが正解かどうかである。
FPは誤検出のことであり、統計学の検定でも使われる「第一種の過誤」（検定では帰無仮説を棄却できないのに棄却する条件に誤ってヒットしてしまうこと）である。
FNは検出不能であり、「第二種の過誤」（検定では帰無仮説が誤りなのに棄却する条件にヒットしないこと）である。

予測の精度に関する尺度としては、Accuracy, Presicision, Recall, F値があり、それぞれ次のように定義される。
Accuracy = (TP+TN) / (TP+TN+FP+FN)
予測の正解率。
Precision = TP / (TP+FP)
Positiveと予測される中の正解率。
Recall = TP / (TP+FN)
実際にPositiveの内、Positiveと予測される割合。検出力、Sensitivity。
F値(F-measure, F1 score) = ((Precision-1 + Recall-1)/2)-1
PrecisionとRecallの調和平均。統計学のF分布に従うF値とは関係ない。
PrecisionとRecallはトレードオフの関係にあるので、それらをバランス良く合成した尺度。

予測の精度はAccuracyで評価するのが簡単だが、実際の正のデータ数と負のデータ数に偏りがあると、データ数が少ない方の正解率が低くても、データ数が多い方の正解率が高ければAccuracyが高くなってしまうので、Accuracyだけでは適切に評価できない。
そのような場合にPrecisionやRecallが用いられるが、これらは一般に特徴量の閾値によってトレードオフの関係があり、セットで評価しないといけないので、単純比較には向かない。そこで用いられるスカラー値が、F値や、ROC曲線のAUCである。
Precision-Recall曲線のAUCも使われることがあるが、Presicionは実際の正のデータの割合に依存するので、正のデータの割合が同じでないと比較には使えない。実際の正のデータの割合が極端に小さい場合など、Precisionが大きな意味を持つ場合にはPrecision-Recall曲線が用いられる。

ROC曲線は、TPR=TP/(TP+FN)とFPR=FP/(FP+TN)のグラフである。TPRを陽性率、FPRを偽陽性率と呼ぶこともある。TPRはRecallと同じである。FPRはfall-out（副産物）と呼ばれることもある。

次の図の3つのROC曲線が、正のデータと負のデータがどのように分布する特徴量に対応するかを考えてみる。
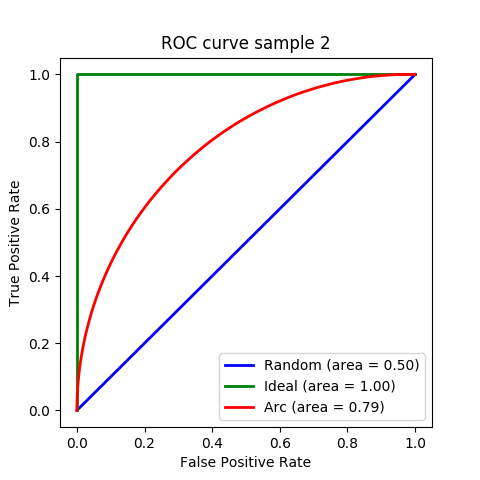
ROC curve sample 2

例えば、次のような分布になる特徴量だと、青いROC曲線になる。
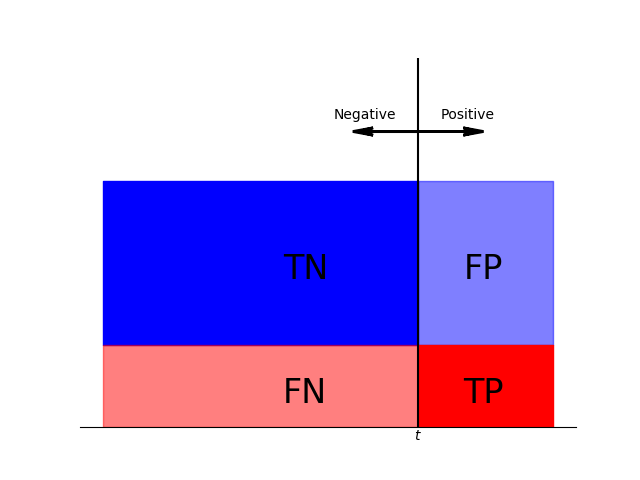
distribution of totally independent feature
横軸は特徴量、縦軸は赤い部分が正のデータの分布、青い部分が負のデータの分布を表している。このグラフでは、正のデータも負のデータも一様分布している。閾値tより右ならPositive、左ならNegativeと予測する時、tを右端から左に動かすと、TPRもFPRも0から1に向かって増大するが、常にTPR=FPRである。正のデータと負のデータの割合はグラフの形状には関係しない。

次のような、正のデータと負のデータが完全に分かれる理想的な特徴量だと、緑のROC曲線になる。
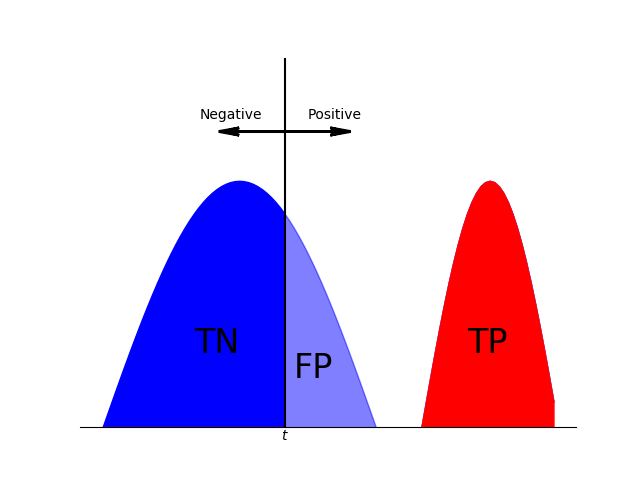
distribution of ideal feature
tを右端から左に動かすと、FPR=0のままTPRが0から1に変化し、青のゾーンに入ると、FPRが0から1に変化する。

次のような分布だと、赤いROC曲線になる。
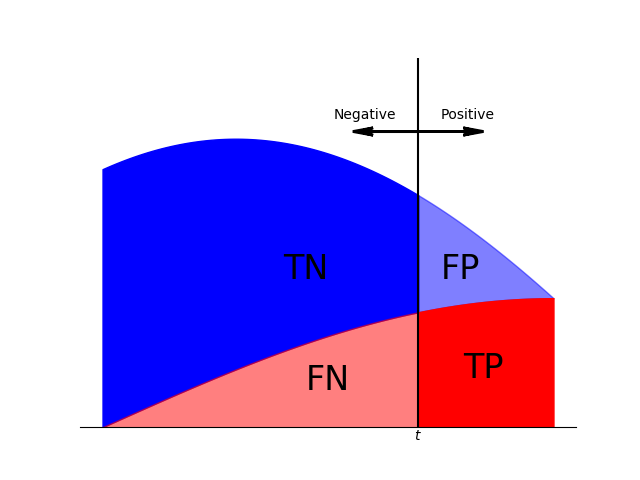
distribution of which makes ROC curve perfect arc
tを右端から左へ動かすと、FPRよりもTPRの方が早く上昇する。なるべく正のデータと負のデータの分布が分離している良い特徴量ほどFPRが上昇する前にTPRが上昇するので、AUCが大きくなることがわかる。

AUCはどれくらいだと良いか、という基準は一般的なものも色々あるようだが、大体、最低0.7は無いと有効ではないとされるようである。

なお、特徴量の最良の閾値(cut-off)はROC曲線の(0,1)に最も近い点とする、という方法を複数の箇所で目にしたが、明確な理論的根拠がある訳ではなく、必ずしもそれに限定されないようである。そもそも、(0,1)に最も近いというのがユークリッド距離で良いのかどうかがわからない。

最後の分布は、ROC曲線が真円の円弧を描くようにしてみた。FPR=1-cosθ、TPR=sinθとなれば良いので、これを微分して左右に圧縮して反転したものを確率密度関数とすれば良いのである。思ったより簡単にできた。

今回のグラフはPython + Matplotlibで作成した。ROC曲線の作成にはscikit-learnも用いた。
それぞれのグラフ作成に用いたソースコードを以下に貼り付ける。

■"ROC curve sample"のグラフ 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc

x = np.random.rand(1000)
y = np.random.randn(1000) > 1.5 - x
fpr, tpr, thresholds = roc_curve(y, x)
roc_auc = auc(fpr, tpr)

plt.plot(fpr, tpr, color='r', lw=2,
         label='ROC curve (area = {:.2f})'.format(roc_auc))
plt.plot([0, 1], [0, 1], color='b', linestyle='--')
plt.title('ROC curve sample')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc='lower right')
plt.show()
■"ROC curve sample 2"のグラフ 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc

def plot_roc_curve(pfunc, nfunc, color, label):
    x = []
    y = []
    for xx in np.arange(0.0, 1.00, 0.01):
        tp = int(100 * pfunc(xx))
        fp = int(100 * nfunc(xx))
        x += [xx] * (tp + fp)
        y += [True] * tp + [False] * fp
    fpr, tpr, thresholds = roc_curve(y, x)
    roc_auc = auc(fpr, tpr)
    plt.plot(fpr, tpr, color=color, lw=2,
             label='{} (area = {:.2f})'.format(label, roc_auc))

plt.figure(figsize=(4.8, 4.8))

plot_roc_curve(lambda x: 1.0/3,
               lambda x: 2.0/3,
               'b', 'Random')

plot_roc_curve(lambda x: (x > 0.7) * np.sin(np.pi*(x-0.7)*10/3),
               lambda x: (x < 0.6) * np.sin(np.pi*x*5/3),
               'g', 'Ideal')

plot_roc_curve(lambda x: (1.0/3)*np.pi/2*np.sin(np.pi/2*x),
               lambda x: (2.0/3)*np.pi/2*np.cos(np.pi/2*x),
               'r', 'Arc')

plt.title('ROC curve sample 2')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc='lower right')
plt.show()
■正負のデータの分布のグラフ 
import numpy as np
import matplotlib.pyplot as plt

def frame_off():
    """no frame, only X axis"""
    ax = plt.gca()
    ax.get_yaxis().set_visible(False)
    ax.get_xaxis().set_visible(False)
    
    ax.spines['top'].set_color('none')
    ax.spines['right'].set_color('none')
    ax.spines['left'].set_color('none')

    # X axis line at y=0
    plt.ylim(0, 1.5)

def fill_plot(f, g, t):
    """paint 0 < y < f(x) in positive color, f(x) < y < g(x) in negative color
       TP, TN: thick color (alpha=1.0)
       FP, FN: thin color (alpha=0.5)
       and put "TP, "FP", "TN", "FN" labels"""

    x1 = np.arange(0.0, t+0.01, 0.01)
    x2 = np.arange(t, 1.0, 0.01)
    plt.fill_between(x1, f(x1) + g(x1), f(x1), color='b', alpha=1.0);
    plt.fill_between(x1, f(x1), color='r', alpha=0.5);

    plt.fill_between(x2, f(x2) + g(x2), f(x2), color='b', alpha=0.5);
    plt.fill_between(x2, f(x2), color='r', alpha=1.0);

    draw_t(t)

def draw_t(t):
    #vertical bar at x=t
    plt.plot([t, t], [0, 1.5], color='k')
    plt.text(t, -0.05, '$t$', ha='center', color='k')

    #notation on the bar
    plt.arrow(t, 1.2, +0.1, 0, fc='k', ec='k', lw=2, head_width=0.03, overhang=0.7)
    plt.arrow(t, 1.2, -0.1, 0, fc='k', ec='k', lw=2, head_width=0.03, overhang=0.7)
    plt.text(t+0.05, 1.25, 'Positive', ha='left')
    plt.text(t-0.05, 1.25, 'Negative', ha='right')

frame_off()
fill_plot(lambda x: 1.0/3,
          lambda x: 2.0/3,
          0.7)

plt.text(0.4, 0.1, 'FN', fontsize=24)
plt.text(0.4, 0.6, 'TN', fontsize=24)
plt.text(0.8, 0.1, 'TP', fontsize=24)
plt.text(0.8, 0.6, 'FP', fontsize=24)

plt.figure()
frame_off()
fill_plot(lambda x: (x > 0.7) * np.sin(np.pi*(x-0.7)*10/3),
          lambda x: (x < 0.6) * np.sin(np.pi*x*5/3),
          0.4)

plt.text(0.3, 0.3, 'TN', ha='right', fontsize=24)
plt.text(0.42, 0.2, 'FP', fontsize=24)
plt.text(0.8, 0.3, 'TP', fontsize=24)

plt.figure()
frame_off()
fill_plot(lambda x: (1.0/3)*np.pi/2*np.sin(np.pi/2*x),
          lambda x: (2.0/3)*np.pi/2*np.cos(np.pi/2*x),
          0.7)

plt.text(0.45, 0.15, 'FN', fontsize=24)
plt.text(0.4, 0.6, 'TN', fontsize=24)
plt.text(0.8, 0.2, 'TP', fontsize=24)
plt.text(0.75, 0.6, 'FP', fontsize=24)

plt.show()