被写界深度の計算式を導いてみた

被写界深度というのは、レンズを通して見た映像の、ピントが合っているように見える、奥行き方向の範囲のことである。
昨年、フォトマスター検定という試験を受ける為に勉強した中で、被写界深度を求める式が何故このようになるのかがわからず、気になっていた。
先月、フォトマスター検定について講義する機会があったので、そのネタとして、被写界深度の式を導いてみた。


図１

まず、被写界深度が何故存在するかというと、ピントが合っていない距離の点は点でなく丸になって映る（ボケる）が、その丸（錯乱円）が十分に小さいと、ほとんどボケてるように見えないからである。
その十分に小さい錯乱円の直径＝許容ボケをδとすると、フィルム（デジカメだとセンサー）上のδに対応して、光軸上のフィルム／センサーの前後に、その範囲に焦点を結ぶとピントが合って見える範囲＝焦点深度が存在する。

図２

この焦点深度の幅を2εとすると、F値（絞り値）＝レンズ焦点距離(f)÷レンズ口径(Φ)を使って、f >> εなのでε/δ = F、すなわちε = Fδと近似できる。
この焦点深度に対応する、被写体側の範囲が、被写界深度である。

ここで、「ガウスの結像公式」（以下、単に「結像公式」）というのを用いる。結像公式とは、凸レンズからa離れた位置から発せられる光が、凸レンズを通って反対側のb離れた位置に焦点を結ぶ時、aとbの関係を、レンズ焦点距離fを用いて、
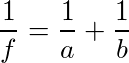
\frac{1}{f}=\frac{1}{a}+\frac{1}{b}, Gaussian form of the lens equation
と表すものである。ちなみに、レンズの焦点距離とは、無限遠から来る光が焦点を結ぶ位置のことである。（上式でa=∞とするとb=fとなる）

この結像公式を用いて、焦点深度と被写界深度の関係を式にする。
図１のように、sをレンズから合焦位置までの距離、snを被写界の近点、sfを被写界の遠点、tをレンズからフィルム／センサーまでの距離とすると、

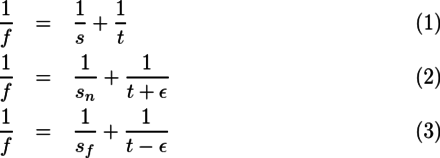
となる。これらの連立方程式を、tを消去して、snとsfについて解く。
(1)よりt=sf/(s-f)が得られるので、これを(2),(3)に代入すると、
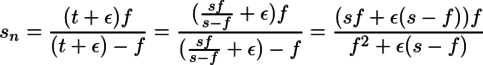
s_n=\frac{(t+\epsilon)f}{(t+\epsilon)-f}=\frac{(\frac{sf}{s-f}+\epsilon)f}{(\frac{sf}{s-f}+\epsilon)-f}=\frac{(sf+\epsilon(s-f))f}{f^2+\epsilon(s-f)}
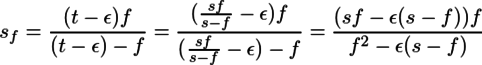
s_f=\frac{(t-\epsilon)f}{(t-\epsilon)-f}=\frac{(\frac{sf}{s-f}-\epsilon)f}{(\frac{sf}{s-f}-\epsilon)-f}=\frac{(sf-\epsilon(s-f))f}{f^2-\epsilon(s-f)}
が得られる。
ここで、s,f>>εなので、s±ε≈s, f±ε≈f, sf±ε2≈sfと近似できることを用いて、簡略化する。
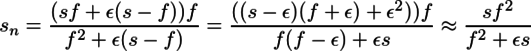
s_n=\frac{(sf+\epsilon(s-f))f}{f^2+\epsilon(s-f)}=\frac{((s-\epsilon)(f+\epsilon)+\epsilon^2))f}{f(f-\epsilon)+\epsilon s}\approx\frac{sf^2}{f^2+\epsilon s}
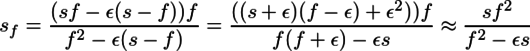
s_f=\frac{(sf-\epsilon(s-f))f}{f^2-\epsilon(s-f)}=\frac{((s+\epsilon)(f-\epsilon)+\epsilon^2))f}{f(f+\epsilon)-\epsilon s}\approx\frac{sf^2}{f^2-\epsilon s}

これにε=Fδを代入すれば、被写界深度の近点と遠点を求める式になるのだが、フォトマスター検定の参考書では過焦点距離を用いた式になっているので、もう少し変形を進める。
過焦点距離とは、被写界深度の遠点が無限遠に届く、最短の撮影距離である。焦点深度と結像公式を用いて被写界深度の近点、遠点と同じ要領で、過焦点距離Hについても式を立てると、

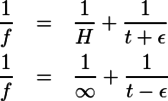
となる。下の式からt=f+εが得られ、それを用いて上の式をHについて解くと、
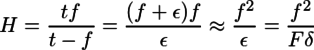
H=\frac{tf}{t-f}=\frac{(f+\epsilon)f}{\epsilon}\approx\frac{f^2}{\epsilon}=\frac{f^2}{F\delta}
すなわち過焦点距離＝レンズ焦点距離2÷（絞り値×許容ボケ）と求まる。これを用いてsn, sfをさらに整理する。
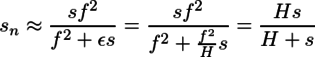
s_n\approx\frac{sf^2}{f^2+\epsilon s}=\frac{sf^2}{f^2+\frac{f^2}{H}s}=\frac{Hs}{H+s}
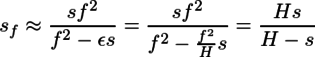
s_f\approx\frac{sf^2}{f^2-\epsilon s}=\frac{sf^2}{f^2-\frac{f^2}{H}s}=\frac{Hs}{H-s}

従って、
被写界近点＝（過焦点距離×合焦距離）÷（過焦点距離＋合焦距離）
被写界遠点＝（過焦点距離×合焦距離）÷（過焦点距離−合焦距離）
である。

なお、過焦点距離の計算には許容ボケが必要になるが、許容ボケは通常、フィルムやセンサーの対角線長÷1300、が用いられる。
35mmフィルムなら、√(362+242)/1300≒0.03328 (≒1/30) mm、
フォーサーズ／マイクロフォーサーズなら√(17.32+132)/1300≒0.01665 (≒1/60) mm、である。