n個のサイコロの目がk種類になる確率

次のような感じの確率を求めようとしたら、泥沼にはまった。

Q: サイコロをn回振った時、出る目がk種類になる確率は？

A:
k=1の確率は、n回全て同じ目で、その目は6通りあるから、6/(6n)である。
k=2の確率は、場合の数が（n回全てaかbの場合 − n回全てaまたはn回全てbの場合）×（(a,b)の組み合わせ）だから、(2n-2)(6C2)/(6n)である。
k=3の確率は、場合の数が（n回全てaかbかcの場合 − n回全てaかbの場合 − n回全てbかcの場合 − n回全てcかaの場合 ＋ n回全てaまたはn回全てbまたはn回全てcの場合）×（(a,b,c)の組み合わせ）だから、(3n-3*2n+3)(6C3)/(6n)である。
つまり、k種類の値を固定した時の場合の数が包除原理に従っているので、答は
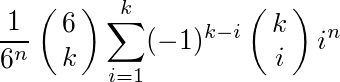
\frac{1}{6^n}\pmatrix{6 \cr k}\sum_{i=1}^k(-1)^{k-i}\pmatrix{k \cr i}i^n
である。（括弧内に2つの数字が縦に並んでるのは二項係数、(6 k)は6Ckと同じ）


サイコロの目の数6をmに一般化して整理すると、等しい確率でm通りの値を取るn個の変数の値がk種類となる確率P(m,n,k)は
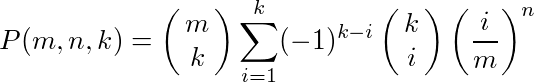
\pmatrix{m \cr k}\sum_{i=1}^k(-1)^{k-i}\pmatrix{k \cr i}\left(\frac{i}{m}\right)^n
となる。

意外にも、Coupon Collector's Problemをさらに複雑にしたような問題であった。
それにしても、(-1)nはいつ見てもむし暑い。