秘書問題の考察(4) 最小期待順位の極限値について

前回のエントリーで説明した、秘書問題(secretary problem)の期待順位を最小にする解に関して、もう少し追究する。


まず、前回は参考文献を鵜呑みにした、j人中x位の人がn人中何位であるかの期待値が
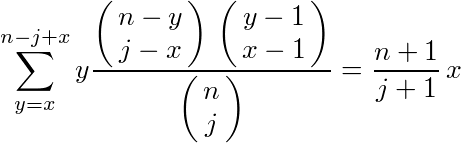
¥sum_{y=x}^{n-j+x}y¥frac{¥pmatrix{n-y¥cr j-x}¥,¥pmatrix{y-1¥cr x-1}}{¥pmatrix{n¥cr j}} = ¥frac{n+1}{j+1}¥,x
となること（左辺が右辺に等しくなること）を導出する。
これの左辺をy(j,x,n)と書く。j人中x位の人は、もう1人加えて(j+1)人とすると、x位か(x+1)位かのどちらかになる。(j+1)人目が上位x位に入ると(x+1)位、入らないとx位のままである。このことから、j人中x位の人の最終順位は(j+1)人中(x+1)位の人の最終順位と(j+1)人中x位の人の最終順位で表され、
y(j,x,n) = x/(j+1) y(j+1,x+1,n) + (j+1-x)/(j+1) y(j+1,x,n)
の関係が成り立つことがわかる。扱いやすいように、jを1つずらして、
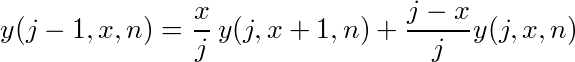
y(j-1,x,n)=¥frac{x}{j}¥, y(j,x+1,n) + ¥frac{j-x}{j} y(j,x,n)
としておく。
y(n,x,n)=xは自明だから、そこからy(n-1,x,n)が求まり、再帰的に計算するとy(j,x,n)が求まる。
j=n-1については、
y(n-1,x,n) = ¥frac{x}{n}(x+1) + ¥frac{n-x}{n} x = ¥frac{n+1}{n}x
j=n-2については、
y(n-2,x,n) = ¥frac{x}{n-1}¥frac{n+1}{n}(x+1) + ¥frac{n-1-x}{n-1}¥frac{n+1}{n}x = ¥frac{n+1}{(n-1)n}¥left(x(x+1)+(n-1-x)x¥right)=¥frac{n+1}{(n-1)n}nx=¥frac{n+1}{n-1}x
なので、y(j,x,n) = (n+1)/(j+1) xではないかと予想できる。それを帰納法で確認する。
j=n-1, n-2については上のように成り立つ。あるjについて成り立つとすると、
y(j-1,x,n) = ¥frac{x}{j}¥frac{n+1}{j+1}(x+1) + ¥frac{j-x}{j}¥frac{n+1}{j+1}x = ¥frac{n+1}{j(j+1)}¥left(x(x+1)+(j-x)x¥right)=¥frac{n+1}{j(j+1)}(j+1)x=¥frac{n+1}{j}x
となり、(j-1)についても成り立つので、間違いなくy(j,x,n) = (n+1)/(j+1) xである。


次に、Chowという人の1964年の論文によるらしい、その筋では頻出の、筆者を秘書問題地獄に陥れたミラクルな定理を紹介する。
定理：期待順位最小の最適戦略による期待順位をV(n)とすると、
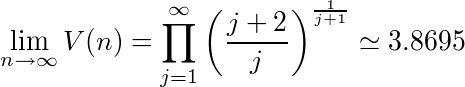
¥lim_{n¥rightarrow¥infty}V(n)=¥prod_{j=1}^{¥infty}¥left(¥frac{j+2}{j}¥right)^¥frac{1}{j+1}¥simeq3.8695
である。
つまり、応募者が何人に増えようが、千人だろうが１万人だろうが、平均的にその中の3.87位以上の人を選択できる採用戦略が存在するのである。その数字の小ささもさることながら、その数字がnを含まないある定数に収束するというのは驚きではなかろうか。

さらに、期待順位最小の最適戦略を、r(x,n)番目の応募者からは暫定x位以上の人を採用すると書くと、次の式が成り立つ。
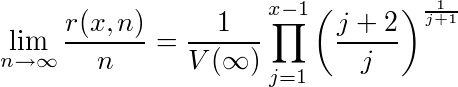
¥lim_{n¥rightarrow¥infty}¥frac{r(x,n)}{n}=¥frac{1}{V(¥infty)} ¥prod_{j=1}^{x-1}¥left(¥frac{j+2}{j}¥right)^¥frac{1}{j+1}
r(x,n)/nは面接した応募者の割合だから、nが大きい時、全応募者のどれくらいの割合を面接した時点から何位以上の人を選べば良いかというのが、これで計算できる。x=1〜10について計算すると

xr(x,n)/n
10.2584
20.4476
30.564
40.6408
50.6949
60.735
70.7658
80.7903
90.8101
100.8265
となるので、最初の25.8%の人はパスし、25.8%の人が過ぎたら1位の人を、44.7%の人が過ぎたら2位以上の人を、56.4%の人が過ぎたら3位以上の人を（以下略）採用すれば良いということになる。（但し、これはnが小さい場合は正確な値との差が大きい。前回のエントリーでの計算結果と比較すると、n=20でもかなりずれている。）

参考文献
Optimal Stopping and Applications（最適停止理論の大家、Thomas S. Ferguson教授による解説）のChapter 2.

それがどうしたと言われようが、筆者が秘書問題から抜け出すためには、この定理のことを書かずには居られなかったのである。
この定理の導出過程を少し覗いてみたいと思ったが、インターネット上を結構探し回ったが、無料で公開されている文書には見つけられなかった。有料の論文を入手しないと見れないようである。

前半の最終順位の期待値の計算に関しては、「超幾何分布」の平均を求めるのと同じ要領で、左辺のΣが1になるように整理して、力ずくで右辺に変形できるものと思っていたが、どうやら思い違いだったようだ。左辺のΣ内は(1/x)倍または(ny/j)倍するとずばり「超幾何分布」の確率密度関数であり、もしxを動かしてΣするとΣ=1なのでΣ部分を消去できるのだが、Σで動かす値が違った。
参考：超幾何分布の平均の求め方
n人からj人選んだ時のy位以上の人数をXとすると、Xは超幾何分布HG(n,j,y)に従う。このXの平均は、
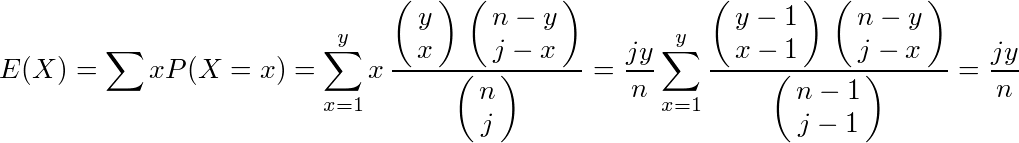
E(X)=¥sum xP(X=x)=¥sum_{x=1}^{y} x¥, ¥frac{¥pmatrix{y¥cr x}¥,¥pmatrix{n-y¥cr j-x}}{¥pmatrix{n¥cr j}} = ¥frac{jy}{n}¥sum_{x=1}^{y} ¥frac{¥pmatrix{y-1¥cr x-1}¥,¥pmatrix{n-y¥cr j-x}}{¥pmatrix{n-1¥cr j-1}} = ¥frac{jy}{n}
となる。（２項係数の変形はaCb=(a/b)*(a-1)C(b-1)を使用、最後の消えるΣの中身はHG(n-1,j-1,y)の確率なので全て足すと1）

今回使ったMaximaの入出力
(%i**) V: 3.8695;
r(x) := 1/V * product((1+2/j)^(1/(j+1)),j,1,x-1);
fpprintprec:4;
makelist(r(x),x,1,10),numer;
(%o**) [.2584,.4476,0.564,.6408,.6949,0.735,.7658,.7903,.8101,.8265]