正20面体の頂点座標を簡単に求める方法があることがわかった。

同じ長方形3枚をこのように組み合わせて、近い頂点を結ぶと、何か20面体ができる。これの長方形の長辺と短辺の比を変えていくと、2つの長方形から3点取った三角形がどこかで正三角形になる。


その時、20面体の30本の辺の長さが全て同じになるので、その時の3つの長方形の頂点が正20面体の頂点である。
長方形の短辺の長さを2、長辺の長さを2xとし、点A〜Eを
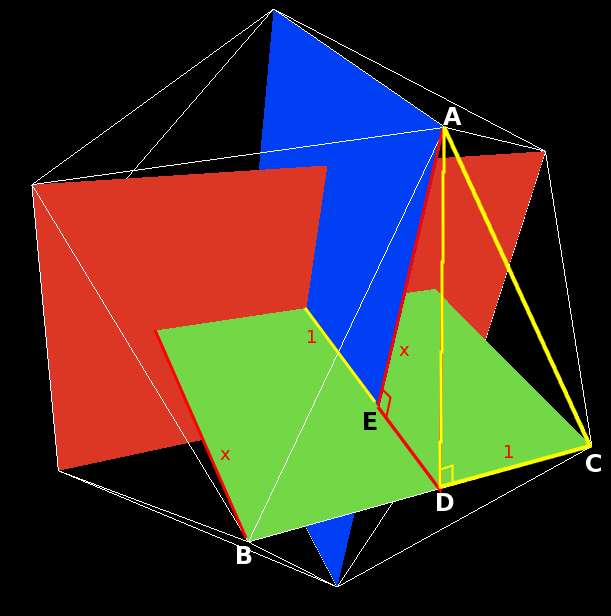
このように取ると、AE=x、ED=(x-1)なので、AD2=x2+(x-1)2であり、DC=1なので、AC2=AD2+DC2=x2+(x-1)2+1である。ABCが正三角形の時、AC=2なので、
x2+(x-1)2+1=4
が成り立ち、これを解くとx=(1+√5)/2(=黄金比)が求まる。
従って、Gを黄金比とすると、
(±1,±G,0)
(0,±1,±G)
(±G,0,±1)
の12点が、1つの正20面体の全ての頂点となる。
一応いつものJava3Dで描いてみた。
Javaアプレットの起動ページへ
確かに正20面体のようである。
以前にJava3Dで正20面体や正12面体を描いてみたが、その時はそれらの多面体の頂点をスマートに求める方法がわからず、中心から各面までの距離や、隣り合う面の法線間の角度を計算する方法を考えるのに何時間もかかった。こんなに簡単な方法があったとはショックである。こういうのはどうやったら思い付けるのだろう。
これなら数分で計算できるので、大学入試とかの問題に普通にありそうな感じかする。
コメント