Maximaでドラゴンカーブ

MathematicaとかMapleとかの数式処理ソフトは、何であんなに高いのだろう。2008/7/26現在、個人向けライセンス価格はMathematicaは40万円超え、Mapleも30万円超えだ。教育機関にも政府機関にも属していない、日曜数学ファンの私にはとても手が出せない。
会社でも研究職とかでなく、ソフトウェア開発の付帯業務をやってるので、数学は一切使っておらず、買ってもらえる見込みは無い。バグ収束曲線が云々で必要とか言っても、そんな統計処理ならExcelで十分と言われてしまうであろう。
従って、MathematicaやMapleに触れる機会が無い。

そんな折、Maximaというフリーの強力な数式処理ソフトがあることを知ったので、今回ヤボ用があって、インストールして使ってみた。
とりあえず、テーラー展開させてみる。 

 KURO-BOX> maxima

Maxima 5.10.0 http://maxima.sourceforge.net
Using Lisp GNU Common Lisp (GCL) GCL 2.6.7 (aka GCL)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
This is a development version of Maxima. The function bug_report()
provides bug reporting information.
(%i1) taylor(sin(x),x,0,10);
                          3    5      7       9
                         x    x      x       x
(%o1)/T/             x - -- + --- - ---- + ------ + . . .
                         6    120   5040   362880
(%i2) taylor(sqrt(r^2-y^2),y,0,10);
                    2      4      6         8       10
                   y      y      y       5 y     7 y
(%o2)/T/       r - --- - ---- - ----- - ------ - ------ + . . .
                   2 r      3       5        7        9
                         8 r    16 r    128 r    256 r
(%i3)
まあ言いたいことは十分わかるが、表示がなんか残念だ。
そこで、満足のいく表示を得るためにTeXmacsを使ってみる。以下の画面はMaxima 5.11.0とTeXmacs 1.0.6.11を使って実際に表示されたものである。%i??という青い部分が入力した部分だ。（表示環境はFreeBSD 6.3+Xorg 1.4.0）

積分もしてみる。

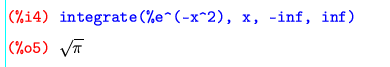
e^(-x^2)を-∞から+∞まで積分すると√πになるのは、手計算でやると面積分にして極座標変換してと技を尽くして偶然解ける感じの有名な例題だが、Maximaは区分求積による近似値計算ではなく、あっさり解析的に計算したようだ。

せっかくTeXmacsを使ってるので、見た目が派手な連分数を表示してみる。

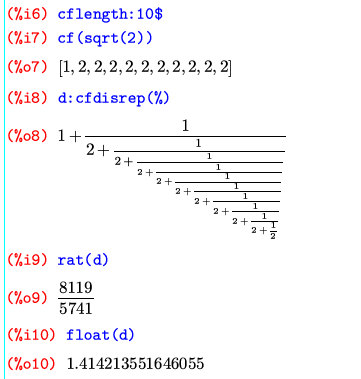
cf(continued fraction)の出力は連分数のリスト表記になっていて、それをcfdisrepすると連分数表記になる。それをratで実数にすると（無限の連分数でないので元々実数だが）約分され、floatで小数にすると元の√2に限りなく近いことがわかる。
蛇足だが、cfdisrepしないと実数や小数に変換できない。

√3についてもやってみる。

方程式を解いてみる。solveで方程式を解析的に解ける。

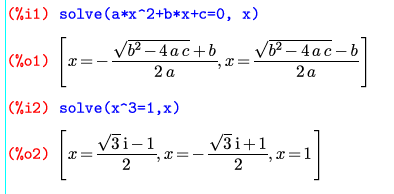
解けない場合は、xの解にxが混ざったりする。（例は省略）

allrootsを使うと、多項式の方程式を数値的に計算できる。

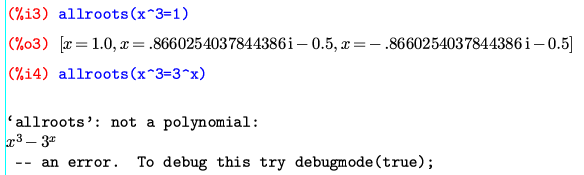
指数の方程式を渡すと文句を言われる。

find_rootを使うと、（おそらくニュートン法による）近似計算で、解が１つだけ含まれる範囲の解を計算できる。

x^3=3^xのe～100の間の解は当然3なのだが、誤差が出た。


さて、せっかくフリーソフトなので、参考資料も無料のものを、と思って、図書館でMaximaの本を探したら、無かった。その代わり、あるMathematicaの本で、わずか十数行のコードでドラゴンカーブ（ドラゴン曲線）を描くMathematicaのコードを見つけた。マンデルブロー集合とかペアノ曲線とかのフラクタル図形の簡単なやつだ。Maximaの練習とMathematicaとの比較を兼ねて、その本を参考にMaximaで似たようなコードを書いてみた。 

dragon(segments_):= block([p, q, r, s],
 p: map(
  lambda([x], [
   [x[1][1], x[1][1] + (x[1][2] - x[1][1]) * (1-%i)/2, x[1][2]],
   [x[2][1], x[2][1] + (x[2][2] - x[2][1]) * (1+%i)/2, x[2][2]]
  ]), segments_),
 q: map(
  lambda([x], [
   {[x[1][1], x[1][2]], [x[1][2], x[1][3]]},
   {[x[2][1], x[2][2]], [x[2][2], x[2][3]]}
  ]), p),
 r: map(lambda([x], listify(x)), flatten(q)),
 s: map(lambda([x], [realpart(x), imagpart(x)]), flatten(r)),
 plot2d([discrete, float(s)],
  [gnuplot_preamble, "set xrange [-1.2:1.2];set yrange [-1.2:1.2]"]),
 r
)$

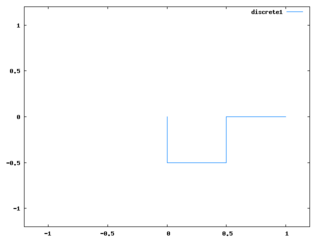
p: [[[0, 1/2-%i/2], [1/2-%i/2, 1]]]$
for i:1 thru 10 do p:dragon(p)$
gnuplotが使える環境でこれを実行すると、以下のようなドラゴンカーブが描かれる。TeXmacsは必要ない。順に、L字型に配置した２本の線から始めて、全体を90°回転させて先端に繋げる、というのを1回、2回、…10回繰り返したものである。
アルゴリズムとしては、全ての線をL字に折り曲げる、というのを繰り返せばドラゴンカーブと同じ形になるというのを使っている。必要最小限にコードを簡略化して難解になったし、同様のアルゴリズムの説明は多くあると思うので、ここではコードの説明は省く。

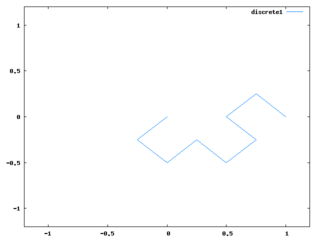
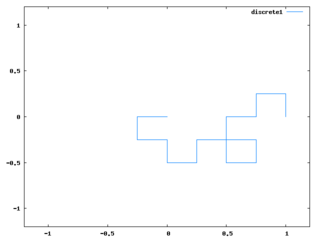
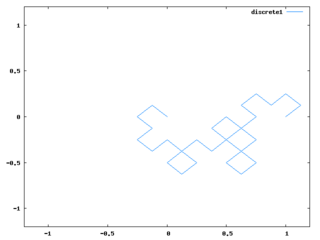
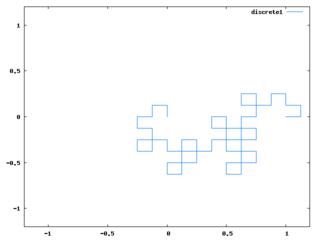
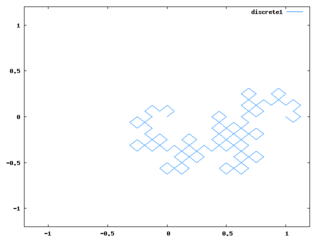
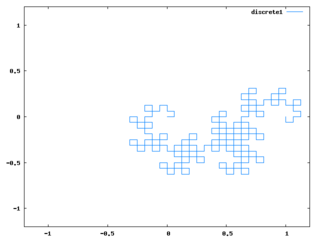
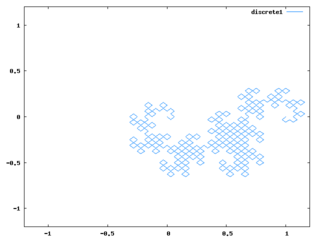
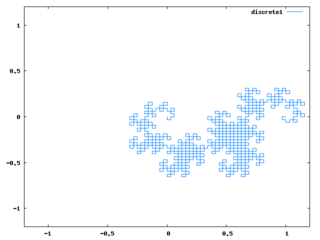
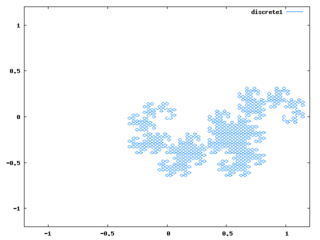
段階が進むと上記コードの処理時間がやたら長くなるので、Perl的発想で、mapしまくって余計なリストを作ってるからかと思って、なるべくリストを作らないように、以下のような２つのコードを作って試してみた。 

dragon2(segments_):= block([p, q, x, s],
 p: map(
  lambda([x], [
   [x[1][1], x[1][1] + (x[1][2] - x[1][1]) * (1-%i)/2, x[1][2]],
   [x[2][1], x[2][1] + (x[2][2] - x[2][1]) * (1+%i)/2, x[2][2]]
  ]), segments_),
 q: [],
 for x in p do q: append(q, [
   [[x[1][1], x[1][2]], [x[1][2], x[1][3]]],
   [[x[2][1], x[2][2]], [x[2][2], x[2][3]]]
  ]),
 s: map(lambda([x], [realpart(x), imagpart(x)]), flatten(q)),
 plot2d([discrete, float(s)],
  [gnuplot_preamble, "set xrange [-1.2:1.2];set yrange [-1.2:1.2]"]),
 q
)$
dragon3(segments_):= block([p, p1, p2, x, s],
 p: [],
 for x in segments_ do (
  p1: x[1][1] + (x[1][2] - x[1][1]) * (1-%i)/2,
  p2: x[2][1] + (x[2][2] - x[2][1]) * (1+%i)/2,
  p: append(p, [
   [[x[1][1], p1], [p1, x[1][2]]],
   [[x[2][1], p2], [p2, x[2][2]]]
  ])
 ),
 s: map(lambda([x], [realpart(x), imagpart(x)]), flatten(p)),
 plot2d([discrete, float(s)],
  [gnuplot_preamble, "set xrange [-1.2:1.2];set yrange [-1.2:1.2]"]),
 p
)$
結果は、少しずつは速くなったが、18.9秒が18.6秒とか18.0秒になるくらいで、ほとんど変わらなかった。余計なことはせず全て任せとけと言われた気分になった。Lispのリストの作成と削除は重くないらしい。CやPerlのような手続き型言語とは特性が違うのかも知れない。

さて、Mathematicaと比較すると、Maximaはわかりやすい参考資料が少ないのが非常につらい。taylorやintegrateの説明は当たりがつくのですぐに見つかったが、何かにつけ、どこを探せばいいのかがわからない。
今回MathematicaのNSolveに相当するfind_rootを見つけるのにもかなり時間がかかった。MathematicaのFlattenに相当するものが見つからず（Maximaのflattenは何重のリストでも全展開になる）、ドラゴンカーブのコードを実現するために数時間かけて解決策をひねり出したが、スマートなコードにならなかった。gnuplot関係はカットアンドトライでなんとか動いたが、結局わからないことだらけだ。
また、エラーメッセージが一昔前のCコンパイラ並に不親切で、エラーが出ると根本原因を見つけるのに一苦労でうんざりする。

しかし、MathematicaもMaximaも深くは知らないが、数式処理に関しては今の所MathematicaにできてMaximaにはどうしてもできないようなことは見当たらず、Maximaは非常に強力だと思った。Lispで書かれていることと合わせて、その出来栄えはフリーソフトとしては驚異的だと思う。