Maximaで微分方程式

せっかくMaximaを使い始めたので、慣れるためにさらにMaximaのマニュアルを読み進めて遊んでると、Maximaは微分方程式も解けることがわかった。難しそうな響きを擁して実際難しい、物理学の基本ツールである。一瞬気が進まなかったが、大したものだと思ったので、敬意を表して試してみた。
すると、微分方程式が見えた気分になるようなグラフが出せることがわかり、面白かったので、ここに書き記すことにした。

まず、コマンドラインで微分させてみる。diff()が微分演算だ。

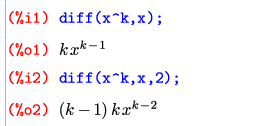
例によってTeXmacsを使って出力を整形している。(%i??)に続く青い部分が入力した部分、(%o??)に続く黒い部分がMaximaの出力だ。diff()の2つ目の引数は何で微分するか、3つ目の引数（省略可）は何回微分するかを意味する。

次に、desolve()を使ってシンプルな微分方程式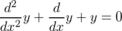\frac{d^2}{dx^2}y+\frac{d}{dx}y+y=0を解かせてみる。

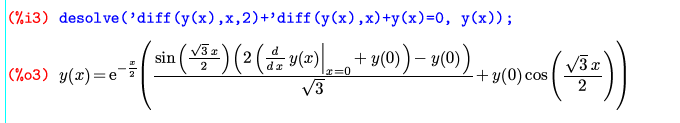
desolve()の2つ目の引数は、どの関数について解くかを示す。diffの前の'（アポストロフィー）は、そのLisp関数を評価（実行＆展開）せず、そのまま渡すことを指示するものである（desolve()の場合はこれを省略して評価してしまっても良いようだが、後述のode2()では不可）。y(x)の(x)はyがxの関数であることを示し、これを省略するとdy/dxが0になってしまう。
atvalue()を使って、y,y'の初期値を与えてから再度解かせてみる。

入力行の行末に;の代わりに$を付けると、計算結果を出力しない。
念のため、元の方程式に当てはまるかどうか、検算してみる。

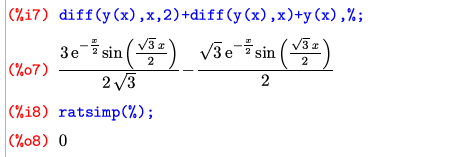
%は直前の計算結果を表す。%o7は見るからに0なのだが、なぜか計算してくれなかったので、ratsimp()で整理させた。

常微分方程式（未知関数が１つだけの微分方程式）はode2()を使って解く方法もある。ode2()を使う場合、初期値は一般解の計算結果に対してic1(),ic2(),bc2()などを使って与える。同じ方程式を解かせてみる。

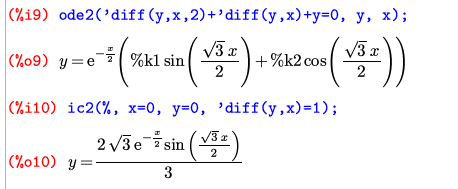
ode2()の2つ目の引数は常微分方程式の未知関数、3つ目の引数はその関数が従属する変数だ。上の場合は、引数からyがxの関数であることがわかるので、yをy(x)と書かなくても良い。

desolve()とode2()の能力を比較するため、解くには少し難しそうな微分方程式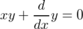xy+\frac{d}{dx}y=0を解かせてみる。

ode2()は難なく解いた。念のため検算しておく。

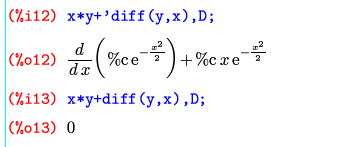
それに対して、同じものをdesolve()に解かせると、下のような奇妙な式になった。

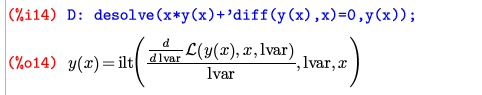
おそらく、ラプラス変換してx,yについて解いてラプラス逆変換したもの、という意味なのだろうが、これでは使えないだろう。これでも使える解なのかどうかを一応確認してみる。

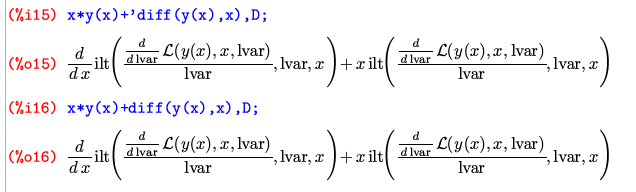
やはり解けていない、使えない解であることがわかる。常微分方程式を解くのはdesolve()よりode2()の方が優れているようだ。

しかし、desolve()は複数の未知関数を含む連立微分方程式も解ける。
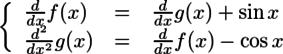
\left\{ \begin{array}{lll} \frac{d}{dx}f(x) & = & \frac{d}{dx}g(x)+\sin{x} \\ \frac{d^2}{dx^2}g(x) & = & \frac{d}{dx}f(x)-\cos{x} \end{array} \right.

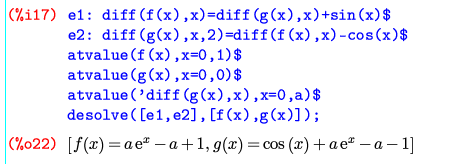
e1とe2が方程式、f(x)とg(x)が未知関数だ。desolve()には、上のように、方程式と未知関数をそれぞれリスト形式で与える。

次に、plotdf()を使って微分方程式のグラフを出してみる。plotdf()に与える微分方程式は、dy/dx=F(x,y)または[dx/dt, dy/dt]=[F(x,y), G(x,y)]に限定されている。

load("plotdf");
plotdf(x);
これを実行すると、下のような画面が開く。（FreeBSD 6.xではTcl/Tkをインストールしていても「wishが無い」というエラーが出たが、wishという名のwish?.?へのリンクを作ればOKだった）

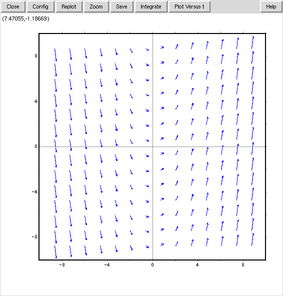
たくさんある矢印は、その地点(x,y)におけるdy/dxの向きと大きさを表している。このグラフ上のどこかをクリックすると、その座標を初期値とするグラフが描かれる。下の図は(0,0)辺りをクリックしたもの。

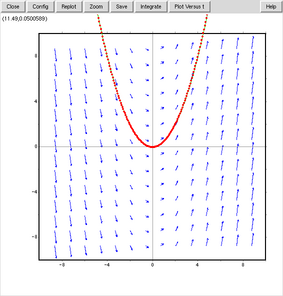
さらに色々な所をクリックする。

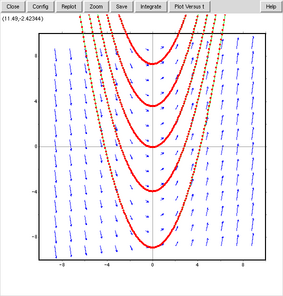
次の2つの図は、

plotdf(sin(x));
を実行したものである。

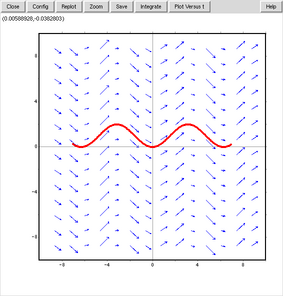
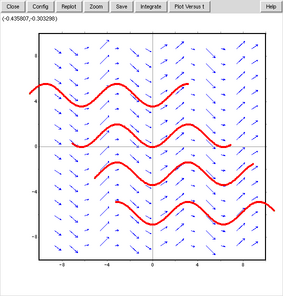
xとyを含む式も試してみる。

plotdf(sin(x)+cos(y));

放物線を横にした、x=y2を出そうとした。両辺をxで微分すると1=2y(dy/dx)なので、dy/dx=1/(2y)である。よりシンプルに、dy/dx=1/yで試そうとして、

plotdf(1/y);
とすると、原因がよくわからないが、Tclのエラーになった。しかし、次のように小さなオフセットを与えると、何か描画された。2つ目以降の引数に色々なオプションを指定しているが、これらが無くてもエラーにはならない。
plotdf(10^-10+1/y,[trajectory_at,0.5,1],[nsteps,200],[xradius,3],[yradius,6],[xcenter,3],[ycenter,0]);

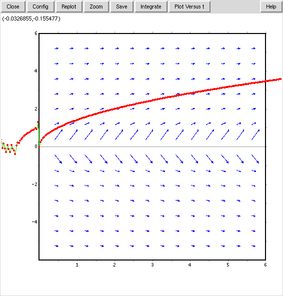
trajectory_atで初期値を(0.5,1)として描画したものだが、左側が何かおかしい。さらに何ヶ所かクリックしてみると、

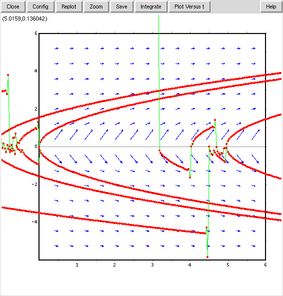
y=0の近辺でおかしくなるようだ。1/(y+⊿y)-1/yの計算でもしているのだろうか。

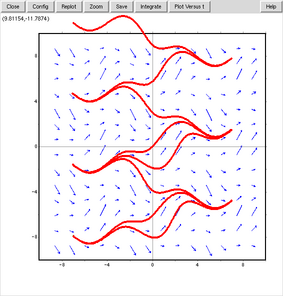
x=cos(t), y=sin(t)のグラフは円になるので、[dx/dt, dy/dt]=[-y,x] (=[-sin(t), cos(t)])のグラフも円になる（図は省略）。それよりもっと場を複雑にさせようと考えて、dx/dtとdy/dtを周期関数にしてみた。次のグラフは[dx/dt, dy/dt]=[sin(y),sin(x)]である。

plotdf([sin(y),sin(x)]);

色を変えながら初期値をクリックした。セル状のグラフが無限に続く。
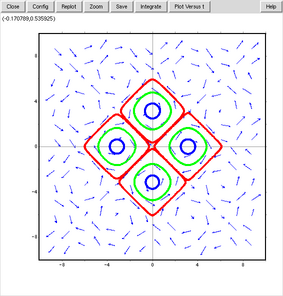
dx/dtとdy/dtを入れ替えると、次のようなグラフになる。
plotdf([sin(x),sin(y)]);

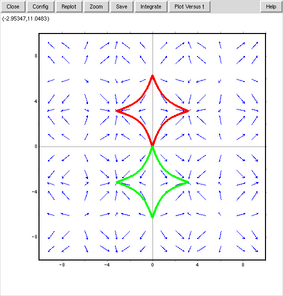
こんなのも作ってみた。

plotdf([
10^-10 - sin(atan(y/x))*cos(%pi/4*sin(8*atan(y/x))) - cos(atan(y/x))*sin(%pi/4*sin(8*atan(y/x))),
10^-10 - sin(atan(y/x))*sin(%pi/4*sin(8*atan(y/x))) + cos(atan(y/x))*cos(%pi/4*sin(8*atan(y/x)))
]);

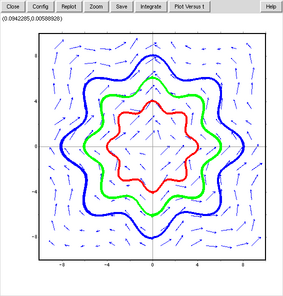
[dx/dt, dy/dt]=[F(x,y), G(x,y)]で表せない（dx/dtにtが入るとか）方程式も、desolve()で解けるものなら
、いつものplot2d()でグラフにできる。
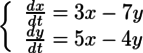
\left\{\begin{array}{l}\frac{dx}{dt}=3x-7y\\ \frac{dy}{dt}=5x-4y \end{array}\right.
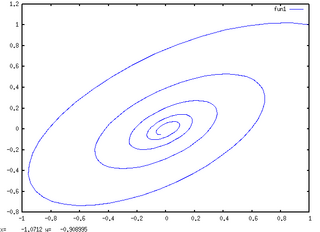
（この方程式は[dx/dt, dy/dt]=[F(x,y), G(x,y)]で表せるが、plotdf()ではおかしなグラフになる）

atvalue(x(t),t=0,1);
atvalue(y(t),t=0,1);
Z:desolve([diff(x(t),t)=3*x(t)-7*y(t), diff(y(t),t)=5*x(t)-4*y(t)],[x(t),y(t)]);
plot2d([parametric, x(t), y(t), [t,0,6]],[nticks,200]),Z;

アステロイド曲線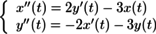\left\{\begin{array}{l} x''(t)=2y'(t)-3x(t)\\ y''(t)=-2x'(t)-3y(t) \end{array}\right.（実はx=cos(t)^3, y=sin(t)^3から逆算したもの）を描いてみる。

atvalue(x(t),t=0,1);
atvalue(y(t),t=0,0);
atvalue(diff(x(t),t),t=0,0);
atvalue(diff(y(t),t),t=0,0);
Z: desolve([
diff(x(t),t,2)=2*diff(y(t),t)-3*x(t),
diff(y(t),t,2)=-2*diff(x(t),t)-3*y(t)
],[x(t),y(t)]);
plot2d([parametric,x(t),y(t), [t,0,2*%pi]],[nticks,200]),Z;

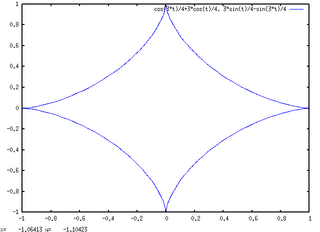
[parametric, ...]の部分を、それらのリストにすることにより、複数のグラフを1枚に描ける。

eq: [
diff(x(t),t,2)=2*diff(y(t),t)-3*x(t),
diff(y(t),t,2)=-2*diff(x(t),t)-3*y(t)
];
atvalue(x(t), t=0, 1);
atvalue(y(t), t=0, 0);
atvalue(diff(x(t), t), t=0, 0);
atvalue(diff(y(t), t), t=0, 0);
Z1: desolve(eq, [x(t), y(t)]);
atvalue(x(t), t=0,2);
Z2: desolve(eq, [x(t), y(t)]);
atvalue(x(t), t=0,3);
Z3: desolve(eq, [x(t), y(t)]);
L1: [parametric, x(t), y(t), [t, 0, 2*%pi]], Z1;
L2: [parametric, x(t), y(t), [t, 0, 2*%pi]], Z2;
L3: [parametric, x(t), y(t), [t, 0, 2*%pi]], Z3;
plot2d([L1,L2,L3], [nticks,200]);

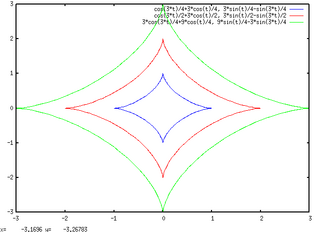
微分方程式は解く過程で積分が入るので、解析的には解けない場合も少なくない。微分方程式を数値的に解く、MathematicaのNDSolveに相当するものがあれば、ずっと便利なのだが、残念ながら無さそうだ。グラフにするかどうかに関係なく、微分方程式を数値的に解けないのは、実用上不都合が多いと思われる。

以下、余談。
筆者は大学時代に制御工学を学んでいて、３～４年の頃はそれこそ来る日も来る日もラプラス変換を使っていたのだが、それで何を解いていたかというと、もちろん微分方程式である。この項を書き始めるまで、そのことをすっかり忘れていて、微分方程式は昔から遠い世界のものと思い込んでおり、今回、自分に微分方程式漬けだった時期があったことを思い出して、驚いた。ああ、あの時必死で勉強したあれが、微分方程式だったのか…と思った。テレビに出てる有名人が、昔会ったことがある人だと判った時のような驚きと言えようか。

ソフトウェアの仕事をやっていると、微分方程式は目にすることも無く、10年以上経って、すっかり忘れてしまった。あれだけやったのだから体が覚えていても良さそうなものと思うのだが、具体的な式は何も思い出せないし、物理的な応用例も何一つ思いつかない。
当時、微分方程式を解いているという感覚はほとんど無く、ラプラス変換の計算方法を覚えて、ラプラス変換された普通のｎ次方程式を解いている感じだった。現実の物理現象に応用することなく、机上で計算だけやっていたから、全然身に付かなかったということだろう。
数学は現実世界の何かや図形のイメージに対応させて理解しないといけないと改めて思った。