余弦定理、正弦定理の導き方

今週、TVで「余弦定理」という言葉を耳にした。高校でそういう公式を習って名前だけは覚えていたが、中身は雰囲気すら思い出せなかった。
15年以上前にセンター試験を受けた時は完璧に暗記していたはずである。三角関数の加法定理は今でも身体が覚えていた。漢字と同じように書き順で覚えていて、右手が紙に書き始めると、何も考えなくても勝手に手が動いて、筆記体のような加法定理を書き終える。ちなみに我が筆記体では+とxは同じ形であった。
倍角の公式や和積・積和の公式や合成の公式（sinθ+cosθ=sin(θ+α)という変形）を加法定理から無事に導き出せて、正弦定理も何とか思い出すことができたのだが、余弦定理は影も形も思い出せなかった。
仕方なく、インターネットで調べた。

●余弦定理

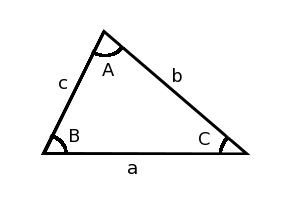
三角形の３辺の長さをa,b,c、各辺の向かい側の角度をA,B,Cとすると、
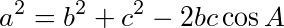
a^2=b^2+c^2-2bc¥cos A
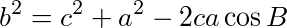
b^2=c^2+a^2-2ca¥cos B
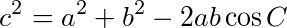
c^2=a^2+b^2-2ab¥cos C
が成り立つ。

●正弦定理
同じく、
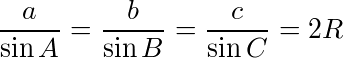
¥frac{a}{¥sin A}=¥frac{b}{¥sin B}=¥frac{c}{¥sin C}=2R
（Rは外接円の半径）が成り立つ。

そうそう、そういえばそんなのがあった。何でそういうのが成り立つのかがわからないまま、丸暗記した記憶がある。何でそうなるんだろう？と、何度も不思議に思った記憶もある。
これらを初めて教わってから20年、ついに導き方を理解した。

●余弦定理の導出

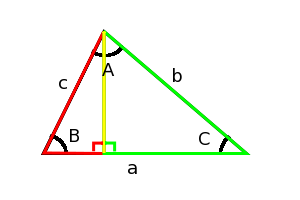
このようにaに垂線を引くと、
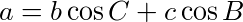
a=b¥cos C+c ¥cos B
の関係があることがわかる。これの両辺を２乗すると、
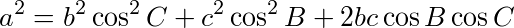
a^2=b^2¥cos^2 C+c^2¥cos^2 B+2bc¥cos B¥cos C
である。sin2+cos2=1やコサインの加法定理
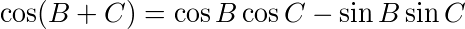
¥cos(B+C)=¥cos B¥cos C-¥sin B¥sin C
を使って整理すると、

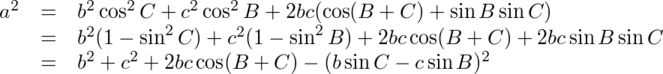
となる。A+B+C=π（180°）だから、
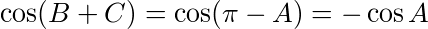
¥cos(B+C)=¥cos(¥pi-A)=-¥cos A
であり、b sinC = c sinB = aへの垂線の長さで末尾の２乗部分は0なので、余弦定理の式が求まる。

●正弦定理の導出

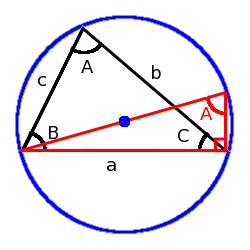
このように同じ外接円を持つ１辺がaの直角三角形を描くと、円周角の定理より、aの向かいの角の角度はやはりAである。また、同じく円周角の定理より、円周角が90°なら中心角が180°なので、斜辺は外接円の中心を通り、長さは直径=2Rに等しい。従って、2R sinA=aである。

簡単ではないか。なぜ高校で教えてくれなかったのだろう。

高校で習った部分積分の公式は、習ったのが高３の半ばだったせいもあるが、覚えられたのは大学に入ってからだった。複雑過ぎて覚える気がしなかったのである。同じように複雑な三角関数の和積・積和の公式は加法定理から導けるので覚える必要が無かったが、部分積分の公式は導き方を教わらなかったので、丸暗記するしか無かった。
大学に入ってから、独自に導き方を編み出した。

積の微分の公式より、
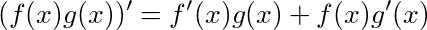
(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)
移項すると
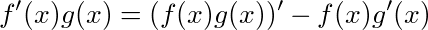
f'(x)g(x)=(f(x)g(x))'-f(x)g'(x)
両辺を積分すると
¥int_a^b f'(x)g(x)dx=¥left[f(x)g(x)¥right]_a^b-¥int_a^b f(x)g'(x)dx

以後、部分積分の公式を覚える必要が無くなったし、10年以上使ってない今もすぐ導き出せる。
ある時、大学で部分積分の公式を思い出すのに手間取っていた同級生に、この導き方のことを言ったら、他の同級生も含めて、誰も知らなかった。理系の学部であり、大学受験の時は皆部分積分の達人だったはずである。誰もそうは教わらなかったということだ。これは数学的には正確でないか何かで、高校ではこのように教えてはいけないものなのだろうか？

筆者は今週余弦定理の導き方を知ったが、これによりあと10年は自力で導ける気がする。数学の公式は、他のものから簡単に導けるものは導き方を教えてくれた方がいいと思う。
でも最初に公式と同時に言われても要点を理解できないか、興味が持てないかも知れないので、ある程度慣れてからというか、公式の使い方を理解して威力を実感してからがいいのかも知れないという気はしなくもない。