円盤の衝突計算

弾性衝突円盤アプレットの衝突計算について、悲しいことに式を求めるのにかなり時間を費やしたので、忘れないように記録する。これが無いと、自分でもソースコードを理解できなくなってしまう。

まず直線上の衝突について考える。物体1,2の質量をm1,m2、衝突前の速度をv1,v2、衝突後の速度をv1',v2'とすると、完全弾性衝突の場合、運動量保存の法則より
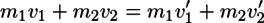
m_1v_1+m_2v_2=m_1v'_1+m_2v'_2
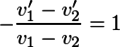
-\frac{v'_1-v'_2}{v_1-v_2}=1
が成り立つ。速度変化に注目してこれを整理すると、
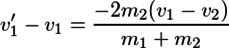
v'_1-v_1=\frac{-2m_2(v_1-v_2)}{m_1+m_2}
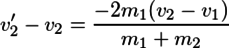
v'_2-v_2=\frac{-2m_1(v_2-v_1)}{m_1+m_2}
が得られる。これは、
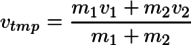v_{tmp}=\frac{m_1v_1+m_2v_2}{m_1+m_2}---(1)
と置くと、
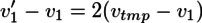v'_1-v_1=2(v_{tmp}-v_1)---(2)
v'_2-v_2=2(v_{tmp}-v_2)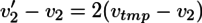---(3)
と整理できる。

次に平面上の衝突について考える。
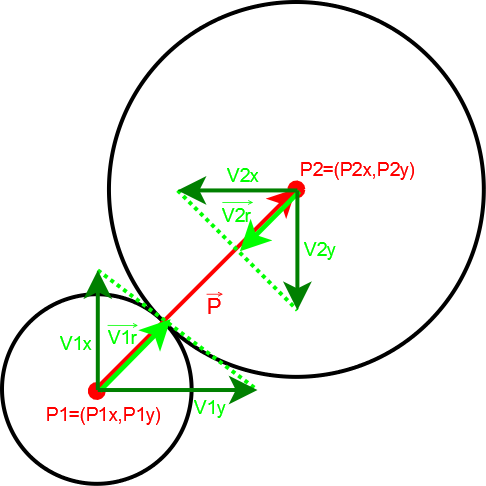
ball_hit.png
図のように円盤と円盤が衝突する場合の速度変化については、円盤の中心同士を結ぶ線上の方向の
速度が衝突によって変化し、衝突方向でない速度成分は変化しないので、衝突方向の速度V1r、V2rについて、上記の式(1)～(3)により速度の変化を求めれば良い。つまり、 Pを円盤の中心間を結ぶベクトル、V1,V2を円盤1,2の速度ベクトル、v1r,v2rを円盤1,2のP方向の速度、V1,v1rの衝突後の速度をそれぞれV1',v1r'とすると、円盤の速度変化は
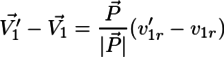
\vec{V'_1}-\vec{V_1} = \frac{\vec{P}}{|\vec{P}|}(v'_{1r}-v_{1r})
である。

v1rの計算については、θをPとV1の間の角度とすると、
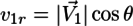
v_{1r} = |\vec{V_1}|\cos{\theta}
であり、PとV1との内積は
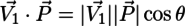
\vec{V_1}\cdot\vec{P} = |\vec{V_1}||\vec{P}|\cos{\theta}
だから、
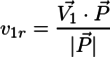
v_{1r} = \frac{\vec{V_1}\cdot\vec{P}}{|\vec{P}|}
で求められる。同様に
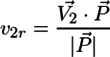
v_{2r} = \frac{\vec{V_2}\cdot\vec{P}}{|\vec{P}|}
となる。

直線の場合の式(1)と同様に
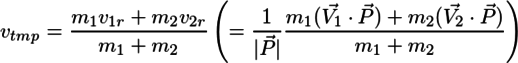
v_{tmp}=\frac{m_1v_{1r}+m_2v_{2r}}{m_1+m_2} \left (=\frac{1}{|\vec{P}|}\frac{m_1<br /> (\vec{V_1}\cdot\vec{P})+m_2(\vec{V_2}\cdot\vec{P})}{m_1+m_2}\right )
と置くと、(2)より
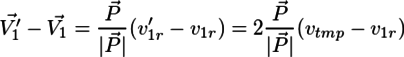
¥vec{V'_1}-¥vec{V_1} = ¥frac{¥vec{P}}{|¥vec{P}|}(v'_{1r}-v_{1r}) = 2¥frac{¥vec{P}}{|¥vec{P}|}(v_{tmp}-v_{1r})
となる。vtmpとv1rの両方に1/|P|が入っているので、計算上の便宜のため、
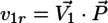
v_{1r} = \vec{V_1}\cdot\vec{P}
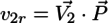
v_{2r} = \vec{V_2}\cdot\vec{P}
と置き直すと、
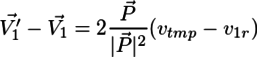
¥vec{V'_1}-¥vec{V_1}=2¥frac{¥vec{P}}{|¥vec{P}|^2}(v_{tmp}-v_{1r})
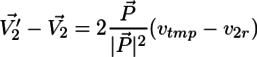
¥vec{V'_2}-¥vec{V_2}=2¥frac{¥vec{P}}{|¥vec{P}|^2}(v_{tmp}-v_{2r})
が得られる。２次元のベクトルをX軸成分とY軸成分に分けて
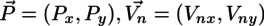
\vec{P}=(P_x,P_y), \vec{V_n}=(V_{nx},V_{ny})
とスカラー表記にすると、
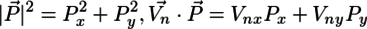
|\vec{P}|^2 = P_x^2+P_y^2, \vec{V_n}\cdot\vec{P}=V_{nx}P_x+V_{ny}P_y
なので、円盤同士の衝突による速度変化は、
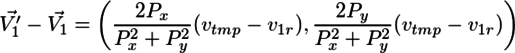
\vec{V'_1}-\vec{V_1} = \left (\frac{2P_x}{P_x^2+P_y^2}(v_{tmp}-v_{1r}),\frac{2P_y}{P_x^2+P_y^2}(v_{tmp}-v_{1r}) \right )
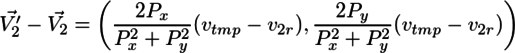
\vec{V'_2}-\vec{V_2} = \left (\frac{2P_x}{P_x^2+P_y^2}(v_{tmp}-v_{2r}),\frac{2P_y}{P_x^2+P_y^2}(v_{tmp}-v_{2r}) \right )
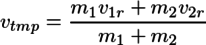
v_{tmp}=\frac{m_1v_{1r}+m_2v_{2r}}{m_1+m_2}
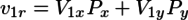
v_{1r} = V_{1x}P_x+V_{1y}P_y
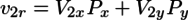
v_{2r} = V_{2x}P_x+V_{2y}P_y
で求められることがわかる。