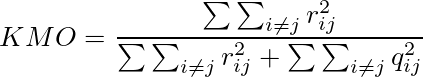Weblog on mebius.tokaichiba.jp

何年も前に買って読んでいなかった「統計学が最強の学問である」シリーズを、今更ながら読んでいる。その［数学編］はほとんど知っている内容だったので、半分くらいは流し読みしたのだが、所々、特に微分・積分以降はわかっているようでわかっていなかったことを思い知らされて勉強になったし、大変面白かった。

さて、p.490のロジスティック回帰の最急降下法の説明の所に、「気になる方はエクセルや何らかのプログラミング言語を使って挑戦していただければと思いますが、...」と書かれている。気にならない訳がないので、やってみた。

問題は、次のようなデータについて、トラブルの有無がどの程度リピート率に影響するかをロジスティック回帰分析で調べるというものである。

利用時間	トラブル	リピート	人数
ランチ	なし	なし	207
ランチ	なし	あり	23
ランチ	あり	なし	18
ランチ	あり	あり	2
ディナー	なし	なし	435
ディナー	なし	あり	290
ディナー	あり	なし	15
ディナー	あり	あり	10

●コード

import numpy as np

# 元データ(p.483)
data = np.array([
    # ディナーダミー、トラブルダミー、リピートダミー、人数
    [0, 0, 0, 207],
    [0, 0, 1, 23],
    [0, 1, 0, 18],
    [0, 1, 1, 2],
    [1, 0, 0, 435],
    [1, 0, 1, 290],
    [1, 1, 0, 15],
    [1, 1, 1, 10]])

# 各行を人数分に展開したもの
data_flat = np.repeat(data[:, :3], data[:, 3], axis=0)

X = data_flat[:, :2] # ディナーダミー、トラブルダミー
X = np.hstack((np.ones_like(X[:,:1]), X)) # 1列目に全て1の列を追加
y = data_flat[:, 2]  # リピートダミー

# コスト関数 C(β) = -log L(β) = - \sum { (y - 1) x^T β - log(1 + exp(-x^T β)) }
# L(β) = \Pi p^y (1-p)^(1-y), p = 1 / (1 + exp(-x^T β))
def cost_function(X, y, beta):
    return -np.sum((y - 1) * (X @ beta) - np.log(1 + np.exp(-X @ beta)))

# 勾配 ∂C/∂β のテスト(p.490)
beta = np.array([1.0, 1.0, 1.0])
delta = 0.0001
gradient = [
    (cost_function(X, y, beta + [delta, 0, 0]) - cost_function(X, y, beta)) / delta,
    (cost_function(X, y, beta + [0, delta, 0]) - cost_function(X, y, beta)) / delta,
    (cost_function(X, y, beta + [0, 0, delta]) - cost_function(X, y, beta)) / delta,
]

print("first gradient =", gradient)

# 勾配が最小になるβを求める
# βから勾配に学習率を掛けたものを引くのを繰り返す
learning_rate = 0.005

for i in range(120):
    gradient = np.array([
        (cost_function(X, y, beta + [delta, 0, 0]) - cost_function(X, y, beta)) / delta,
        (cost_function(X, y, beta + [0, delta, 0]) - cost_function(X, y, beta)) / delta,
        (cost_function(X, y, beta + [0, 0, delta]) - cost_function(X, y, beta)) / delta,
    ])
    beta -= learning_rate * gradient

print("beta =", beta)

# オッズ比(p.492)
print("odds of beta1, beta2 =", np.exp(beta[1:]))

# scikit-learnのLogisticRegressionで検算する
from sklearn.linear_model import LogisticRegression

X = data_flat[:, :2] # ディナーダミー、トラブルダミー
y = data_flat[:, 2]  # リピートダミー

lr = LogisticRegression().fit(X, y)
print("sklearn beta0 =", lr.intercept_, ", (beta1, beta2) =", lr.coef_[0])
print("sklearn odds of beta1, beta2 =", np.exp(lr.coef_[0]))

●実行結果

first gradient = [523.157877723861, 362.3960970844564, 29.430456188492826]
beta = [-2.19686992  1.79119201  0.00347654]
odds of beta1, beta2 = [5.99659623 1.00348259]
sklearn beta0 = [-2.12298445] , (beta1, beta2) = [ 1.70835681 -0.00918478]
sklearn odds of beta1, beta2 = [5.51988382 0.99085727]

betaの1つ目が切片、2つ目と3つ目が回帰係数で、それぞれ小数点第2位を四捨五入すると[-2.2, 1.8, 0.0]、回帰係数をオッズ比にすると[6.0, 1.0]である。p.493の結果と一致した。トラブル有無のオッズ比が1.0なので、リピート率への影響は無しという結果である。
検算の為にscikit-learnのLogisticRegressionでもやってみたら、切片が-2.1、回帰係数の1つ目が1.7と少し違う結果になり、LogisticRegressionのハイパーバラメーターを色々変えてみても本の記載と同じ結果にはできなかった。そういうものなのだろうか。コスト関数の勾配は本の結果の方が小さかったので、本の結果の方が良いと思われる。

前の記事で紹介した、吃音の治癒に関して統計解析した論文
"Spontaneous" late recovery from stuttering: Dimensions of reported techniques and causal attributions
に、筆者にとって馴染みの無い統計学の用語がいくつかあったので、この機会に調べた。
この論文では主成分分析を行っているが、それらの用語は因子分析で用いられるものが多かった。

Kaiser-Meyer-Olkin (KMO) index (§2.3)

主に因子分析の文脈において、データがどれくらい因子分析に適しているかを示す指数。
データ中の各観測変数の妥当性の評価、及び分析モデルの妥当性の評価に用いられる。
MSA（Measure of Sampling Adequacy, 標本妥当性）とも言われる。

定義としては、

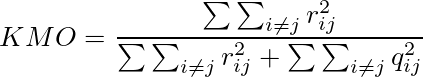
但し、

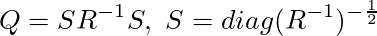
Rはデータの観測変数の相関行列
Qは偏相関行列
r_ijはRの要素
q_ijはQの要素

KMOの3つのΣΣ部分において、iについて和を取らなければ、観測変数毎の（i番目の観測変数の）KMO indexとなる。

意味としては概ね、（相関＋偏相関）中の相関の割合であり、大きいほど観測変数間に相関がある＝共通因子があるということになる。因子分析においては0.8以上が好ましく^[3]、0.5未満は"unacceptable"とされているらしい。（0.5だと相関係数と偏相関係数が同じ大きさなので共通因子無しである）

KMO indexが低い場合、変数毎のKMO indexが低い変数を除外する方法や、データ数を増やす方法があるらしい。今回の論文では、KMO indexが0.5を超えるようにデータ数を増やすという使い方がなされた。

主に因子分析の文脈で使われるが、主成分分析でデータを縮約する場合や、共通因子を見つけようとする場合にも使われるようだ。

参考文献
[1] Kaiser-Meyer-Olkin test - Wikipedia
[2] R: Kaiser-Meyer-Olkin criterion
[3] A Modernized Heuristic Approach to Robust Exploratory Factor Analysis
[4] https://htsuda.net/stats/factor-analysis.html

polychoric correlation matrix (§2.3)

ポリコリック相関係数行列。ポリコリック相関係数は、因子分析や主成分分析で順序尺度のデータを適切に扱う為に用いられるもので、順序尺度同士の相関係数を、通常の相関係数（ピアソンの積率相関係数）とは異なり、順序尺度を等間隔ではなく、正規分布に従う連続値が何段階かに分けられたものと仮定して計算される。
今回の論文では、アンケートの結果が基本的に
"definitely not true" (1),
"probably not true" (2),
"don't know" (3),
"probably true" (4),
"definitely true" (5)
の5値の順序尺度なので、それらのポリコリック相関係数に基づいて主成分分析が行われている（ポリコリック相関係数行列の固有ベクトルを主成分としていると思われる）。

参考文献
[5] 小杉先生の資料

Parallel Analysis(PA), eigenvalues > 1 criterion (§2.3 etc.)

因子分析における因子数の決定方法。
以下は代表的な因子数の決定方法の例である。

カイザー・ガットマン基準

相関行列の固有値の内、1以上のものの個数を因子数とする方法。
今回の論文に書かれている"eigenvalues > 1 criterion"はこれのことである。
1つの因子にしか負荷しない因子の固有値が最大1だから合理的である。
昔から統計ソフトが対応していたり、デフォルトの選択だったりしたので、よく使われていたらしい。
標本誤差があると因子数が多くなる傾向があり、あまり良い指標ではない。

スクリーテスト

相関行列の固有値を大きい順にプロットし、下の方が成す線から離れた大きい固有値の数を因子数とする方法。
過去にはよく使われていたらしい。

平行分析(Parallel Analysis, Horn's PA)

元のデータと同じサイズの正規乱数行列の相関行列の固有値より大きい固有値の数を因子数とする方法。
現在最も推奨される方法の1つのようだ。
今回の論文では、因子数というか、データを説明するのに有効な主成分の数（次元圧縮後の主成分の数）を決めるのに用いられている。

MAP(Minimum Average Partial)

主成分の影響を取り除いた偏相関（≒誤差の相関）の二乗和が最小になる主成分の数を因子数とするような感じの方法。

最尤解のカイ二乗検定

因子数を1から順に増やして、モデルの適合度を示すカイ二乗値が初めて有意でなくなった(p>0.05)所で止めるという方法。
因子分析のモデルを最尤法で求める場合、カイ二乗検定でモデルの適合度を調べられる。
結果がサンプルサイズによって変わるので、あまり良い指標ではないらしい。

BIC（ベイズ情報量基準）

同じく最尤解の場合に使える方法で、BICが最小になる因子数を採用する方法。
特に順序尺度のデータをポリコリック相関係数で扱う場合に合理的らしい（ポリコリック相関係数がベイズ法で計算される為。参考文献[3]より）。

参考文献
[6] 因子分析における因子数決定法（堀先生の論文）
[7] Determining the Number of Factors to Retain in an Exploratory Factor
Analysis Using Comparison Data of Known Factorial Structure
[8] R: Kaiser-Guttman Criterion

Cohen's effect size of d (§3.1)

効果量(effect size)というのは統計的仮説検定において群間の差などを表す指標で、Cohen's dやHedges' gがよく用いられる。
Cohen's dの定義は、（群1の平均 - 群2の平均）÷プールされた標本標準偏差、であり、群間の平均の差が、帰無仮説における標準偏差の何倍かを示す。
p-valueとは異なり、サンプルサイズに依存しないので、p-valueが小さすぎてわかりにくい場合などにp-valueと共に示すのが有効である。
今回の論文でも、p-valueと共に示されている。

varimax rotation with Kaiser normalization (§3.2)

バリマックス回転(varimax rotation)は、主成分（因子）の解釈性を高める為の、多次元空間における主成分（因子）軸を回転する方法の1つ。主成分（因子）の負荷量が高い変数の個数を最小化するように、主成分（因子）負荷行列の各要素を2乗したものの各列の分散が最大になるように直交回転する。
Kaiser normalizationは、バリマックス回転において、全ての変数が回転後の解に等しく影響するように、主成分（因子）負荷を正規化する。

full information maximum likelihood estimation (§3.2)

欠損データを補完する方法の1つで、変数それぞれがある分布（正規分布など）に従っていると仮定して欠損部分を最尤推定する方法。FIMLと略されるらしい。
今回の論文では、"the correlation matrix was estimated using the full information maximum likelihood estimation."と、相関係数行列の推定にFIMLが用いられるように書かれている。例えばRのpsychパッケージには相関係数行列をFIMLで計算する関数があり^[10]、内部ではFIMLにEMアルゴリズムが用いられる^[11]ようなので、欠損データをFIMLで補完してから相関行列を求めるのではなく、欠損データの補完と相関行列の推定を同時に行ったものと推測した。

参考文献
[9] FIML Basic Concepts | Real Statistics Using Excel
[10] R: Find a Full Information Maximum Likelihood (FIML) correlation...
[11] Package 'lavaan'

Mann-Whitney U test (§3.4)

2群の中央値に差があるかどうかを検定する、ノンパラメトリックな手法。
2群のデータを全て合わせて小さい方から順位をつけ、群1,群2のそれぞれの順位の和をR₁,R₂とし、U₁,U₂を
U₁ = n₁n₂ + n₁(n₁+1)/2 - R₁
U₂ = n₁n₂ + n₂(n₂+1)/2 - R₂
（n₁,n₂はそれぞれ群1,群2のデータ数）とし、その小さい方を検定量Uとし、Uの確率分布からp-valueを求めるという感じの方法。
統計検定準1級の出題範囲にもある、お馴染みのウィルコクスンの順位和検定と同じ結果になるらしい。

Benjamini-Hochberg procedure, Bonferroni correction (§3.4)

多重検定を行うと誤検出率が上がってしまう問題に対処する方法。
同じ有意水準で複数の検定を行うと、実際には有意差が無くてももどれかでは有意となる確率("familywise error rate", FWER)が上がる。例えば有意水準α=0.05とすると、実際には有意差無しでも有意となってしまう(Type I errorの)確率が0.05なので、同じ有意水準で検定を3つ行ってどれかでは有意となる確率は 1-(1-0.05)³≒0.14 となる。

Bonferroni correction（ボンフェローニ補正）は、mを検定の数として、複数の検定における有意水準を一律にα/mとする単純な方法。m個の検定のどれかが有意となる確率はαより小さくなるので、検出の基準が厳しくなる。即ち、有意なものを検出できなくなる(Type II error)確率が上がる。mが大きいほど顕著になる。

Benjamini-Hochberg procedure（BH法）は、m個のp-valueを小さい順に並べたi番目のp-valueをp_iとして、p_i≦(i/m)αを満たす最大のiまでのp_iに対応する帰無仮説を棄却するという方法。ボンフェローニ補正の問題を解消できる。

今回の論文には、年齢の違い（中央値より大か小か）、性別の違いについてMann-WhitneyのU検定で有意差があるかどうかを調べる際に、多重検定の問題はfamilywise error rateを制御するのではなくBenjamini-Hochberg procedureでp-valueを調整することで対処している、Bonferroni correctionよりは厳しくないので偽陰性の数を下げられると書かれている。

吃音治療に関する興味深い論文を入手した。
"Spontaneous" late recovery from stuttering: Dimensions of reported techniques and causal attributions
成人してから吃音が「自然に」治癒した事例について、用いたテクニックと、関係したかも知れない原因やきっかけついて統計解析をしたものである。
丁度、筆者は吃音者であり、しかも今、英語と統計学の復習をしているので、読んでみるしかないと思った。

統計関連は後にして、ここではこの論文の要約を記す。
章節毎に要約する。

■ABSTRACT
目的：
(1) 青年期以降に治療なしで吃音から回復した成人が用いたテクニックと、原因やきっかけを調査する。
(2) それらのテクニックや原因・きっかけが少数の次元にまとめられるかを調べる。
(3) それらの次元が一般的な治療方法の要素と対応しているかを調べる。

方法：
吃音から回復した124人に、49の用いられそうなテクニックと、15のあり得そうな原因・きっかけについて、当てはまるかどうかを回答してもらった。

結果：
110件のアンケート結果の主成分分析により、テクニックについては6つの成分、きっかけについては3つの成分が抽出された。

議論：
テクニックの2成分（話し方の工夫(Speech Restructuring)、雄弁術）は治療方法に対応している。別の成分（リラックス／話し方観察）は、一般的に有効と考えられている対処方法に対応している。
当事者が感じる様々な原因・きっかけからの成分は、吃音が治る要因の暗黙的な理論の差を反映している。
これらの成分の特定は、単にテクニックやきっかけをリストにしただけの従来の研究と比べて新しいものであり、今後の吃音治療の道標になるかも知れない。

■1. Introduction
吃音は幼少期には5-11%の人に見られるが、成人では0.5%（女性0.2%、男性0.8%）しか見られない。幼少期の吃音の70-80%は成長の過程で無くなる。そのほとんどは治療もせず自然に無くなるものである。
青年期に持ち越した後も自然に治ることがある。この研究は青年期以降に「自然に」治った人を対象にする。
ここでは、治ったとは吃音になったことがない人と同じくらいに完全に無くなったに限らず、感情や状況によっては出るが社会生活において支障が無い程度まで無くなったのを含む。それが実際の吃音治療の現実的なゴールとも合っている。

■1.1. Validity of self-reports on recovery
(1) その人が過去に吃音だったことと治療とは無関係に治ったことをどう確認するか？
→参考人（証人）に確認する方法が開発されている
(2) 吃音から回復した人の話し方と吃音歴の無い人の話し方は同じなのか？
→多くの場合、非流暢性が残る
(3) 吃音から回復した人は喋ることを求められるなど緊張のある状況でも出ないのか？
→回復したと主張する人の60%には吃音の傾向が残っている

■1.2. How spontaneous is a "spontaneous" late recovery?
自然に治ったという人もよく何らかの対処法を口にする。それは自分で見つけた方法とは限らない。過去に受けた治療を参考にしているかも知れない。

■1.3. What can be learned from "spontaneous" late recovery?
「自然に」治った例は治療法に示唆を与えると言われてきた。
従来の研究は定性的、今回の研究は定量的。

■1.4. Aim of the study
(1) テクニックと原因・きっかけがどれくらいあったか
(2) それらはより少ない次元にまとめられるか

■2. Method
■2.1. Participants
11歳以降に吃音が治ったという124人にアンケートした。
可能な人には参考人にもアンケートしたが、参考人が得られたのは半数以下だった。
吃音以外の言語障害だったと思われる人や、規定する程度に治ったと言えない人14人は除外した。
残った110人の年齢は14-75歳、平均44歳、吃音が始まった年齢の平均は4.8歳。
吃音治療歴は42%が治療経験なし、24%は2年以下、34%は2年以上。

■2.2. Questionnaires
吃音が治ったという人へのアンケートの質問は、その人の人物特徴、吃音が始まった年齢と終わった年齢、現在の吃音の状態、49のテクニックの内使ったもの、15の原因やきっかけの内関係したと思うもの。
これら64項目は先行研究から拾ったり、一部の著者を含む数名の過去に吃音だった人や言語聴覚士から聞き取ったもの。
各項目の選択肢は
(1) "definitely not true", (2) "probably not true", (3) "don't know", (4) "probably true", (5) "definitely true"の5値だった。

■2.3. Statistical analysis
用いられたテクニックと原因・きっかけは主成分分析を用いて次元削減した。
標本サイズが十分かどうかはKaiser-Meyer-Olkin(KMO) indexが0.5以上となることで判定した。テクニックについては0.75、原因・きっかけについては0.62だった。
アンケートの値は順序尺度の5値なので、不適切な正規分布の仮定を避ける為、polychoric correlation matrixによる主成分分析を用いた。
最適な主成分の数は、平行分析によって求めた。

■3. Results
■3.1. Validity of corroborator reports
参考人の回答は31人から得られ、その内回答が揃っていたのは20人だった。
過去の状態については、吃音特有の項目の平均が2.92(N=26)、吃音に無関係の項目の平均が1.15(N=25)であり、ｔ検定ではt=8.47、p-value<.001で有意で、吃音で間違いなさそうと確認された。
現在の状態については、吃音特有の項目の平均が1.49、その他の項目の平均が1.31であり、p-value=.092で、有意な差が無かった。
参考人の回答と吃音当事者本人の回答との相関係数は、吃音関連の項目についてはr=.46、p=.017と高くて有意であり、その他の項目についてはr=.21、p=0.32と低く、有意でなかった。

■3.2. Techniques used
49のテクニックをカイザー基準化、バリマックス回転して主成分分析し、平行分析により6つが最適とされたので6つの主成分を抽出した。
それぞれの主成分について、主成分負荷量が0.5より大きいテクニックを抜き出し、主成分負荷量×テクニックの使用率を重要度とし、重要度順に並べた（表1）。

第1主成分Aは全分散の16.2%を占めた。主な項目は「単語の最初の音を伸ばした」「音節と音節の区切りを曖昧にして繋げた」「単語の終わりと次の単語の始まりを繋げた」「単語のアクセントを変えた」「深い声で話した」「リズムよく話した」なので、この成分を「話し方の工夫」とラベル付けした。

第2主成分Bは全分散の15.1%を占めた。主な項目は「できるだけリラックスに努めた」「話の区切りを十分に取るよう気を付けた」「何をどのように話すかを考える時間をより長くした」「常に自分の話し方、言い方に集中するようにした」「話す間のリラックスした呼吸に集中するようにした」「話すテンポを下げた」なので、この成分を「リラックス／話し方観察」とラベル付けした。

第3主成分Cは全分散の10.9%を占めた。主な項目は「大きな声で読むか、誰かの前で読む」「問題のあった音や単語を分析した」「詩を読んだ」「非吃音者と一緒に大きな声で朗読した」「鏡の前で自分自身に話した」であり、この成分を「雄弁術」とラベル付けした。

第4主成分Dは全分散の7.5%を占めた。主な項目は「歌のレッスンを受けた」「演劇のレッスンを受けた」であり、この成分を「演劇」とラベル付けした。

第5主成分Eは全分散の7.1%を占めた。主な項目は「公衆の前でスピーチをした」「議論に積極的に参加した」「敢えて困難な話す場に参加した」であり、この成分を「話す必要性の探求」とラベル付けした。

第6主成分Fは全分散の6.9%を占めた。主な項目は「話し始めを楽にする為に直前にアイコンタクトした」「特に吃音が出た時や予期した時にアイコンタクトを維持するよう努めた」であり、「安心感の確保」とラベル付けした。

この6主成分で全分散の63.7%が説明される。他の8主成分は固有値>1になり得たが、平行分析により無視された。

表1. 非流暢さの低減の為に使ったテクニック、使った人の割合、主成分負荷量、重要度（割合×負荷量）

Technique used（用いたテクニック）	%	Loading	Importance
Component A: Speech Restructuring（話し方の工夫）
Stretched out the beginnings of words 単語の最初の音を伸ばした	22	.72	15.8
Slurred speech gliding smoothly from syllable to syllable 音節と音節の区切りを曖昧にして繋げた	21	.68	14.3
Connected the end of a word with the beginning of the next one 単語の終わりと次の単語の始まりを繋げた	20	.68	14.3
Changed word accent 単語のアクセントを変えた	18	.71	12.8
Spoke with a deeper voice 深い声で話した	13	.78	10.1
Spoke rhythmically without an external pacemaker メトロノームとか無しでリズムよく話した	13	.56	7.3
Spoke with a higher voice 高い声で話した	7	.80	5.6
Controlled lip muscles such that lips did not touch each other 唇がくっつかないよう唇の筋肉を動かした	10	.51	5.1
Sung utterances (rap, parlando) 歌うように話した（ラップのように）	8	.56	4.5
Reduced perception of own voice by speaking with masking noise マスクノイズを使って自分の声が聞こえにくくした	6	.74	4.4
Took relaxing or other anti-stuttering medication 緊張を緩和する薬を使った	5	.76	3.8
Spoke with an external pacemaker (e.g. metronome) メトロノームとかを使ってリズムよく話した	5	.62	3.1
Component B: Relaxed/Monitored Speech（リラックス／話し方観察）
Tried to be more relaxed at all できるだけリラックスに努めた	40	.72	28.8
Took care to make enough speech breaks 話の区切りを十分に取るよう気を付けた	38	.74	28.1
Took more time for thinking beforehand what to say and how to say it 何をどのように話すかを考える時間をより長くした	33	.79	26.1
Always tried to concentrate on my speaking manner 常に自分の話し方、言い方に集中するようにした	33	.76	25.1
Concentrated on even and relaxed breathing while speaking 話す間のリラックスした呼吸に集中するようにした	37	.67	24.8
Reduced speech tempo 話すテンポを下げた	33	.65	21.5
Concentrated on what I will say, not how I will say it どう話すかでなく何を話すかに集中した	29	.70	20.3
First thought, then spoke 考えてから話すようにした	33	.56	18.5
Took a deep breath before each utterance 都度発声前に深呼吸した	22	.64	14.1
Tried to speak clearly with precise articulation 正確な発音で明瞭に話すよう努めた	22	.63	13.9
Relaxed before certain utterances and spoke as soon as I was relaxed 吃る音の発声前にリラックスし、リラックスできたら直ちに発声した	20	.58	11.6
Component C: Elocution（雄弁術）
Read aloud or to someone 大きな声で読むか、誰かの前で読む	29	.63	18.3
Analyzed sounds and words with which I had problems 問題のあった音や単語を分析した	25	.64	16.0
Analyzed what my articulatory muscles did during stuttering 吃った時の発声器官の筋肉の動きを分析した	18	.68	12.2
Read poems 詩を読んだ	15	.76	11.4
Worked on my secondary symptoms (e.g. tics, arm movements, grimaces) 二次的な症状に対処した（ゆすり、腕の動き、しかめっ面など）	14	.59	8.3
Read texts aloud together with a fluent speaker 非吃音者と一緒に大きな声で朗読した	12	.66	7.9
Talked to myself in front of a mirror 鏡の前で自分自身に話した	10	.63	6.3
Purposely used difficult words わざと言いにくい単語を選んだ	12	.52	6.2
Component D: Stage Performance（演劇）
Took singing lessons 歌のレッスンを受けた	10	.74	7.4
Took acting lessons 演劇のレッスンを受けた	7	.74	5.2
Learned to play a wind instrument 吹奏楽器の演奏を学んだ	2	.88	1.8
Component E: Sought Speech Demands（話す必要性の探求）
Held public speeches 公衆の前でスピーチをした	25	.89	22.3
Participated actively in discussions 議論に積極的に参加した	34	.63	21.4
Participated purposely in difficult speech situations 敢えて困難な話す場に参加した	20	.79	15.8
Component F: Reassurance（安心感の確保）
Made eye contact seconds before speaking in order to ease speech onset 話し始めを楽にする為に直前にアイコンタクトした	24	.71	17.0
Tried to keep eye contact, especially when I stuttered or expected to 特に吃音が出た時や予期した時にアイコンタクトを維持するよう努めた	26	.59	15.3
Paid heed to a stress-free life with sufficient sleep and physical activity 十分な休息と運動でストレスの少ない生活を心掛けた	23	.65	15.0
Items not loading sufficiently on any main component（どの主成分にも十分な関係が無いもの）
Stopped when I stuttered a word and repeated it 吃ったら一度止まって繰り返した	30
Sought out relaxed speech situations リラックスして話せる場を探した	28
Spoke with soft voice onset 出だしは優しく発声した	24
Quit avoiding or replacing difficult words 言いにくい言葉を避けたり言い換えたりするのをやめる	23
Increased voice volume (e.g. through deep breathing) 呼吸を深くして声を大きくした	19
Consciously relaxed parts of my speech apparatus 発声器官の部位を意識的にリラックスさせた	16
Used relaxation exercises リラックスする為の訓練法を使った	15
Stuttered purposely but differently than usual わざと普段と異なる吃り方をした	11
Participated in rhetoric courses 雄弁術の講座に参加した	9

■3.3. Causal attributions for the recovery
15の原因やきっかけについて、同様に主成分分析を行い、3つの主成分を抽出した。（表2）

第1主成分(I)は全分散の24.1%を占めた。主な項目は「新しい職場で仕事を始めた」「学校を卒業した」「住居を変えた」「新しいパートナーに巡り合った」「違う言語の国に移住した」なので、この成分を「生活の変化」とラベル付けした。

第2主成分(II)は全分散の17.9%を占めた。主な項目は「自信が増した」「自分の話し方を否定的に捉えなくなった」「自分の吃音に対する他人の反応が気にならなくなった」「自分が吃音者だと思わなくなった」なので、この成分を「姿勢の変化」とラベル付けした。

第3主成分(III)は全分散の16.0%を占めた。主な項目は「大事な人に動機づけられた」「自分の吃音について何か変えようと決心した」「大事な人に吃音に取り組んでいることを伝えた」「心理学者や心理療法士の指導を受けた」なので、この成分を「社会的支援」とラベル付けした。

表2. 非流暢さの低減に繋がった原因やきっかけ、該当する人の割合、主成分負荷量、重要度（割合×負荷量）

Reason or occasion to which disfluency reduction was attributed（非流暢さの低減に繋がった原因やきっかけ）	%	Loading	Importance
Component I: Life Change（生活の変化）
I started at a new workplace 新しい職場で仕事を始めた	18	.82	14.8
I finished school 学校を卒業した	18	.82	14.8
I met a new partner 新しいパートナーに巡り合った	12	.80	9.6
I changed my residence 住居を変えた	11	.90	9.9
I moved into a country with another language 違う言語の国に移住した	5	.78	3.9
Component II: Attribute Change（姿勢の変化）
My self-confidence increased 自信が増した	56	.63	35.3
I did not evaluate my speech negatively any longer 自分の話し方を否定的に捉えなくなった	28	.82	23.0
I became insensitive about reactions by others to my stuttering 自分の吃音に対する他人の反応が気にならなくなった	22	.75	16.5
I no longer accepted that I was one who stuttered 自分が吃音者だと思わなくなった	22	.67	14.7
Component III: Social Support（社会的支援）
I decided to change something about my stuttering 自分の吃音について何か変えようと決心した	35	.53	18.6
I was motivated by persons who were important to me 大事な人に動機づけられた	29	.83	24.1
I told a person important to me that I was working on my stuttering 大事な人に吃音に取り組んでいることを伝えた	15	.85	12.8
I had counseling by a psychologist/psychotherapist 心理学者や心理療法士の指導を受けた	8	.68	5.4
Items not loading sufficiently on any main component（どの主成分にも十分な関係が無いもの）
I decided to treat my stuttering my own way 自己流で吃音を直すと決めた	40
I accepted the fact that I was one who stuttered 自分が吃音者であることを受け入れた	33

■3.4. Age and gender effects
年齢の違い（中央値より大か小か）、性別の違いについて、Mann-WhitneyのU検定で確認した結果、どの項目についても有意な差は無かった。
ただ1項目、年齢が高い層には、「自分の吃音に対する他人の反応が気にならなくなった」が多かった。

■4. Discussion
■4.1. Comparison with previous findings
従来の研究と比較する。
話す速度を下げること、話し方を変えること、は従来の研究同様、よく使われていた。
リラックスは従来の研究とは異なり、よく使われていた。
雄弁術や話すことを求められる場の追求は、今回の調査では比較的多かったが、従来の研究では特筆されなかった。

原因やきっかけについては、従来の研究と同様、自信の向上が一番であり、話し方を変えたい欲求も多かった。生活環境の変化は、割合としてはさほど多くは無いものの、従来の研究では特筆されなかったものである。

加えて、今回の研究では、アルゴリズム的に項目をグループ化したので、類似の、同時に使われやすいテクニックや、暗黙的な回復の要因を示す類似の項目が得られた。

■4.2. Do the components mirror stuttering treatments?
今回検出した、成人後に「自然に」治った事例の主成分は、成功している吃音治療と類似があるか、治療法に示唆があるか、という問いに対しては、2つの理由で、あると考える。
(1) 既存の治療方法は、理論や実証だけではなく、吃音者の肯定的な経験にも基づくから。
(2) 成人してからの回復は本当に「自然」に回復したとは限らない。いくらかは、過去の治療や、その他の情報源から得た既存の治療法を参考にしたと考えるべきである。

第1主成分の「話し方の工夫」は、単語の始まりを伸ばすなど、吃音治療で使われる方法で主に構成されている。
第3主成分の「雄弁術」は、20世紀半ばまで一般的な治療法だった。
第2主成分の「リラックス／話し方観察」は正式な治療法を反映しているようには見えないが、自身で行う方法としては一般的であり、治った本人の感覚としては効果があった要因として挙げられることが最も多いという報告もある。

原因やきっかけについて検出した3つの主成分に関しては、いずれも治療法に繋がり得るものであるし、自分や自分の話し方の「姿勢の変化」は吃音からの回復の主要因の1つとして報告されたことがある。

■4.3. Attribution biases
テクニックは実際に用いたからそれほど当てはまらないが、主観的な原因やきっかけはいくつかのバイアスがあり、額面通りに受け入れられないので注意が必要。
(1) 吃音が治ったというような通常でない作用は、同時期に起こったイベントを原因にされやすい。
(2) 原因やきっかけは事後に言っているものであり、よくわからないものを説明できるように、認知的不協和を減らせるように考えられやすい。
(3) 原因やきっかけは自分をひいきしやすい。成功の要因は自分の中に求め、失敗の要因は外部に求めやすい。

■4.4. Validation of former stuttering of the participants
吃音から回復したという自己申告はどこまで信用できるかについては、参考人の回答から、過去の吃音に関する回答の平均値と現在の吃音に関する回答の平均値の差の効果量が3σに相当するくらい大きいことから明確に説明される。

■4.5. Strengths and limitations of the study
この研究は主成分分析という主観的でない手法を使っていることに意味があり、従来の研究を否定するものではなく補強するものである。
1つの限界として、吃音が治ったの程度の問題がある。例えば「現在吃音の傾向がある」に「滅多にない」と回答した62人中26人は「緊張やプレッシャーがある時には吃る」に「時々ある」と回答した。従って、過去に吃音があった人は、状況によっては吃る程度なら治ったと考えている。
もう1つの限界として、「自然に」治ったの意味がある。人は情報や事実を覚えていても情報源を覚えていない傾向があることが知られている。回答者の52%は過去6ヶ月以上前に吃音治療を受けたことがあると回答している。過去の治療の影響は除外できない。
もう1の限界として、言語療法士による参加者の吃音の診断結果が無いことがある。ただ、(1)58%の人は言語療法士による治療を受けたこと、(2)信頼できる手法を使って過去の吃音を調べたこと、(3)参加者は吃音の専門家や自助組織を経由して集められたこと、からして参加者が過去に吃音が無かった人だとは考えられない。

■4.6. Conclusion and future directions
この研究で報告した吃音から回復した人が使ったテクニックや原因・きっかけは、吃音が、感覚運動系、社会性、動機、神経系に関連し、症状が状況、感情、注意、言語学的な要因に依存する、複雑な障害であるという現在の理解と合う。
今回統計学的な手法で抽出した次元は、現在の吃音治療の改良にも役立ち得る。(1)「話し方の工夫」「雄弁術」は現在の、そして驚くべきことに過去の吃音治療の構成要素に対応する。(2)「リラックス／話し方観察」は専門的ではないが一般に有効と考えられている吃音への対処法であり、吃音治療に取り入れられる可能性がある。(3)原因やきっかけの要素は、素人理論を反映しており、吃音治療で利用できる可能性がある。
今回の調査結果は吃音の脳画像解析にも示唆を与える可能性がある。最近の研究で、吃音が「自然に」治ったという人と流暢性形成法の治療を受けた吃音者の治療前後のfMRI画像を比較したものがあり、「自然に」治ったという人は脳神経回路における発話時の異常に対応する部位の挙動が独立だったとしている。これが「自然に」治ったことを示すものなら、今回の調査結果に注目した吃音治療によって同様の脳画像が得られることが示せるかも知れない。