フィボナッチ数列の任意の項を高速に計算する方法

そんなプログラミングの問題を見かけて、反射的に思ったのは、一般項を用いることだった。
フィボナッチ数列の漸化式はa_n=a_n-1+a_n-2なので、一般項a_nを求めることは可能である。

3項を含む漸化式は、特性方程式を用いて解くのが基本であるが、やり方を忘れてしまったので、自己流で解いてみた。
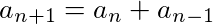
$a_{n+1} = a_{n} + a_{n-1}$
を
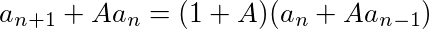
$a_{n+1} + Aa_n = (1+A)(a_n+ Aa_{n-1})$
という形にできると、
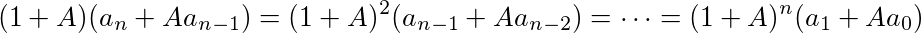
$(1+A)(a_n+ Aa_{n-1}) = (1+A)^2 (a_{n-1}+ Aa_{n-2}) = \cdots = (1+A)^n(a_1+Aa_0)$
であることと、a₁=1, a₀=0であることを用いて
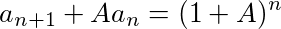
$a_{n+1} + Aa_n = (1+A)^n$
とできる。このAは、a_n-1の係数を見ると、(1+A)A=1となるAなので、A=(-1±√5)/2である。従って、
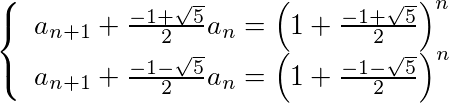
$\left\{ \begin{array}{c} a_{n+1} + \frac{-1+\sqrt{5}}{2} a_n = \left(1 + \frac{-1+\sqrt{5}}{2}\right)^n \\ a_{n+1} + \frac{-1-\sqrt{5}}{2} a_n = \left(1 + \frac{-1-\sqrt{5}}{2}\right)^n \end{array} \right.$
であり、上の式から下の式を引いて整理すると、
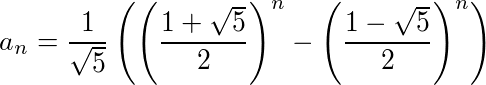$a_n = \frac{1}{\sqrt{5}} \left( \left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n \right)$ と求まる。
念の為申し上げるが、このa_nはnが何であろうとも整数である。実にミラクルである。

√5のn乗なんてのがあるのでは、誤差が出まくるだろうとは思ったが、CやJavaでは浮動小数点の精度が低くて無理でも、PythonのmathパッケージにMathematicaやMaxima並の驚異の性能が無いとは限らないので、試しに

#!/usr/bin/python
from math import pow
from math import sqrt

def fib(n):
    return int(1/sqrt(5)*(pow((1+sqrt(5))/2,n)-pow((1-sqrt(5))/2,n)))

an_2 = 0  #a_{n-2}
an_1 = 0  #a_{n-1}
an = 1    #a_{n}
for i in range(1, 100):
    print "n =", i, "a_n =", an, "fib(n) =", fib(i)
    if fib(i) != an:
        print "error!"
    an_2 = an_1
    an_1 = an
    an = an_1 + an_2

とやってみた所、72項目で誤差が出た。
Maximaはn>200000でも正確な整数を弾き出す（下記入出力参照、下3桁が正しいことを確認）が、さすがにPythonでは無理だった。おそらく、Maximaは内部で√5を√5として保存しながら数式処理をしてるからであろう。Pythonの言語仕様上、pow()の結果は一度float値にしないといけないので、正確な整数値を出すには無限の精度が必要になってしまう。

Maximaへの入力とその出力

(%i1) 1/sqrt(5)*(((1+sqrt(5))/2)^n-((1-sqrt(5))/2)^n),n=234567,ratsimp;
(%o1) 179607932890115544888825400217[48962 digits]014673023583001136817746498978

MathematicaやMaximaを使って良いなら、一般項を用いる方法もあるが、今回の問題は、「複数言語選択可能」としながら、MathematicaもMaximaも選択肢に無かった。フィボナッチ数列のn項目を高速に計算する方法は、他には思い付かなかったのだが、少し調べると、計算量がO(log N)になる簡単な方法があった。

$M=\pmatrix{1 & 1 \cr 1 & 0}$ とすると、M^n-1の{1,1}要素がフィボナッチ数列のn項目だというのが使える。
さらに、M=M*Mという計算を繰り返すことにより、M^(2^k)は計算量少なく求められるので、M^n-1をM^(2^k)の積とすることによって、高速に計算できる。
例えば、
M⁵ = 0*M⁸ · 1*M⁴ · 0*M² · 1*M
M¹⁰ = 1*M⁸ · 0*M⁴ · 1*M² · 0*M
であるように、2進数にした時の1のビットに対応するM^(2^k)を掛け合わせれば良いのである。

従って、例えば次のようにすれば、n=10000でも高速に計算される。（Pythonで扱える整数の上限はメモリが許す限り無限である）

#!/usr/bin/python

class multipliable_2x2matrix(object):
    def __init__(self, a, b, c, d):
        self.a = a;
        self.b = b;
        self.c = c;
        self.d = d;
    def mul(self, b):
        return multipliable_2x2matrix(
            self.a * b.a + self.b * b.c,
            self.a * b.b + self.b * b.d,
            self.c * b.a + self.d * b.c,
            self.c * b.b + self.d * b.d)
    
def fib(n):
    if n == 0: return 0
    m = multipliable_2x2matrix(1, 1, 1, 0)
    f = multipliable_2x2matrix(1, 0, 0, 1)
    n = n - 1
    while n > 0:
        if n & 1 == 1:
            f = f.mul(m)
        n = n >> 1
        m = m.mul(m)
    return f.a

Weblog on mebius.tokaichiba.jp

フィボナッチ数列の任意の項を高速に計算する方法

コメント