[OpenGL] 平面への投影変換で影を付けてみる

OpenGLでオブジェクトに影を付けようとして、最初に思い付いた方法は、地面に投影する変換行列を作って、同じオブジェクトを黒で描画することだったが、それが意外と難しかった。

そこで調べてみたが、オブジェクトへの影の付け方には色々な方法があるようで、影オブジェクトを別に作成する方法を除くと、大体次の３通りが多いようだ。
・変換行列による平面への投影
・シャドウボリューム法
・シャドウマッピング法
正確に説明できる自信が無いので、説明は省く。とりあえずわかったのは、簡単に実装できる方法は無いということだった。
平面上にできる影であれば、やはり行列による投影変換で描画するのが最も簡単なので、引き続き、納得できるまで取り組むことにした。

・結果
object drawn with shadowobject drawn with shadowobject drawn with shadow
・ソースコード

光源の位置をL:(Lx,Ly,Lz,1)とすると、任意の3次元座標を、法線(a,b,c)が光源側を向く平面ax+by+cz+d=0に投影する行列は、次のような行列であることは、色々な所に書かれている。
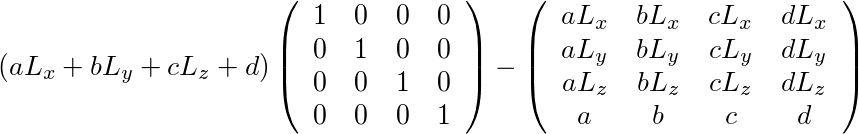
shadow matrix
一応、これを筆者なりに求めてみる。

L=(Lx Ly Lz Lw)T : 光源
P=(x y z 1)T : 物体の位置
P'=(x' y' z' 1)T : 平面 ax+by+cz+d=0 に投影されたPの位置
N=(a b c d)T : 平面のパラメーター、但しNT L > 0（法線(a,b,c)が光源側を向くことより）

とし、P' = M P を満たす行列 M を求めることを考える。
P'はLとPを含む直線上にあるので、スカラー媒介変数 t を用いて
P' = L + t(P-L) --- (1)
と表せる。P'は平面上にあるので、
NTP' = 0
成り立つ。これより、
NT P' = NT L + t NT (P-L) = 0
なので、t = - NTL / (NT(P-L)) とわかる。NTL > 0なので、
t = NT L / (NT(L-P))
としておく。このtを(1)に代入し、両辺をNT(L-P)倍すると、
NT(L-P) P' = NT(L-P)L + NTLP - NTLL
= NTL P - NTP L
= NTL P - L NTP ※（NTPはスカラーなのでこのように入替可能）
= (NTL - LNT) P
となる。ここで、P'の4つ目の要素をscale factorだとすると、P'とそれをスカラーk倍したk P'は同じ位置を表すので、P'とNT(L-P) P'も同じ位置を表している。従って、Mは NT(L-P) P' = M P を満たすMでも良いので、Iを単位行列として
M = (NTL I - LNT)、つまり
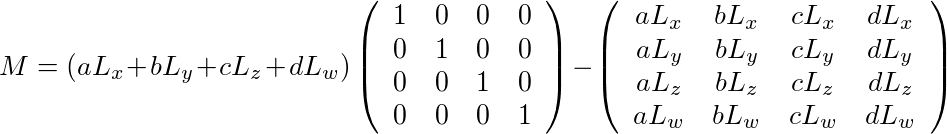
shadow matrix
と求まる。


この行列をmodel view matrixに掛け合わせて、描画した地面に重ねて影を描画すると、影にノイズが出たり、全く影が表示されなかったりすることがある。
object drawn with shadow
少しでも影を浮かせると正常に表示されるが、全く同じ位置に重ね書きしようとすると、depth値の丸め誤差の都合で、所々に地面より向こうだと判断されてしまうフラグメントが発生するのが原因である。（Zテストで落とされるので、ブレンディング描画にしても解決しない。）
地面と全てのオブジェクトの影を先に描くことが可能なら、depth testを無効化して影を描画することも考えられるが、こういう時はpolygon offsetを設定するのがOpenGLの定跡であるので、今回もそのようにした。

glPolygonOffset(-1, -1);
glEnable(GL_POLYGON_OFFSET_FILL);
PolygonOffset()の引数の意味は難解なのだが、大抵の場合、少し向こう側ということにするなら(+1,+1)、少し手前ということにするなら(-1,-1)とすれば良いとされている。
このソースコードでは、手前に見える（地面に隠されない）はずの影を描画するための設定なので、(-1,-1)としているが、逆に地面に対してPolygonOffset(+1,+1)としても良い。


影を真っ黒で描画してしまうと、環境光で多少は照らされるはずの地面が全く見えなくなって不自然なので、影は半透明の黒で、つまり多少は地面が透けて見えるように描画したい。
その為には、αブレンディング描画をすれば良い。

glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
これだけでオーソドックスなαブレンディングが有効になる。


影をαブレンディング描画をすると、平面に投影したポリゴンが重なると、影が2重になってしまう。
object drawn with shadow
このオブジェクトはいくつかのパーツを重ねて描画しているので、パーツ毎の影が重なるとこのようになる。
物体が半透明でない限りは、これは不自然である。これを防ぐには、ステンシルバッファを使うのが最善だと思う。
OpenGLのステンシルはマスクのような役割をし、ステンシルテストをパスしたフラグメント（viewport上のピクセル）を描画しながら、描画した位置のステンシル値を更新することができる。
例えば、このようにする。

glEnable(GL_STENCIL_TEST);
glClear(GL_STENCIL_BUFFER_BIT);
glStencilFunc(GL_NOTEQUAL, 1, 1);
glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);
描画をステンシル値が0のピクセルに限りながら、描画したピクセルのステンシル値を1に置き換えることにより、どのピクセルも2回描かれないようにするものである。


無限に広がる平面でなく、有限の地面を描画する場合、影が地面をはみ出すと不自然である。影が地面をはみ出さないようにするには、地面が四角形であればOpenGLのclip planeを無理矢理使う方法も考えられるが、今回はこれもステンシルテストで解決した。

glEnable(GL_STENCIL_TEST);
glClear(GL_STENCIL_BUFFER_BIT);
glStencilFunc(GL_ALWAYS, 1, 1);
glStencilOp(GL_KEEP, GL_KEEP, GL_REPLACE);
/* 地面の描画 */

glStencilFunc(GL_EQUAL, 1, ~0);
glStencilOp(GL_KEEP, GL_KEEP, GL_INCR);
/* 影の描画 */
glDisable(GL_STENCIL_TEST);

地面を描く時にステンシル値を1に置換し、影の描画をステンシル値が1のピクセルに限りながら、影を描画したピクセルのステンシル値を+1することにより、地面がある場所のみ描画するのと影が2重に描かれないのを実現している。


なお、影を描画する際にはdepth maskによってdepth bufferへの書き込みを停止するのが、OpenGLにおける影描画の定跡である。

glDepthMask(GL_FALSE);
これによって、depth buffer上で影の位置が地面より少し盛り上がるのを避けることができる。
そのためにも、上記のpolygon offsetの件は、地面をPolygonOffset(+1,+1)して描画するより、影をPolygonOffset(-1,-1)して描画する方が適切だと思う。

なお、ステンシルバッファが有効でないと、
glEnable(GL_STENCIL_TEST);
としてもステンシルテストが有効にならず、OpenGLの仕様により、テストが常にpassしたことになり、全てのフラグメントが描画されてしまう。GLUTでステンシルバッファを有効にするには、例えば次のようにする。
glutInitDisplayMode(GLUT_RGBA | GLUT_DOUBLE | GLUT_DEPTH | GLUT_STENCIL);


サンプルコードでは、影の色はlighting有効でmaterialの設定によって付けるようにしているが、これは今回のモジュール構成上こうするのが楽にオブジェクトの色を黒にできたからで、あまり意味が無い。計算量ためにも、lightingを無効にして、glColor4f()等で着色するべきだろうと思う。
Textureによる着色のみなら、vertex arrayに関係なくglDisable(GL_TEXTURE_2D);とすれば無効にできるのだが、今回は、color materialによってオブジェクトに着色する都合で、vertex arrayのcolor arrayを有効にしているので、glColor4f()等で着色するには、lightingを無効にする他に、BindVertexArray()した後にcolor arrayを無効化する必要があり、面倒なのである。

Color materialを有効にすると、1つの頂点配列の中でもポリゴン単位でdiffuse colorを変えることができるので、テクスチャーを使わなくてもカラーオブジェクトをライティング有効で描画できて便利だと思って使ってみた。


ところで、このページに、平面への投影行列の求め方がとても簡潔に書かれているが、いつの間にかXsがスカラー倍されているのが、筆者としては納得できない。t+u=1の縛りが抜けているのに、結局t=u=0の解を排除するだけで求まっているので、何というか、たまたま求まっている感じがする。

ところで、筆者のMacでは、ステンシルテストを有効にしているのに、たまに影が2重に描画されてしまうことがある。（下図赤丸内）
object drawn with shadow
光源が地面に近くて影が長い時に起こりやすい。FreeBSD+Mesaのソフトレンダリング環境では起こらないので、Mac特有の問題のような気がするが、それにしても不思議である。