SVGで半透明図形の外側にドロップシャドーを付けるには？

暫くこのweblogを更新してないので、リハビリの為に何か書く。
これまで、代わりにTwitterとかをやってた訳ではなく、weblogとかを書きたく無くなった訳でもなく、ネタはあって細かいことは色々やってはいたのだが、何をやっても成果が出ないのである。考え事のネタだけが溜まっていく。物書き用のMacBookが不調で筆無精になってたり、部屋の地デジ化に時間を奪われたり、肺炎に罹ったりしたこともあったが、土日もクタクタで、そもそも頭を使うことに取り組む時間が激減してるので、トシなのだろう。

話を戻して、SVGでドロップシャドーを付けるには、SVG 1.1のドキュメントの§15.1のサンプルコードのように、feGaussianBlurを使ってぼかしてずらしたものを先に描けば良いのだが、影を付ける対象が半透明だと、半透明の部分に自身の影が透けて暗くなってしまう。例えば、この方法で
dropshadow0.svg（注：この画像はJPEG、クリックするとSVGファイルが開きます）
この四角の上にある半透明の円に影を付けると、
dropshadow1.svg（注：リンク先はSVGのfilterに対応していないブラウザでは影が出ません）
このように、円の内側が暗くなってしまう。もし、円の外側にだけ影を付けたい場合、どうすれば良いだろうか。
手前に光源があれば、円の内側の半透明部分も影を作り出すんだから、円の内側に影が入り込むのは当たり前だろ、と言われればその通りである。この所、ブログの記事を書き始めてから問題設定に問題があることに気付いて、草稿をボツにすることが度々発生するのだが、今日はこのまま書き続ける。

上のSVGでは、SVG 1.1のドキュメントのサンプルコードに従って、

<filter id="dropShadow1" width="150%" height="150%">
<feGaussianBlur in="SourceAlpha" result="blur" stdDeviation="5"/>
<feOffset in="blur" result="offsetBlur" dx="10" dy="10"/>
<feBlend in="SourceGraphic" in2="offsetBlur" mode="normal"/>
</filter>
このようなフィルターを定義しており、元の絵(SourceGraphic)と影との合成にfeBlendを使っているが、これをfeMergeに替えて
<filter id="dropShadow1" width="150%" height="150%">
<feGaussianBlur in="SourceAlpha" result="blur" stdDeviation="5"/>
<feOffset in="blur" result="offsetBlur" dx="10" dy="10"/>
<feMerge>
<feMergeNode/> <!-- blurred and offset image -->
<feMergeNode in="SourceGraphic"/>
</feMerge>
</filter>
にしても結果は同じである（feMergeはnormalモードでfeBlendするのと同じ）。

SVGでは、オブジェクトにα値がある限り、オブジェクトの重ね合わせにはα合成が発生するので、下の絵を消すかのようにα値ごと上書きすることはできない。<filter>〜<filter>の中では、feBlendやfeComposite等を使うことによりブレンドモードを変えることができ、特に<feComposite operator="arithmetic" k1="0" k2="0" k3="1" k4="0" />とすると重ねる絵で完全に上書きすることができるが、これらは矩形でしか行えないので、重ねる絵の何も無い部分（α=0のピクセル）も上書きして、下の絵を消してしまう。従って、

<filter id="shadow_normal" width="150%" height="150%">
<feGaussianBlur in="SourceAlpha" result="blur" stdDeviation="5"/>
<feOffset in="blur" result="offsetBlur" dx="10" dy="10"/>
</filter>
これによってできる
dropshadow2.svg
こういう影の画像に元の絵を重ねるのではなくて、
dropshadow3.svg
こういう影の画像を作らないといけない。このdropshadow3.svgでは
<filter id="shadow_out" width="150%" height="150%">
<feGaussianBlur in="SourceAlpha" result="blur" stdDeviation="5"/>
<feOffset in="blur" result="offsetBlur" dx="10" dy="10"/>
<feComposite in="SourceAlpha" in2="offsetBlur" operator="arithmetic"
k1="0" k2="-100" k3="1" k4="0" />
</filter>
のようにして、元の画像のα値を-100倍して重ねることにより、元の画像のα > 0.01の部分のαを0にしている。これで目的が達成できているように見えるが、元の画像を重ねると
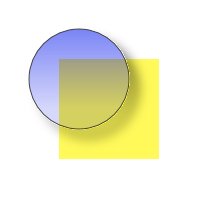dropshadow4.svg
このように、少し隙間ができてしまう。これは、元の画像の輪郭の、輪郭を外れた少し外側に、アンチエイリアシングによって生じる微小なαを持つピクセルがあるからだと考えられる。上の例では右下に影を付けているので、影を左上にずらせば隙間を隠せるのではないかとも思うが、
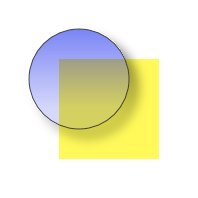dropshadow5.svg
この円の右上のように、隙間は右下にできるとは限らない。

次に、フィルターではなくクリップやマスクを使って影をカットすることを考える。まず問題になるのは、<clipPath>によって作られるクリッピング領域はパスの内側を残すクリップだということである。SVGではクリップやマスクを反転させる術は無いように思える。パスの外側を塗り潰すことが難しいのと同様に、パスの外側を残すクリップを作るのも難しいのである。
しかし、clip-ruleにevenoddを指定することによって穴開き領域を作ることができることを利用して、十分に大きな領域の内側に消したい領域の穴を開けたクリップを作ることは可能である。
そう思って、

<clipPath id="does_not_work" clip-rule="evenodd">
<rect x="0" y="0" width="200" height="200"/> <!-- 十分大きな領域 -->
<circle cx="80" cy="80" r="50"/> <!-- 消したい部分 -->
</clipPath>
のようにしてクリッピング領域を作ってみたが、これはrect部分からcircle部分が抜き取られるのではなく、rect部分とcircle部分の和になってしまった。evenoddは１つのパスで完結しないと働かないようである。
そこで、上記のrectとcircleをpathに置き換えて連結してみた。
<clipPath id="shadow_clip" clip-rule="evenodd">
<path d="M0,0 H200 V200 H0 V0
M130,80
C130,107.6 107.6,130 80,130
C52.4,130 30,107.6 30,80
C30,52.4 52.4,30 80,30
C107.6,30 130,52.4 130,80
Z"
/>
</clipPath>
これによって影を切り取ると
dropshadow6.svg
このようになり、元の絵を重ねると、
dropshadow7.svg
となり、所望の外側だけのドロップシャドーが得られた。

とりあえず目的は達成できたが、問題点として、
(1) SVGファイル内に似たようなパスデータが何度も現れる
(2) 影をつける対象は必ず１つのパスで書けなければならない
がある。(1)は似たようなパスでクリップと影と本体を別々に書かないといけないことによる。影と本体は、次のdropshadow8.svgのようにxlinkとuseを使ってパスを共通化できるが、クリップとの共通化は難しい。(2)とも共通する課題だが、複数のパスデータをclip-rule="evenodd"が利くように繋げる手段や、複数の要素をclip-rule="evenodd"で並べる手段が見つからないのが原因である。
dropshadow8.svg（xlinkを使って少しまとめたもの）

やはり問題設定が適切でないということだろうか。

ところで、上記の<circle>タグと置き換えたパスは、たった4つのCUBIC_TOセグメント（3次ベジエ曲線）で近似しているにしては、円として全く違和感が無い。次の図は<circle>による円を太い赤で重ねたものだが、黒い円が見事に収まっている。
dropshadow9.svg
筆者はInkscapeというフリーのドローイングソフトの円をパスに変換する機能で知ったのだが、単位円の(1,0)から(0,1)までの弧は、(1,0),(1,0.5523),(0.5523,1),(0,1)という4点のベジエ曲線で近似できるのである。

この0.05523というのはどこから出てくるのかと気になったので、調べてみた。
(Xi,Yi)をi番目の制御点とすると、n次ベジエ曲線の式は、0≤t≤1の媒介変数tを使って、
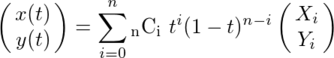
\pmatrix{x(t) \cr y(t)}=\sum_{i=0}^{n} {\mathrm _nC_i} \ t^i (1-t)^{n-i} \pmatrix{X_i \cr Y_i}
と表されるので、3次ベジエ曲線は

x(t) = (1-t)3X0 + 3t(1-t)2X1 + 3t2(1-t)X2 + t3X3

y(t) = (1-t)3Y0 + 3t(1-t)2Y1 + 3t2(1-t)Y2 + t3Y3

である。これの(X0,Y0)〜(X3,Y3)を調節して1/4円に近似することを考える。(1,0)から(0,1)までの1/4円の場合、X0=1, X3=0である。X座標についてあと2つ条件を与えればX1,X2が決まるので、t=0.5の時に円弧の中点(cos π/4, sin π/4)を通ることと、t=0の点のxの微分が0であることを使う。
x'(t)=-3(1-t)2+(3-6t+9t2)X1+(6t-9t2)X2
にt=0を代入すると、x'(0)=-3+3X1=0となるから、X1=1が得られ、
x(1/2)=(1/2)3+3(1/2)3+3(1/2)3X2=√2/2
の両辺を8倍すると4+3X2=4√2だから、X2=(4√2 - 1)/3≒0.5523となる。XiとY3-iは対称なので、Y1=X2, Y2=X1であり、(X0,Y0)〜(X3,Y3)は上記の4点となる。

といっても、たった3点を円に合わせただけのパラメーターで見事に円弧を近似できることは驚きである。たかが1000x1000ドット以下で表示された、1方向にしか曲がらない曲線だから、4つのパラメーターがある3次曲線なら大概近似できるのだろうかと思って試してみたが、まずうまくいかない。
例えば、曲線をy(x)=ax3+bx2+cx+dで近似することを考える。上と同じように、y(0)=1, y(1)=0, y(cos π/4)=sin π/4, y'(0)=0という条件を与えると、a=-√2, b=√2-1, c=0, d=1となるが、そのグラフを円弧と比較すると、次の図のようにかなりずれが生じる。
(svg only)
y'(0)=0という条件が厳しすぎるのかと思って、y'(cos π/4)=-1に変えても、円弧には近づかない。
(svg only)
円弧の式y=√(1-x^2)をテーラー展開した式
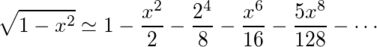
\sqrt{1-x^2} \simeq 1-\frac{x^2}{2}-\frac{2^4}{8}-\frac{x^6}{16}-\frac{5x^8}{128}-\cdots
の8乗の項まで使っても
(svg only)
これくらいずれるのである。3次ベジエ曲線による円弧の近似がいかにミラクルであるかを思い知った。

今回使ったMaximaの入力

f(x):=a*x^3+b*x^2+c*x+d;
define(ff(x),diff(f(x),x)); /* f'(x) */
sol1:solve([f(0)=1,f(1)=0,f(sin(%pi/4))=cos(%pi/4),ff(0)=0],[a,b,c,d]);
sol2:solve([f(0)=1,f(1)=0,f(sin(%pi/4))=cos(%pi/4),ff(sin(%pi/4))=-1],[a,b,c,d]);
plot2d([f(x),sqrt(1-x^2)],[x,0,1.1],[y,0,1.1],[gnuplot_term,"svg"],[gnuplot_out_file,"~/tmp/sol1.svg"]),sol1;
plot2d([f(x),sqrt(1-x^2)],[x,0,1.1],[y,0,1.1],[gnuplot_term,"svg"],[gnuplot_out_file,"~/tmp/sol2.svg"]),sol2;
※define()を使ってるのは、diff()の結果がxの関数と解釈されず、ff(x):=diff(...)とできないため。