乗除を使わずに円を描く

三角関数や平方根はもちろん、×や÷をも使わずに円を描くアルゴリズムがあることを知った。通称ブレゼンハムのアルゴリズム(Bresenham's circle algorithm)と呼ばれるらしい。

さぞかし恐ろしく複雑な反復演算をするんだろう、乗除を使った方が速いというオチではないか、と思いながらウェブ上で調べてみると、どのサンプルコードを見てもとてもシンプルだった。ここ（「伝説のお茶の間」）とかここ（Wikipedia（英語））とかに図解入りの説明とサンプルコードがある。これは速そうだ。

それらのページの図を見て基本的な原理はすぐに理解できたが、説明とソースコードが理解できなかったので、自分で考えてみた。
・Javaのデモページへのリンク
・ソースコード

基本的な原理は、例えば格子上のXY平面（X座標とY座標は整数のみ）で(x,y)=(r,0)の点から45°分の円弧を描く場合、同じY座標でX軸方向に複数の点を描く必要は無いので、yを1ずつ動かしながら、適当な時にxを1つ動かして、点を描いていけば良い。45°分の円弧が描ければ、そのX軸対称、Y軸対称や90°回転を使って360°分の円弧が作れる。

yを+1していく時、いつxを-1すれば良いだろうか。
円の式はx2+y2=r2であるが、x,y,rを整数に限ると、もちろんこの等式は成立せず、なるべく誤差の小さいxを選んでいくことになる。ここでは左辺と右辺の差e(x,y)=x2+y2-r2を誤差として考える。
仮にyを固定してxを-1すると、誤差は(x-1)2+y2-r2になるので、誤差の差分は2x-1である。つまり、誤差eが2x-1より大きい時は、xを-1してもまだ(x,y)は円の外側なので、xを-1する必要がある。
yが1増えるとeが2y+1増えるので、eに2y+1を足していって2x-1を超えればxを-1すれば良い、と考えられる。そう考えてとりあえず書いたのがサンプルコードのmethod1()である。

なるほど、こういう手があったか。
要領が解ったので、もう少し真剣に考えてみる。

上の方法では点が外側に行き過ぎないようにしてるだけなので、円の内側に点を取った方が円弧に近い場合も、円弧より遠い外側の点を取ってしまう。
そこで、次に(x,y)と(x-1,y)の中点が円弧の内側にあるか外側にあるかで点を選ぶことが考えられる。そのためには、円弧とその中点との誤差e(x,y)=(x-1/2)2-y2-r2が正か負かを判定すれば良い。
このeはyが+1すれば2y+1増え、xが-1すれば2x-2減る。(r,0)から始めると初期値が-r+1/4なので、eは整数にならない。従って、e=0になることはなく、e>0かe<0である。yを+1していって、e>0の時は中点が円の外側にあるから、内側の点(x-1,y)を取れば（xを-1すれば）良く、逆にe<0の時は外側の点(x,y)を取れば（xをそのままにすれば）良い。
ということで書いたのが、サンプルコードのmethod2()である。
なお、このコードは上記のWikipediaにあるコード（通称Bresenham's circle algorithm）と意味的にはほぼ同じであり、全く同じ円を描くことを確認した。


MSXを使っていた頃、マシン語で書いてもSIN()やCOS()や乗除が遅いのに対して、BASICのCIRCLE文の円てどうやってこんなに速く描いてるんだろう、と不思議に思っていたものだが、内部でこういうのが動いてたんだなと思うと、感慨深い。

そういえば、もし加減乗除が使えるとしたら、普通どのようにして円を描くのだろうか。と考えてみると、意外に思いつかなかった。

しばらく考えてやっと思いついたのが、三角関数をテーラー展開する方法だった。
円の式を
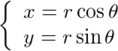
\left\{ \begin{array}{l} x = r \cos\theta \\ y = r \sin\theta \end{array} \right.
とする。このcosθとsinθをTaylor展開すると、
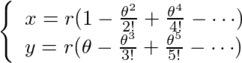
\left\{ \begin{array}{l} x = r(1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \cdots) \\ y = r(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots) \end{array} \right.
が得られる。r<1000、0<t<π/4だと、無限級数部分は3項目までで十分収束する。
円弧の1/8を描くには、このθを0°～45°まで動かせばよいのだが、どれくらいの間隔でθを増やしていけば良いかが問題だ。あまり大きいと円弧が欠けてしまう。
x,yの内、動きが大きいのはyであり、yの動きが最も大きいのは0°近辺である。そのyの増分が1以下であれば、点と点が繋がる。
0°近辺では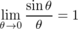\lim_{\theta\rightarrow 0} \frac{\sin\theta}{\theta} = 1、すなわちsinθ≒θなので、y≒rθの増分が1以下であるためには、θの増分が1/r以下であれば良い。
ということで書いたのが、サンプルコードのmethod0a()である。（浮動小数点を使わず、無理やり32bit整数で計算するようにした）


さらに、三角関数を手でTaylor展開しててふと思ったのが、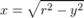x=\sqrt{r^2-y^2}の右辺はyでTaylor展開するとどうなるだろうか、ということだ。しかし、これは私には手では展開できなかった。
後に、Maximaというフリーの数学ソフトに解かせて
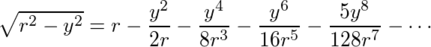
\sqrt{r^2-y^2} = r - \frac{y^2}{2r} - \frac{y^4}{8r^3} - \frac{y^6}{16r^5} - \frac{5y^8}{128r^7} - \cdots
を得た。
幸いにして、y<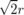\sqrt{2}r<1000くらいだと4項目までで誤差は1以下になる。これを使って書いたのが、サンプルコードのmethod0b()である。
しかし、実際に円を描かせてみると、見てわかるくらいにいびつになった。45°近くが出っ張ってるので、xの減らしが甘いという感じである。何が悪いのだろう？


このサンプルコードは5つの同心円を描くが、内側から順に、
・Javaの円描画メソッド(Graphics#drawArc)で描いた円
・１つ目の方法で描いた円
・２つ目の方法（ブレゼンハムのアルゴリズム）で描いた円
・三角関数をTaylor展開して描いた円
・xをyでTaylor展開して描いた円
である。2番目は上述のように真円からの誤差が大きく、4番目は計算量が大きく、5番目はいびつで論外である。ブレゼンハムのアルゴリズムは秀逸だ。


ところで、直線を描くアルゴリズムでDDA(Digital Differential Analyzer)と呼ばれるものがあるが、ブレゼンハムのアルゴリズムみたいなのはDDAとは呼べないのだろうか？

その他参考リンク：
Comparing Circle Drawing Algorithms [openfmi]