偏相関係数の式の導出をやってみた

偏相関係数とは、XとZ、YとZに相関がある時の、Zの影響を抜いたXとYの相関係数である。XとYの相関係数の絶対値が大きくても、それぞれが間接的な要因Zと因果関係がある場合、それによって相関が強くなっている可能性がある。

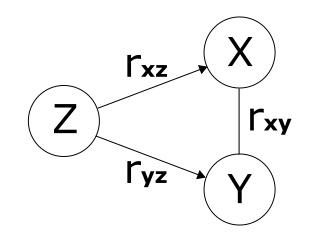
そのような場合に、Zの影響を除いたXとYの相関係数を知りたくなる。
相関係数が高いが実はXとYに因果関係が無く、それぞれ間接的な要因Zと因果関係がある疑似相関（見せかけの相関関係）の例としては、アイスクリームの売上と水難事故の発生数の相関（気温が間接要因）や、警察官の人数と犯罪の発生数の相関（人口が間接要因）などが知られているようで、筆者も何度も聞いた覚え、見た覚えがある。

XとY、XとZ、YとZの相関係数をそれぞれrxy, rxz, ryzと書くと、Zの影響を除いたXとYの偏相関係数rxy⋅zは次の式で表される、と色々な所に書いてある。
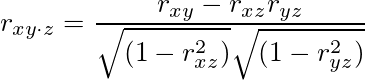
r_{xy\cdot z}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{\vphantom{r_{yz}^2}(1-r_{xz}^2)}\sqrt{(1-r_{yz}^2)}}

何故こうなるのだろうと思って、筆者が30年前に通っていた時の大学の教科書を読み返したら、「簡単な計算により（上の式）を得る。」とだけ書かれていて、導出過程が載っていなかった。
しかし、その上に考え方は書いてあったので、そこから計算してみた。
いくつか前提知識の復習が必要で、やり始めると面倒くさそうで気が削がれるが、一踏ん張りすれば、確かに簡単だった。

考え方としては、X,YをそれぞれZの一次関数として回帰すると、それらのZの項がZの影響の部分なので、それぞれのZの項の部分を抜いたもの同士の相関係数を偏相関係数とするということらしい。定数項を抜いても相関係数は変わらないので、X,Yそれぞれの残差同士の相関係数ということになる。

以下、Xの標本をxi 、Xの標本標準偏差をsx 、XとYの標本共分散をsxy 、XとYの標本相関係数をrxyのように表記する。
XをZで一次回帰すると
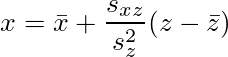
x=\bar{x}+\frac{s_{xz}}{s_z^2}(z-\bar{z})
となることから、X,YをZで回帰した時の残差X',Y'は次のようになる。
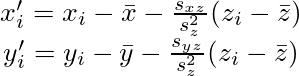
\matrix{ x'_i=x_i-\bar{x}-\frac{s_{xz}}{s_z^2}(z_i-\bar{z}) \cr y'_i=y_i-\bar{y}-\frac{s_{yz}}{s_z^2}(z_i-\bar{z}) }
求めるものは、相関係数の定義より
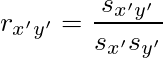
r_{x'y'}=\frac{s_{x'y'}}{s_{x'}s_{y'}}
である。このsx'y', sx', sy'をそれぞれ計算していく。
共分散の定義より、
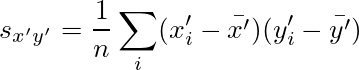
s_{x'y'}=\frac{1}{n}\sum_i(x'_i-\bar{x'})(y'_i-\bar{y'})
であり、一次回帰式の誤差はN(0,σ2 )に従う前提（最小二乗推定量の最小分散性は正規性を仮定している）であることから、X'とY'の平均は0なので、
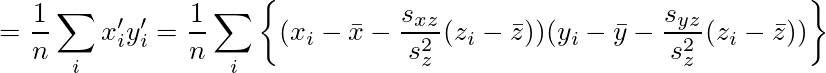
= \frac{1}{n}\sum_i x'_iy'_i = \frac{1}{n}\sum_i\left\{(x_i-\bar{x}-\frac{s_{xz}}{s_z^2}(z_i-\bar{z}))(y_i-\bar{y}-\frac{s_{yz}}{s_z^2}(z_i-\bar{z}))\right\}
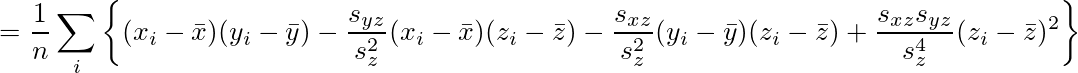
= \frac{1}{n}\sum_i\left\{ (x_i-\bar{x})(y_i-\bar{y})-\frac{s_{yz}}{s_z^2}(x_i-\bar{x})(z_i-\bar{z})-\frac{s_{xz}}{s_z^2}(y_i-\bar{y})(z_i-\bar{z})+\frac{s_{xz}s_{yz}}{s_z^4}(z_i-\bar{z})^2 \right\}
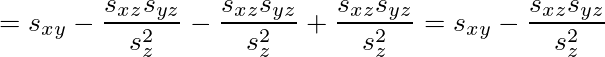
=s_{xy}-\frac{s_{xz}s_{yz}}{s_z^2}-\frac{s_{xz}s_{yz}}{s_z^2}+\frac{s_{xz}s_{yz}}{s_z^2}=s_{xy}-\frac{s_{xz}s_{yz}}{s_z^2}
sxy=sxsyrxyなので
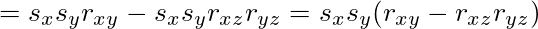
=s_xs_yr_{xy}-s_xs_yr_{xz}r_{yz}=s_xs_y(r_{xy}-r_{xz}r_{yz})
となる。同じ要領で、
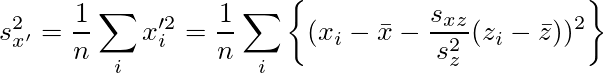
s_{x'}^2=\frac{1}{n}\sum_i x'^2_i=\frac{1}{n}\sum_i \left\{(x_i-\bar{x}-\frac{s_{xz}}{s_z^2}(z_i-\bar{z}))^2\right\}
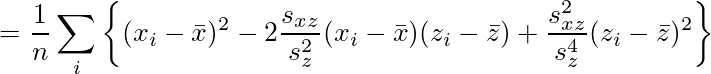
=\frac{1}{n}\sum_i \left\{(x_i-\bar{x})^2-2\frac{s_{xz}}{s_z^2}(x_i-\bar{x})(z_i-\bar{z})+ \frac{s_{xz}^2}{s_z^4}(z_i-\bar{z})^2\right\}
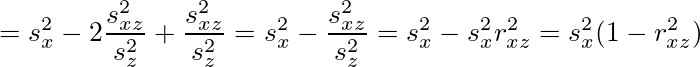
=s_{x}^2-2\frac{s_{xz}^2}{s_z^2}+\frac{s_{xz}^2}{s_z^2}=s_{x}^2-\frac{s_{xz}^2}{s_z^2}=s_{x}^2-s_{x}^2r_{xz}^2=s_{x}^2(1-r_{xz}^2)
となる。sy'についてはxとyを入れ替えただけなので省略する。従って、
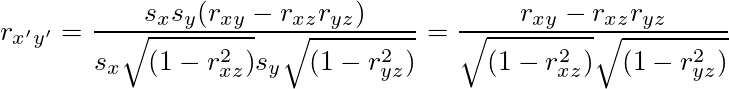
r_{x'y'}=\frac{s_xs_y(r_{xy}-r_{xz}r_{yz})}{s_x\sqrt{\vphantom{r_{yz}^2}(1-r_{xz}^2)} s_{y}\sqrt{(1-r_{yz}^2)}}=\frac{r_{xy}-r_{xz}r_{yz}}{\sqrt{\vphantom{r_{yz}^2}(1-r_{xz}^2)} \sqrt{(1-r_{yz}^2)}}
である。

この偏相関係数の式を変形して
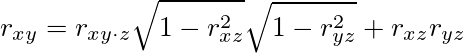
r_{xy}=r_{xy\cdot z}\sqrt{\vphantom{r_{yz}^2}1-r_{xz}^2}\sqrt{1-r_{yz}^2}+r_{xz}r_{yz}
とすると、rxzとryzが大きければrxyに大きく影響し、rxy⋅zと符号が逆になることも容易に起こることが想像できる。XとYが無相関(rxy⋅z=0)でも、例えばrxz=ryz=0.8だとrxy=0.64であり、かなり強い相関が観測されることになる。相関係数には疑似相関の影響大である。