カルマンフィルターの例題として、何らかの物理的な物体があり、内部状態として位置xと速度vがあり、それぞれがノイズの影響を受け、観測できるのはxに観測誤差を加えたzのみとし、位置xを一定の目標値に制御したいとする。
次のコードのPhysicalModelを制御対象とする。xを取得するメソッドがあるが、制御する際に観測できるのはzだけであり、xの本当の値は観測できないとする。
import numpy as np
import matplotlib.pyplot as plt
class PhysicalModel(object):
x_std = 1.0 # 位置xのノイズの標準偏差
v_std = 0.5 # 速度vのノイズの標準偏差
z_std = 2.0 # xの観測誤差の標準偏差
def __init__(self, timesteps, init_x, init_v, random_seed=1):
np.random.seed(random_seed)
self.x = np.zeros(timesteps) # 位置x(便宜上過去の値を保存)
self.v = np.zeros(timesteps) # 速度v
self.a = np.zeros(timesteps) # 加速度a
self.z = np.zeros(timesteps) # xの観測値z
# t=0
self.t = 0 # 時刻
self.x[0] = init_x
self.v[0] = init_v
self.z[0] = self.x[0]
# 時刻tを1つ進める
def step(self):
self.t += 1
self.x[t] = self.x[t-1] + 0.99 * self.v[t-1] + 1/2 * self.a[t-1] + self.x_std * np.random.randn(1)[0]
self.v[t] = 0.98 * self.v[t-1] + self.a[t-1] + self.v_std * np.random.randn(1)[0]
self.z[t] = self.x[t] + self.z_std * np.random.randn(1)[0]
return self.z[t] # 1つ進めた時刻の観測値を返す
# 時刻tの加速度を入力する
def set_accel(self, a):
self.a[t] = min(10, max(-10, a)) # 実際には -10 <= a <= 10 に制限されるとする
# t=offset以降のxの目標値からの平均二乗誤差
def MSE(self, mean, offset=0):
return sum((self.x[offset:] - x_target) ** 2) / self.x[offset:].shape[0]
# グラフ表示用
def get_x_history(self):
return self.x[:t+1]
def get_v_history(self):
return self.v[:t+1]
def get_a_history(self):
return self.a[:t+1]
def get_z_history(self):
return self.z[:t+1]
まず、カルマンフィルターを用いず、観測値zを使って制御してみる。
xの初期値は20、目標値は5とする。
制御入力は、ノイズやvの減衰を無視すると
xt+1 = xt + vt + (1/2) at
なので
at = 2 (xt+1 - (xt + vt))
であり、次の時刻(t+1)で目標値に到達させるなら
at = 2 (x_target - (xt + vt))
だが、観測値zから推測したx,vはノイズを含むので、その影響を小さくする為、入力するaは上の式の半分とする。(実際、上の式の2を色々変えてみても1.0前後くらいが良さそうだった。時刻(t+2)で目標値に到達させるべく、
xt+2 = xt + 2vt + 2 atから
at = (1/2) (x_target - (xt + 2vt))
とするのも有効そうだったが、今回は単純な例で試す。)
timesteps = 50
init_x = 20
x_target = 5
model = PhysicalModel(timesteps, init_x=init_x, init_v=0)
estimated_v = [0] # vの推定値、グラフ表示用に保存する
z_prev = init_x # t=0の観測値
a = 0 # t=0の加速度
for t in range(1, timesteps):
z = model.step()
# x,vの推定
# z = z_prev + v_prev + a/2
# v = v_prev + a
# -> v = z - z_prev - a/2 + a
x = z
v = z - z_prev + a/2
estimated_v.append(v)
# 制御入力
a = 1.0 * (x_target - (x + v))
model.set_accel(a)
z_prev = z
print("MSE =", model.MSE(x_target, offset=10))
fig = plt.figure(figsize=(10,4))
ax1 = fig.gca()
ax2 = ax1.twinx()
ax1.plot(model.get_z_history(), label='observed')
ax1.plot(model.get_x_history(), color='r', linewidth=2, label='true_x')
ax2.plot(model.get_v_history(), 'y', alpha=0.5, label='true_v')
ax2.plot(estimated_v, 'y', linestyle='--', label='estimated_v')
ax1.grid(axis='y')
ax1.set_ylim((-2, 22))
ax1.set_xlabel('time')
ax1.set_ylabel('x')
ax2.set_ylabel('v')
ax1.legend(loc='upper right', bbox_to_anchor=(1, 0.7))
ax2.legend(loc='upper right')
ax1.set_title("Controlling x to 5")
plt.show()
# 別の制御方式との比較用
true_x_1 = model.get_x_history()

MSE = 5.654622082289254
赤線が制御対象のxである。一応、xが5辺りに制御されている。
次に、カルマンフィルターを用いてx,vを推定しながら制御してみる。
制御対象を状態空間モデルで表すと、このようになる。
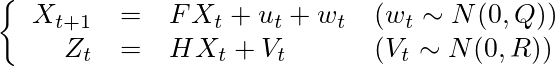
上の式が状態方程式、下の式が観測方程式と呼ばれるものである。
ここでのXは位置xと速度vを含む状態ベクトル、
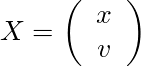
であり、時刻tからt+1の間にシステム行列Fによる状態遷移と、制御入力uと、平均0、分散Qの多変量正規分布に従うノイズwが加わるとする。
Zは状態Xの観測値で、Xが観測行列Hにより変換され、平均0、分散Rの多変量正規分布に従うノイズVが加わるとする。(このVは小文字のvで表記されることが多いが、今回の例では速度のvと紛らわしいので、ここでは大文字で記す)
制御入力uは加速度aにより、vの減衰を無視すると、ノイズを除いた部分は
xt+1 = xt + vt + (1/2) at
vt+1 = vt + at
となるので、
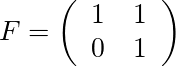
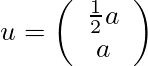
となる。
状態はxしか観測できないので、観測行列Hは[1 0]となる。
Q,Rは最小二乗法で推定する方法があるらしいが、今回は経験的にこれくらいだと知っているものとして、それぞれ[[1, 0], [0, 0.1]]と[5]とする。
次のコードはpykalmanを用いた例である。
●コード
# pykalmanのカルマンフィルターを使う例
from pykalman import KalmanFilter
model = PhysicalModel(timesteps, init_x=init_x, init_v=0)
kf = KalmanFilter(
transition_matrices=[[1, 1], [0, 1]],
observation_matrices=[1, 0],
transition_covariance=[[1, 0], [0, 0.1]],
observation_covariance=[5],
# initial_state_mean=[init_x, 0], # 今回の使い方では関係無かった
# initial_state_covariance=[[0, 0], [0, 0]] # 何にしても変わらない
)
filtered_state = np.zeros((timesteps, 2)) # x,vの推定値、グラフ表示用に保存する
filtered_state[0] = [init_x, 0]
filtered_state_cov = np.zeros((timesteps, 2, 2)) # x,vの推定値の分散
a = 0 # t=0の加速度
for t in range(1, timesteps):
z = model.step()
# x,vの推定
filtered_state[t], filtered_state_cov[t] = kf.filter_update(
filtered_state[t-1],
filtered_state_cov[t-1],
z,
transition_offset=np.array([1/2 * a, a])
)
x, v = filtered_state[t]
# 制御入力
a = 1.0 * (x_target - (x + v))
model.set_accel(a)
print("MSE =", model.MSE(x_target, offset=10))
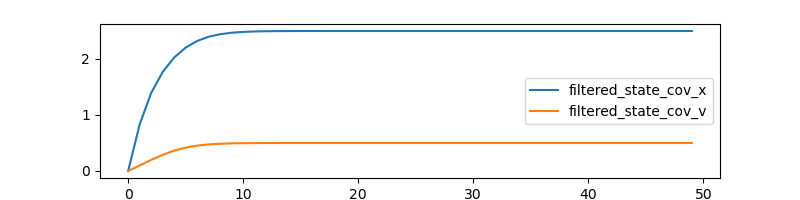
# 安定確認
plt.figure(figsize=(8,2))
plt.plot(filtered_state_cov[:,0,0], label='filtered_state_cov_x')
plt.plot(filtered_state_cov[:,1,1], label='filtered_state_cov_v')
plt.legend()
plt.show()
fig = plt.figure(figsize=(10,4))
ax1 = fig.gca()
ax2 = ax1.twinx()
ax1.plot(model.get_z_history(), label='observed')
ax1.plot(filtered_state[:,0], linestyle='--', label='filtered_x')
ax1.plot(true_x_1, color='r', alpha=0.3, label='true_x(prev)')
ax1.plot(model.get_x_history(), color='r', linewidth=2, label='true_x')
ax2.plot(model.get_v_history(), 'y', alpha=0.5, label='true_v')
ax2.plot(filtered_state[:,1], 'y', linestyle='--', label='filtered_v')
ax1.grid(axis='y')
ax1.set_ylim((-2, 22))
ax1.set_xlabel('time')
ax1.set_ylabel('x')
ax2.set_ylabel('v')
ax1.legend(loc='upper right', bbox_to_anchor=(1, 0.7))
ax2.legend(loc='upper right')
ax1.set_title("Controlling x to 5")
plt.show()
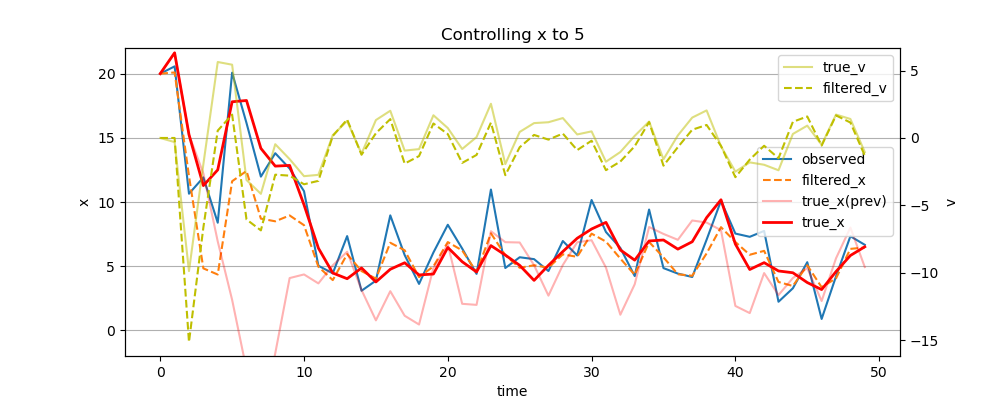
MSE = 3.238811619518345
濃い赤線が制御対象のx、青線が観測値、オレンジの点線がxの推測値である。全体的には推定値が観測値より本当のxに近いように見える。薄い赤線が上のカルマンフィルターを使わない例のxであり、何となく、今回の方がよりx=5の近くに制御されているように見える。また、黄色の実線が本当のv、黄色の点線が推測したvであり、観測していないvがそれにりに正しく推測され、本当のvも0付近で安定している。
出力のt≧10のMSEで見ても、誤差が小さくなっている。
